女士們,先生們,老少爺們兒們!在下張大少。
印度南部的一種圖畫傳統表達了數學思想,並引起了計算機科學的注意
在印度東南部泰米爾納德邦,婦女每天早上清掃門庭,用牛糞水灑在門庭上,然後用米粉在門庭上繪製精緻、對稱的圖案。他們用中指和食指夾住米粉,用拇指引導米粉的流動。根據傳統,牛糞可以清潔地面,而使用米粉則是為螞蟻和其他昆蟲提供食物,以此來開始一天的善舉。女孩從她們的女性親戚那裡學習這種kolam傳統,kolam技能被視為優雅的標誌,也是靈巧、精神紀律和集中能力的表現。在泰米爾納德邦的房屋門庭上,每天都有各種各樣的kolam設計,從多個角度吸引了人們的注意。除了它們在泰米爾文化中的意義之外,它們還是在文化環境中表達數學思想的一個不尋常的例子。此外,近年來,kolam圖案吸引了對使用圖片語言分析和描述影象感興趣的計算機科學家的注意。
我自己的研究重點是探索數學思想的不同表達方式和文化背景。作為對現代數學歷史發展的補充,這些研究關注那些沒有被視為數學主流的口頭傳統和文化。作為一個指導性的定義,我認為數學思想是那些涉及數字、邏輯、空間配置,以及更重要的,將這些思想組織成系統和結構的思想。特別值得關注的是,人們自己將這些思想視為重要的知識,需要仔細學習並小心翼翼地傳承下去的情況。
以相互排斥的語言社群為標準,在過去的700年裡至少有6000種不同的文化存在。要尋找屬於口頭傳統的數學思想,往往需要從數學角度重新審視人類學家、考古學家、語言學家和文化歷史學家的工作和材料。數學思想的許多文化背景包括記錄、日曆製作、建築、裝飾、導航、親屬組織、繪圖、占卜和宗教。從本質上講,時間和空間的概念以及自然、超自然和社會世界的秩序都可能涉及數學思想。例如,印加人開發了一種涉及數字邏輯系統的記錄方法,使用彩色結繩的陣列;在馬紹爾群島人民的導航傳統中,用椰子纖維捆綁的棕櫚肋骨製成的二維結構作為他們對波浪和陸地的相互作用的概念的平面表示;馬達加斯加的占卜依賴於使用涉及雙值邏輯的複雜代數演算法佈置種子的陣列。
Kolam傳統與我所研究的其他案例不同的是,它直接促進了一項學術工作。複雜的圖案進入了計算機科學領域。這些圖案為說明分析和描述圖片的已知方法提供了材料,也激發了新的方法。這使得kolam傳統成為一個罕見且特別有趣的案例。
Kolam圖案
泰米爾納德邦的kolam傳統延續了數百年,在城市和農村地區的婦女中仍然是一種普遍做法,無論是受過大學教育的婦女還是受教育程度較低的婦女都是如此。最近幾年,女性經常用市面上可以買到的石粉、粉筆或墨水代替大米來創作這些設計,從泰米爾納德邦移民過來的女性通常會在新家繼續這種做法。
圖1。在泰米爾納德邦,母親教女兒如何繪製裝飾門庭的kolam圖案。學習畫kolam圖案是女孩成長過程中的一個重要部分,已經有幾百年的歷史了。近幾十年來,這一傳統吸引了對使用圖片語言分析和描述圖片感興趣的計算機科學家的注意。作者長期以來一直在研究跨文化數學思想的表達,他描述了kolam傳統是如何對現代計算機科學做出貢獻的。
每天在門庭上放置圖案是泰米爾文化的一個重要組成部分。裝飾過的圖案是內部世界和外部世界的分界線,圖案既可以守護家庭,又可以歡迎來訪者。婦女們教女孩們一系列的圖案和繪製程式,以及哪些圖案適合於日常使用,哪些圖案適合於特殊場合或特定儀式和節日。學習kolam傳統是女孩成長過程中的一個重要部分。儘管繪製kolam圖案是一種從母親傳給女兒的口頭傳統,但它是一種在識字文化內的口頭傳統。事實上,泰米爾人有書面文字和大量的文學作品,最早可以追溯到公元前三或四世紀。然而,泰米爾文學作品只是順便提到了kolam傳統,包括很少的細節。不過,這些文獻還是證明了這一傳統的長久性和普遍性。例如,已知最早的參考文獻之一,即16世紀的著作,講述了一個和平且繁榮的王國,其中 "老虎和牛在同一個地方喝水,婆羅門誦讀吠陀經,婦女用kolam裝飾街道,雨水如期而至,飢餓的人得到食物"。
在印度泰米爾納德邦以外的部分地區,也有類似的繪畫傳統,其中有muggu、rangoli和alpana。雖然這些傳統可能是有歷史聯絡的,但這些圖形是不同的,因為它們的含義和繪製它們的程式也是不同的。最近,一些傳統已經擴充套件到包括其他傳統的各個方面;因此,有時它們的術語可以互換使用。在這篇文章中,我只考慮傳統形式的kolam設計,即只由白線組成的圖形,或由白線和點組成的圖形,有時被認為類似於網、迷宮或金銀絲。
因為這種做法是隨著泰米爾納德邦移民而來的,例如,在19世紀末從泰米爾納德邦移民到斯里蘭卡的茶園工人中,以及那些移民到美國的人中,可以找到kolam的傳統。這一傳統與泰米爾納德邦人民的價值觀、儀式和哲學深深交織在一起,成為泰米爾文化的標誌。例如,這可以從選擇Kolam作為致力於泰米爾研究的國際學術期刊的標題中看出。
許多但不是所有的kolam繪圖都是從放置點網格開始的。除了其他排列之外,這些點可以形成矩形、三角形或六邊形陣列,或者從中心點輻射。然後透過連線點或圍繞點畫出圖形,點既引導又約束圖形。對於一些kolam,可能以點的網格開始,也可能不以點的網格開始,重要的是用一條連續的線畫出每個圖形,從它開始的地方結束。這些封閉的、連續的圖案,以及由一些這樣的封閉線組成的其他圖案,與生、育、死的永無止境的迴圈,與連續性、整體性和永恆性的概念相關聯。
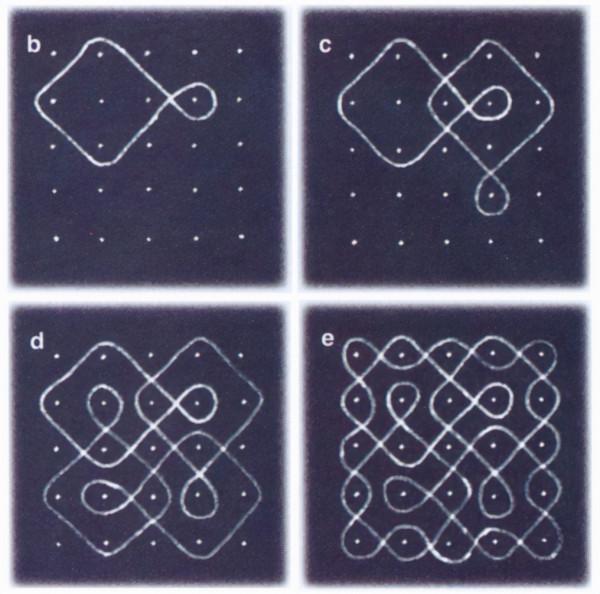
圖2. kolam圖案在風格上差異很大。所有這些例子都是從一個點的網格開始的;圖案a、b和c是把點連線起來,而d、e和f則是曲線則圍繞著點。婦女畫的圖案c、e和f是封閉的連續曲線。觀察者注意到,d不是連續畫的,儘管它可以用一條封閉的曲線來畫。注意圖案中不同種類的對稱----圍繞水平中心線的對稱,圍繞垂直中心線的對稱和圍繞中心點45度(c)、90度(d)和180度(e)的旋轉對稱。
觀察發現,一些可以畫成閉合連續曲線的圖形實際上並不是在一次連續掃掠中畫出來的。例如,圖3說明了一種這樣的情況;kolam是使用基本單位的系統變換繪製的。該圖將基本單位重複四次,每個單位相對於前一個單位旋轉90度。最後,另一條連續的閉合曲線圍繞著這四個單元。總體而言,kolam圖案顯示了對於對稱性的關注。圖形顯示出圍繞水平線、垂直線或各種旋轉對稱的對稱性。
圖3。許多但不是所有的kolam繪畫都是從建立一個點的網格開始的,這個網格預示了圖形(a)的最終大小和形狀。女孩們學習規定的方法來畫許多圖形。為了繪製圖2d中所示的單元,一個基本單元被繪製4次,其中每個單元相對於它之前的單元旋轉90度(b,c,d),並且一條連續的曲線最終將四個單元包圍在內部(e)。
一些kolam圖案構成了系列;也就是說,有一些具有共同特徵的圖組。在某些情況下,一個系列中較大的圖案是由較小的圖案的幾個副本組成的;在其他情況下,系列成員是以更微妙的方式相互衍生的。Kolam圖形系列的概念和組織似乎特別能表達數學思想。
圖片語言
歸類為系列的kolam圖形特別吸引了理論計算機科學家的興趣。理論計算機科學家關注的是透過使用圖片語言來分析和描述圖片,圖片語言使用基本單元的集合和具體的正式規則來組合這些單元。對圖片語言的研究類似於形式語言理論,它始於大約45年前諾姆·喬姆斯基(Noam Chomsky)對自然語言的研究。在隨後的幾十年裡,計算機科學家們將形式語言理論用於分析和規範程式語言。
來自泰米爾納德邦Madras基督教學院的Gift Siromoney,首次將kolam設計用於圖片語言的研究。1989年,為了紀念他的一生,人們出版了一卷文獻,其中列出了Gift Siromoney出版的大約100本著作,這些著作展示了他一生中將自己的學術興趣與對泰米爾納德邦環境、歷史和文化的深切關注結合在一起的多種方式。Gift Siromoney和他的妻子以及其他計算機科學家,特別是Kamala Krithivasan和k . g . Subra manian, kolam設計成為一個豐富的資料,可以作為一些現有型別的語言和圖片的例子也作為刺激的建立新型別的語言。除了Madras小組,其他計算機科學家也使用圖片語言來描述kolam系列。
在這裡,我將描述用於製作一些kolam系列的圖片語言。作為開胃菜,讓我們看看一個產生符號串的初級形式語言的例子,然後看看這樣的符號串如何被翻譯成圖片。假設我們的語言中的符號被限制為A、B、C,並且起始字串是ABAA。我們從以前的字串中建立一個新的符號串的規則是:
B->AC, A->B, C->CC.
我們把對前一個字串應用這些改寫規則而產生的字串稱為結果。因此,如果開始的字串是ABAA,第一個結果就是BACBB,第二個結果就是ACBCCACAC,第三個結果就是BCCACCCBCCBCC。改寫規則可以繼續產生肯定的結果。在每個階段,三個規則同時應用(也就是平行應用)而不是順序應用,因此,例如,在某個階段透過應用規則B->AC引入的A和C一直到後面的階段都沒有被修改。這是林登邁爾語言的特點,或稱L語言,它以對植物生長建模感興趣的生物學家阿里斯蒂德-林登邁爾(Aristid Lindenmayer)命名。在我們的例子中,該語言是一種上下文無關、確定性的L-語言。它是無語境的,因為每個符號的命運都是單獨處理的,不參考相鄰的符號;它是確定性的,因為每個符號只有一個可能的重寫規則。
現在的問題是如何從一個符號串中建立一幅圖片。Przemsylaw Prusinkiewicz在L系統的計算機圖形學應用方面特別引人注目,他開發了使用解釋為“海龜命令”的符號的技術。海龜圖形是Seymour Papert在20世紀60年代的想法;他構思這種語言主要是為了透過使用計算機培養兒童的想象力。這個想法是:烏龜可以透過拖動它的尾巴來畫出一個影象。或者它可以抬起它的尾巴,創造一個不連續的圖畫。烏龜沒有整體視角,但它可以透過理解和執行一組有限的命令來創造複雜的圖畫,這些命令是由一組符號傳達給它的。這些命令包括
F:在畫線的同時向前移動一步。
f: 在不畫線的情況下向前移動一步。
+: 左轉(逆時針),角度為d。
-: 右轉(順時針),角度為d。
每幅畫都必須從指定烏龜的方向和角度d開始,這在整幅畫中保持不變。每一步都從上一步結束的地方和方向開始。例如,具有海龜解釋的上下文無關、確定性的L語言可以重現Kolam圖的Snake系列(圖5)。連續繪製,並在開始的地方結束,蛇形kolam與許多其他kolam的不同之處在於,在它的繪製之前沒有圓點。海龜對它的解釋使用了直線,併產生了設計的角度版本,儘管結合數學資料擬合技術可以生成平滑的曲線。在任何情況下,描述角蛇的語言首先將d定義為45度,並以B--F--B--F作為起始字串。海龜總是解釋為表示F+F+F--F--F+F+F,生成更復雜的Snake圖形的重寫規則是B->B+F+B--F--B+F+B。圖5顯示了B、起始字串以及第一和第二個結果的圖形表示。重寫規則的連續應用導致設計呈指數增長。展示的最複雜的蛇形kolam是第三種結果的平滑版本。如果我們減小海龜每次出來的腳步的大小,這樣連續的圖畫就可以放在一個相同大小的正方形中,如果我們無限期地繼續下去,我們將得到一個令人驚訝的結果,即所謂的謝爾賓斯基曲線,它是以1912年描述它的數學家的名字命名的,這種填充空間的自迴避分形被稱為謝爾賓斯基曲線。
圖5.圖片語言可以建立名為Snake的kolam型別的角度版本。最小的圖案顯示起始字串B--F--B--F,其中F表示向前移動一步,-表示順時針移動45度,+表示逆時針移動45度,表示F+F+F--F--F+F+F。應用重寫規則B->B+F+B--F--B+F+B會生成更復雜版本的Snake kolam。第一個結果是(B+F+B--F--B+F+B)--F--(B+F+B--F--B+F+B)--F。每次應用重寫規則都會將四臂十字架中的每個臂替換為新的四臂十字架,從而導致數字從4臂到16臂再到64臂呈指數級增長,以此類推。
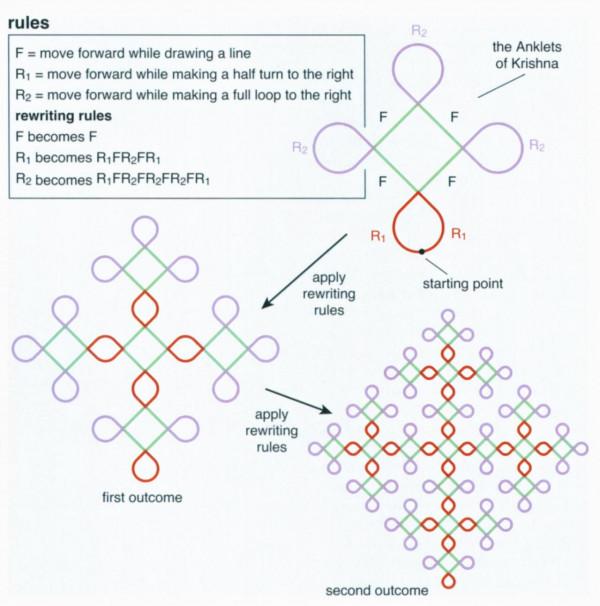
一種無上下文的確定性L語言也被用來描述另一個Kolam系列:克里希納的腳鏈。與蛇形系列一樣,克里希納的腳鏈系列的成員是相互遞迴的,並以指數形式增長。Madras小組的計算機科學家們透過使用他們所謂的 "kolam "動作來繪製平滑的曲線和迴圈,而不是使用線性烏龜動作,從而避免了產生有角度的kolam圖形。Madras小組根據泰米爾婦女對其動作的描述,定義了七個kolam動作。繪製克里希納的腳鏈只需要其中的三個動作:
F:向前移動,同時畫一條線。
R1: 向前移動,同時向右轉半圈。
R2: 向前移動,同時向右做一個完整的迴圈。
一種能產生克里希納的腳鏈的語言,從開始的字串R1FR2FR2FR1開始,並有以下重寫規則。R1->R1FR2FR1和R2->R1FR2FR2FR1(圖6)。就像蛇形圖案一樣,每次應用改寫規則都會用一個新的四臂十字架替換四臂十字架中的每一個臂,越來越複雜的克里希納的小腳板圖案是透過用一組四葉子替換每個小葉子而產生的。有幾個kolam系列以類似的方式成長。
圖6. 一種圖畫語言使用起始字串R1FR2FR2FR2FR1和規定每個符號的含義以及如何改寫字串中的符號以創造越來越複雜的結果的框內規則,在克里希納的腳鏈系列中創造了kolam圖。改寫規則的每一次應用都會將每張小冊子替換成一組四張小冊子。
陣列語言
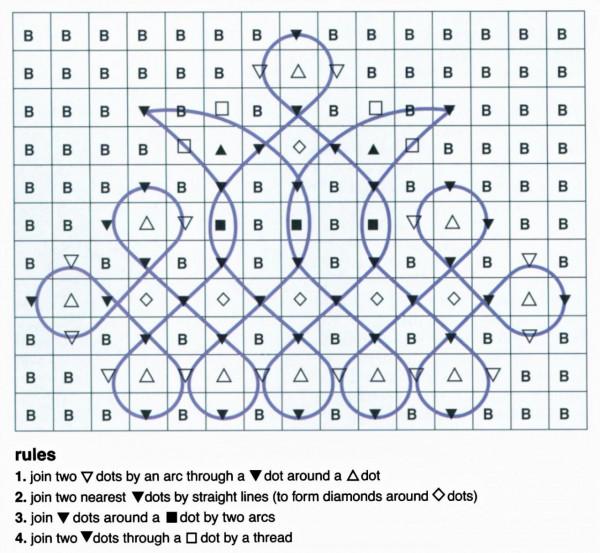
我所描述的圖片語言可以表達一些圖形系列,但是它們忽略了大多數kolam圖形開頭的點陣。泰米爾納德邦婦女在畫kolam之前佈置的點陣預示著每個圖案的最終大小和形狀。或者,換句話說,女性在完成繪畫之前,會用這些點來創造圖案的二維骨架結構。Kolam傳統的這一值得注意的方面促使Madras團隊致力於陣列語法,它處理符號的二維陣列而不是符號串。從符號陣列開始,陣列語言的重寫規則用其他子陣列替換子陣列。但他們必須解決的一個反覆出現的問題是,新引入的子陣可能在形狀或大小上與它們所替換的子陣不同,從而在新陣列中造成形狀扭曲。在被稱為Siromoney矩陣語法的陣列語法中,可以表示圖形單元的簡單變換。例如,這可以應用於圖2a中的kolam系列的生成。同樣的單位在水平方向複製了兩次,垂直方向複製了一次。用另一種kolam來說,基本單位可以在重複時反映出來。另一種型別的語法“kolam array語法”處理圖形的生成,其中圖形的長度和寬度具有固定的關係。Madras小組的重要貢獻在於它們推廣了一些基本的字串運算,以便將它們應用於矩形陣列和六角形陣列。在1986年的一篇文章中,Rani Siromoney提供了Madras小組在陣列語法方面的廣泛工作的全面討論和參考書目;在這篇文章中,她描述了該小組追求的各個方面,以及他們的工作如何與其他人的工作相關。他們的大部分工作涉及他們提出的語言型別的形式性質,而他們的一些著作則將這些語言應用於kolam系列。
Madras小組使用兩種不同的方法對陣列語言生成的符號陣列進行圖形化解釋。一種方法將矩形陣列中的符號解釋為連續的圖形單元。圖形單元的特定集合因語言而異,因為它們依賴於陣列語言描述的kolam系列。要建立kolam系列的各種成員,生成連續陣列的規則必須捕獲給定系列中單元的固有組織。從符號陣列生成圖片的第二種方法更接近泰米爾納德邦婦女用來畫kolam的程式。其中,陣列中的符號可以被認為是點,而是攜帶指導圖形繪製的指令的點。陣列中的點型別及其指令因語言的不同而不同;同樣,它們特定於陣列描述的kolam系列。要建立kolam系列成員,用於生成連續陣列的規則必須捕獲指令點的圖案化組織。圖7和圖8顯示了這兩種不同的方法如何生成山頂kolam圖案。
圖7. 不同的陣列語言可以創造出山頂系列的kolam圖,其增長速度是多項式增長而不是指數增長。在一種語言中,所產生的矩形陣列中的符號被解釋為連續的圖形單元。在右邊,圖形單元被疊加在一個符號陣列上。
圖8. 另一種生成山頂kolam圖系列成員的陣列語言將陣列中的符號解釋為攜帶特定指令的圓點。
Kolam的演算法性質
當計算機科學家試圖用圖片語言來捕捉kolam的圖形時,他們強調了kolam圖形的豐富性和它們的演算法性質——換句話說,它們是以有秩序的、一步一步的方式建立的。這些語言不一定能複製泰米爾納德邦的婦女如何構思和繪製kolam圖。然而,它們強調了這樣一個事實:kolam,特別是kolam的系列,不僅僅是單個圖片的集合;系統的程式和技術使它們統一起來。
kolam傳統也為計算機科學家提供了一個不尋常的機會。可能沒有比將其應用於產生該結構的傳統和文化之外的例子更好的方法來研究一個學術結構。但除此之外,計算機科學家們還試圖從圖案的製造者那裡學習,並將他們所學到的東西整合到他們自己領域的理論和實踐中。kolam傳統歷史的這一最近階段展示了數學思想如何超越其傳統界限,與學術努力互動,並在事實上為其作出貢獻。
毋庸置疑,數學思想蘊含在kolam的傳統中,它強調豐富的對稱性、圖案的重複性、封閉的連續曲線和曲線系列。印度婦女構思和繪製傳統的kolam圖形,並在其中引入變化,但它們仍然是代代相傳的思想庫的一部分。這些圖案是泰米爾納德邦文化環境的重要組成部分——文化中的每個人都能看到、認識和欣賞這些圖案。kolam傳統當然是全球持續不斷的數學思想史的一部分,但最重要的是,它仍然是泰米爾納德邦文化和日常景觀的核心部分。
參考文獻
1 Ascher, M. 1994. Ethnomathematics: A Multicultural View of Mathematical Ideas. New York:Chapman & Hall/CRC.
2 Ascher, M. In press. Mathematics Elsewhere. Princeton, N.J.: Princeton University Press.
3 Ascher, M., and R. Ascher. 1997. Mathematics of the Incas: Code of the Quipu. New York:Dover Publications, Inc. (Reprint of 1981 Code of the Quipu: A Study in Media, Mathematics, and Culture. Ann Arbor: University of Michigan Press.)
4 Durai, H. G. 1929. Preliminary note on geometrical diagrams (kolam) from the Madras Presidency. Man 29:77-78
5 Narasimhan, R. 1989. List of selected publications of Dr. Gift Siromoney. In A Perspective in Theoretical Computer Science: Commemorative Volume for Gift Siromoney, ed. R. Nara simhan. Series in Computer Science, vol. 16. London: World Scientific, pp. xi-xviii.
6 Narasimhan, R. 1992. The oral-literate dimension in Indian culture. In Indological Essays:
Commemorative Volume 11 for Gift Siromoney, ed. M. Lockwood, Department of Statistics, Madras Christian College, pp. 67-79.
7 Prusinkiewicz, P., K. Krithivasan and M. G. Vi jayanarayana. 1989. Application of L-systems to algorithmic generation of South India folk art patterns and Karnatic music. In A Perspective in Computer Science: Commemorative Volume for Gift Siromoney, ed. R. Narasimhan. Computer Science Series, vol.
16. London: World Scientific, pp. 229-247. 8 Prusinkiewicz, P., and A. Lindenmayer. 1990. The Algorithmic Beauty of Plants. New York: Springer-Verlag.
9 Prusinkiewicz, P., A. Lindenmayer and F. D. Fraccia. 1990. Synthesis of space-filling curves on the square grid. In Fractals in the Fundamental and Applied Sciences, eds. H.-O. Peitgen, J. M. Henriques and L. F. Penedo. Amsterdam: North-Holland Press, pp. 341-366.
10 Rosenfeld, A., and R. Siromoney. 1993. Picture languages?a survey. Language of Design 1:229-245.
11 Siromoney, G. 1978. South Indian kolam patterns. Kalakshetra Quarterly 1:9-15.
12 Siromoney, G., and R. Siromoney. 1987. Rosenfeld's cycle grammars and kolam. In Graph-Grammars and their Application to Computer Science, Third International Workshop 1986, ed. . Ehrig, M. Nagl, A.Rosenfeld and G. Rozenberg. Lecture Notes in Computer Science, no. 291. Berlin: Springer-Verlag, pp. 565-579.
13 Siromoney, G., R. Siromoney and K. Krithivasan. 1974. Array grammars and kolam. Computer Graphics and Image Processing 3:63-82.
14 Siromoney, R. 1986. Array languages and Lindenmayer systems. In The Book ofL, eds. G. Rozenberg and A. Saomaa. Heidelberg: Springer-Verlag, pp. 413^26.
15 Steinmann, R. M. 1989. Kolam: Form, technique, and application of a changing ritual folk art of Tamil Nadu. In Shastric Traditions in Indian Arts, ed. A. L. Dallapiccola. Stuttgart: Steiner, vol. 1, pp. 475^9
16 Marcia Ascher, The Kolam Tradition.
青山不改,綠水長流,在下告退。
轉發隨意,轉載請聯絡張大少本尊。