- 「拓撲學」起初叫形勢分析學,這是由德國數學家萊布尼茨1679年提出的。Topology這個英文詞是由德國數學家、物理學家J.B利斯廷1847年提出的,源自希臘文τδποζ(位置)和λδγοζ(研究),直譯是“地誌學”,最早指研究地形、地貌相類似的有關學科。我國在1956年統一的《數學名詞》中,才把它確定叫作“拓撲學”,是按音譯過來的。拓撲學是研究幾何圖形或空間在連續改變形狀後還能保持不變的一些性質的學科,即:只考慮物體間的位置關係而不考慮它們的形狀和大小。重要的拓撲性質包括緊緻性和連通性。形式上講,拓撲學主要研究“拓撲空間”在“連續變換”下保持不變的性質。可通俗地理解為“橡皮泥幾何學”。在自然現象與社會現象中,普遍存在著連續性與離散性這對矛盾。同樣,數學學科也可粗略地分為連續性數學與離散性數學兩大門類。拓撲數學對於連續性數學自然起到了帶有根本意義上的提升,而對於離散性數學也起到了巨大的推進作用。拓撲學的重要性,體現在它與其他數學分支、其他學科的相互作用。拓撲學在泛函分析、實分析、群論、微分幾何、微分方程等其他許多數學分支中都有著廣泛的應用。拓撲學與微分幾何學有著血緣關係,它們在不同層次上研究流形的性質。
- 「拓撲學」運用到工程設計上,表現為連續拓撲最佳化技術的開發利用。所謂連續拓撲最佳化是指在滿足一定約束條件下,尋求結構材料空間分佈形式,以實現置頂目標的最最佳化。Joshua Mathew等人利用該技術建立了一定體積比約束下最大化結構剛度最佳化模型,試驗結果發現:在純剪力作用下,單個框架內交叉斜杆的最大水平抗力支撐形式為45°交叉設定;而在一般的側向彎剪荷載作用下,交叉斜杆的最大水平抗力交叉點在3/4的高度位置,即距頂部1/4高度的位置。附例:中信金融中心大廈,位於廣東省深圳市的深圳灣,由一幢311.4M高和一幢211.4M高的雙塔樓和裙房組成,美國SOM公司設計。該樓抵抗水平荷載(風、地震)的結構是外圍鋼管砼斜交網格和內部核心筒剪力牆,其斜交網格的交點就是按照距頂1/4網格設定的。鋼管砼橫截面從首層500MM×500MM漸變至1700MM×1700MM,全高設定,使用420MP高強度鋼材製成。
- 拓撲最佳化技術的運用,揭開了工程上交叉支撐最大水平抗力的交叉點位置的秘密,打破了人們的傳統認知——交叉支撐總是順著對角線設定,自然交叉點在1/2高位置,從來沒想過別的形式。如果說在科學界存在著1/4最佳結點的話,那麼在自然和社會界是否也存在1/4最佳結點呢?細細想來,還真是有不少與4或1/4有關的結點。1)從伏羲“一畫開天”說起,太極生兩儀,兩儀生四象——少陽、老陽、少陰和老陰。以一天來說,從早晨開始,由少陽轉向老陽;正午以後,老陽慢慢轉向少陰;黃昏到半夜,少陰再變成老陰。以一年來說,一年有四季,春天(少陽)、夏天(老陽)、秋天(少陰)和冬天(老陰)。2)在日常工作中(以建築公司為例),對於專案,通常每週(1/4月結點)召開一次監理例會,一個月有四個星期,共召開四次例會,月底作小結;對於公司,通常召開季度(1/4年結點)經濟分析會,半年作中期總結,查詢不足並分析原因,及時提出預警;年底作全年總結和佈置來年工作計劃。這些1/4時間結點,符合天時、國情和人們的心理期望,從目前看是最佳的時間結點安排。
- 從內在力支撐的科學證明和外在的實踐表現看,都有力地說明了1/4結點(時間的或其它的)是一個很有趣的最佳結點,因為是有理數,不免少了些神秘。但無論如何,我們不防多關注一下1/4這個有趣的結點,比如:1)每天下班前1/4時段內作部門日總結和部置明天的任務;2)為防風險,拿出自己存款的1/4用於炒股,等等。
- 連續拓撲最佳化技術不但可以用來最佳化結構設計,還可以用來最佳化建築設計、規劃設計及裝飾設計等等,尤其是在概念設計階段。
sponsored links
瞭解「拓撲學」與有趣的[1/4]結點
分類: 家居
時間: 2021-12-17
相關文章

280m²大平層,簡單純淨的輕奢美宅
案例名稱:美的廣場 案例房型:大平層 設計風格:現代輕奢 案例地址:佛山順德 本案處於中心地帶,景觀層次豐富,視野開闊,環境清幽,推開窗就能看見風景,回到屋內就能享受簡約優雅.溫暖舒適的居住環境. 客 ...

150平米輕奢五室大戶型,有三個明衛,主臥配置空中半島觀景衛浴
如果沒有辦法南北通透,那這個戶型還有辦法讓人滿意嗎?答案是肯定的!這個150平米的戶型,就讓您感受到精緻的輕奢和極致實用性的完美結合.讓我們詳細來看一下. 子母門入戶,門口是一個非常寬敞的書房,有獨立 ...

207平米輕奢氣質大平層,陽臺長度高達14m,客廳開間近7.6m
207平米的大戶型,可以擁有怎樣的奢華感受?今天讓我們就來體驗一下這個特立獨行的大平層. 電梯獨立門廳,透過子母門入戶,有一個單獨的玄關,可以做一排衣帽架,也可以放一個玄關櫃.作為潔汙分割槽的過渡轉換 ...
好房不怕等!這169㎡裝一年,頂樓大平層的輕奢,藏不住的高階感
俗話說得好,"佛靠金裝,人靠衣裝",而家得靠心去裝~ 這家的屋主很隨心了,不做到自己很喜歡的絕不會放進自己家裡,斷斷續續地花了一年多的時間才把家裡佈置成他們心裡的樣子,頂樓的169 ...

當輕奢遇上美式,一場視覺美學正在上演
風格對於室內設計來說就是整個內部空間的核心,好的風格會成就很好的視覺觀感.單單風格這塊,我們也曾聊過很多,北歐.現代.新中式.日式.美式.工業風.混搭......每一種風格的呈現,都會給一個原本寡淡的 ...

256㎡現代輕奢,精緻、簡約的設計往往更加的適合生活,這就是家
過度奢華總會讓人產生距離感,而精緻.簡約的設計往往更加的適合生活.也正是因為如此,所以近幾年才開始非常的流行輕奢風格的裝修,因為它的特點剛好符合這眾多的要求,符合人們對家的審美觀. 本案介紹的是一套大 ...
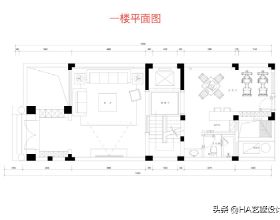
500㎡歐式與輕奢混搭,打造金碧輝煌的豪宅
今天要介紹的案例設計業主是一對中年夫妻,自己創業,性格十分爽朗.一開始夫妻倆為了出行方便,本來是打算在市中心購置一套大平層,可在去過一次朋友家後,一下子就被朋友前有花園,後有庭院的獨棟別墅吸引,於是, ...

迪麗熱巴運動裝扮可鹽可甜,穿牛油果綠竟沒翻車,私服審美也超絕
#今天穿什麼##潮流風格穿搭##時尚# 舒適感不僅僅是身體對服裝的需求,很多時候也成為了一種時尚穿搭的氛圍感,那種慵懶的整體氛圍,那種充滿著向上的生命力色彩,絕對的不受約束,為身體和動力而服務. 而將 ...

寶芸邸家居丨輕奢系列:莫奈花園
莫奈花園位於法國巴黎以西70公里的吉維尼小鎮上,是法國著名畫家莫奈的故居.莫奈在這裡完成了他的著名作品<睡蓮>系列和<日本橋>系列. 世界自然風光設計系列:最美不過天生之美! ...

閨蜜的130平米新家,裝現代輕奢風格,單一個沙發牆就把我迷住了
家,是有人才會有人氣,如果單身一人或者兩夫妻居住,再大的房子心中都會有一些空蕩感,一家三代人同居在一起,家庭氛圍也是非常的溫馨幸福.無論裝修什麼風格,只要一家人在一起便能夠映襯出屋內幸福的氛圍. 本案 ...

139㎡美式輕奢新房,高階灰+金屬感,還有高顏值衣帽間強勢入鏡
本案例是一套面積139㎡的新房,四室兩廳兩衛的戶型,整體以美式輕奢風格為主,加上高階灰+金屬感的搭配,使整個家看上去倍有格調感.下面就和齊家云云一起來看看吧,希望大家喜歡~ ▲入戶玄關,一進門精緻鞋櫃 ...
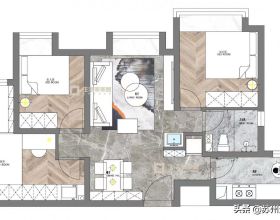
95平米 輕奢風格
95㎡戶型不算很大,但只要在裝修計劃上多用心,小空間也可以實現大視野.這個案例是以一種簡約輕奢的風格設計的.淺灰色系和簡約輕奢風格傢俱燈飾使整個空間更加和諧,想必屋主住在裡面十分愜意. 整體平面佈局 ...
114㎡現代質感輕奢風,新家裝修就這麼設計
■ 案例簡介 □ 建築面積 | 114.54㎡ □ 房屋戶型 | 3室2廳2衛1廚 □ 裝修風格 | 輕奢風 □ 座標 | 江西撫州東鄉 平面戶型圖 △△△ "1 輕奢風 輕奢,是用低調的方 ...

125㎡“雙橡園”輕奢現代風
案例引言 「採光」是許多人在買房時重要的考量之一,充沛的光線引入,不論室內坪數大小或格局是否方正,都能有效提供人們更寬廣舒適的視覺感受! 但並非所有房子都能十全十美. 來自雙橡園R1特區的林屋主,因為 ...

陽光城翡麗灣580m²現代輕奢風別墅,演繹簡潔低調美宅
玄關 地點丨泉州陽光城翡麗灣 風格丨現代輕奢風 面積丨580㎡ 造價丨 60萬 一樓客廳 一樓背景牆 5米高的電視背景牆,全大理石鋪貼,紋理縱橫交錯,遠觀彷彿九州星河,恢弘大氣.整排的落地窗不僅能飽覽 ...

新力琥珀園220㎡複式樓現代輕奢,巖板+護牆板,這才叫真正的高階
同樣的房子因居住人員的不同,而有著不一樣的氣息.如何打造出具有品質感的生活,這就意味著設計師必須要有更強的設計張力,像對休閒質感.高階元素.設計機能舒適度...等有著張弛有度的綜合空間把控力.透過與業 ...

玫瑰島全景櫃,精緻收納、輕奢有度
生活環境折射了不同的人生態度,有的人在無序中得過且過,生活一地雞毛,有的人擅長劃定規則,追求秩序和效率,他們的生活則是乾淨舒適的.居所不亂,窗明几淨,收納有序,不僅能保證生活品質,還能釋放現代人的焦慮 ...

無覓造園:海南42平的現代輕奢花園怎麼做呢?
造一座花園,追尋陶淵明式的閒散悠然的田園生活. 專案名稱:素錦年華-藏在花園裡的輕奢現代風 專案地址:海南 設計單位:無覓造園卓一卓設計團隊 專案面積:42m² 現代輕奢的混合式花園越來越受到大家的追 ...

300㎡現代風,活潑撞色設計,輕奢質感美不勝收
現代家裝的風格,輕奢風是大家最多的選擇.更多的年輕人選擇把自己的新家收拾得別具一格,更有特色,本案例便是採用的現代輕奢風,配有現代風格的多種元素混搭,打造一款華麗而又使用的家裝樣板. 設計師在接到客戶 ...

