“大衍之數五十,其用四十有九”出自《周易.繫辭上傳》:
大衍之數五十,其用四十有九。分而為二以象兩,掛一以象三, 揲之以四以象四時,歸奇於扐以象閏,五歲再閏,故再扐而後掛。 天一地二,天三地四,天五地六,天七地八,天九地十。天數五,地數五,五位相得而各有合。天數二十有五,地數三十,凡天地之數五十有五。此所以成變化而行鬼神也。
玄幻或修正則喜歡用“大道五十,其用四九,人遁其一”的說法。個人不喜歡太玄乎的說法,一些很玄乎的理解,比如天數地數,或者又如十天干、十二地支、二十八星宿合計五十數,就不多解釋了,這裡給大家說一種很科學很實用的理解。
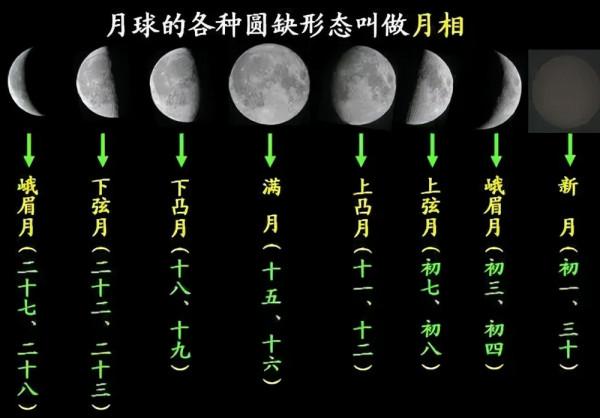
首先,大家都比較理解現在的星期制度,然而這種星期制度並不與天文關聯,而實際中國早期的星期制度是與月相直接關聯的(之後再變為七曜七政)。月相是日地月三者不同的幾何關係造成地球上看到月球的光面的不同形狀和起落時間,其週期為29.53天,月相包括以下幾種:
月相在朔月(新月)、上弦月、望月(滿月)、下弦月是最好認出的,用四種月相就可以劃分出4個“周”,每“周”為7-8天(後文為了方便,用“周”或“自然周”表示)。這可能是中國最早、世界最早的的星期制度(西方的說法是他們公元321年開始的,按照周易的時間也得公元前1000年,另有種沒查證的說法,公元前1600年的商朝,把一個月分為4周,大月中有兩週是7天,兩週是8天;小月中有三週是7天,一週是8天)。
則一年有周數為:365.25/29.53*4=49.475,即近50個自然周(大道五十),一年永恆固定的是49個周(其用四十有九),而另外一個周,有時有,有時沒有,這就是“大衍之數五十,其用四十有九”。用陰曆如此來合陽曆,則兩者相差只有3-4天(嚴格計算也是3.5天),這是49之外的餘數,而且這些誤差後文還說了用“閏”的方法來消除,有閏周的年份即出現第50個周。這種對易經“大衍之數五十,其用四十有九”的看法,也是與我國唐朝的天文學家僧一行(683年-727年)相一致的,他是在我國和世界上最早測定地球子午線(經度)1度長度,其制定的《大衍曆》也因此而得名。
另外,有專業背景的可去研究下“衍”字有無反射或者月亮的意思,據東漢張衡《靈憲》:“夫日譬猶火,月譬猶水,火則外光,水則含景。故月光生於日之所照,魄生於日之所蔽”,其中就有大意說月像水,能夠反射太陽。
說到這裡,大家可能大概看明白了,這實際是中國秦漢更早之前,把陰曆和陽曆進行合曆的另一種方法,而用到現在的農曆一年通常是354天左右或者384天左右,這樣每年差異的天數太大,而且和陽曆最大可能相差出一個月,這對於農業的影響是比較嚴重的(後來的農曆用24節氣彌補上了這個缺點),而陰曆透過月相即可知道大致日期,這是有很大優勢的,尤其對於古代交通不便,農政的政令下發不到偏僻之處的情況。
繼續看繫辭原文,看我們說得是否合理:
- “分而為二以象兩,掛一以象三”,可以這樣理解,49先分出1不管,然後對半分,即49個自然周分為三部分:24、24、1,如此就分出了上半年和下半年,分出了陰陽與寒暑,而對於分出的1周,可能只是多餘之數,也可能是用來過年(參考中國其他古代曆法,360天之外的5~6天用來過年)
- “揲(shé)之以四以象四時”,即24周再對摺,變為12、12、12、12、1,其中12個自然周(即3個自然月)大致為一個季節,以與陽曆的四季相符合。
- “歸奇於扐以象閏”,即把餘數(49之外的餘數)累計起來用“閏法”來消除,餘數大致為0.475(因為古代算的迴歸年、月相週期精度不一定和我給出的一樣,其實到春秋戰國時一年的時長和月相週期的資料精度已經超越我給出的資料了,具體百度:古六歷)
- “五歲再閏”,即5年2閏,即0.475*5=2.375(如果4年,則為1.9,不足2閏,同時不說2年1閏,說明古人計算的餘數在0.4~0.5之間,另外要求這10年間,5年2閏後的餘數要最小,這裡附一個小課題,中國古人算出的49的餘數大概是多少呢?)
- “故再扐而後掛”,即餘數再積累再閏。
再之後繫辭文字“天一地二,天三地四。。。”和前文就不是一個風格了,前面講術數,後面直接“玄學”了,感覺像漢朝及後人加上去的,就懶得去搞“玄學”了。
以上是個人和歷史中一部分人的理解,不一定非常準確。最後,天文學是我們傳統文化中非常重要的文化之根,正所謂“三代以上,人人皆知天文”,懂點天文學,可以幫助我們更好讀懂我們的文化。
附錄:中國古人算出的一年49周之外的餘數大概是多少呢?
- 提示1:10年間,5年2閏後的餘數要最小
- 提示2:一年為365~366天,一月約29.5天,這種資料精度在商朝時就已經達到或超過。
有興趣的可以自己探索一下。
想知道答案的可以繼續往下閱讀:
- 在0.4~0.5之間用0.01的步長試探滿足提示1的餘數取值範圍,數學方法也可以直接計算,結果約為0.40~0.43符合,如果餘數能夠為負數,要求餘數的絕對值最小,符合的範圍還要小,約為0.40~0.416
- 一年為365~366天,步長0.1天,一月約29.5天,步長0.01天,計算兩者的比值乘以4之後的小數部分,在以上符合餘數0.40~0.43範圍內尋找答案(古代測定一月時長精度必然高於一年時長,和其時長、參考系、觀測技術等相關,在此不展開說了)。
最後的結論是表中綠色填充部分的資料較為符合,最理想的是0.4078和0.4245,即當時可能採用的資料是一年365天,一月29.55天或29.54天(現在所測資料為29.53068天)。如果以上推測正確,則比較顯然的情況是,這套制定曆法制定的時代在四分曆之前(此時已經測出一年為365.25天),另外再結合月相週期的資料可做一定推測,至於具體什麼時間,待有心人的推定了。
注:好久沒更新,抱歉!一者事多人怠,二者部分更新到了其他平臺,不一定符合各位讀者的口味。