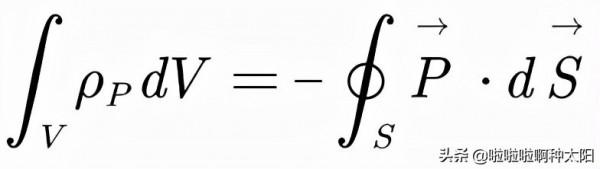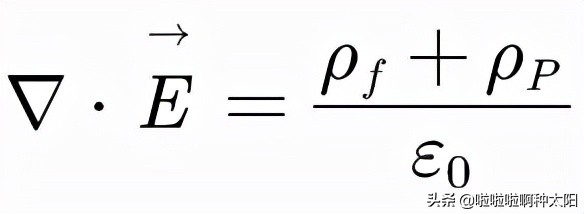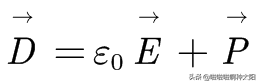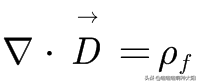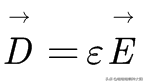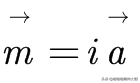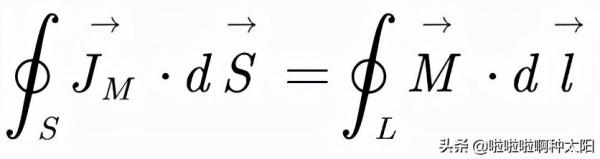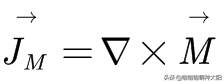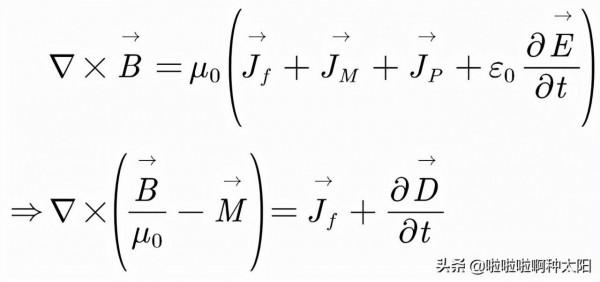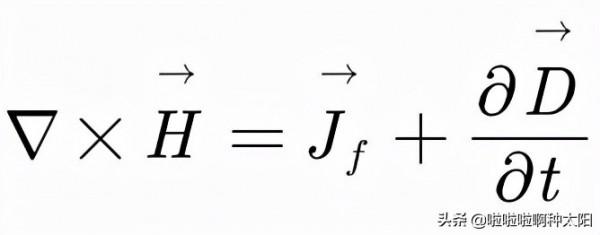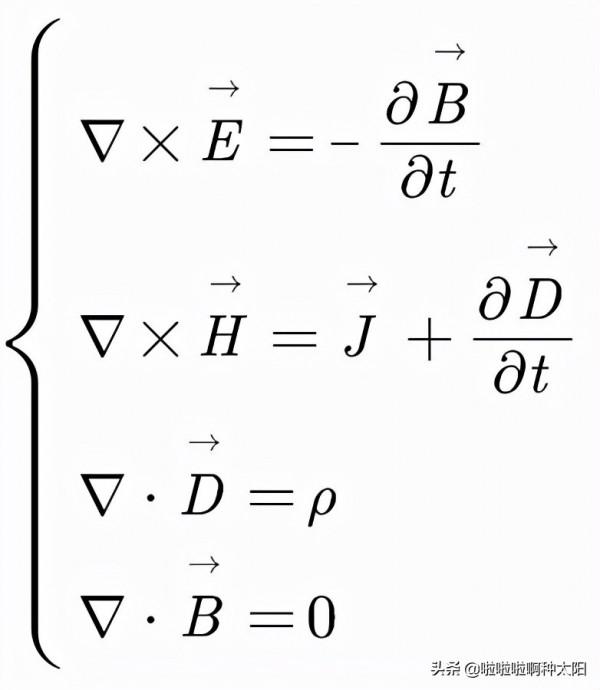神奇的電磁世界：電動力學(麥克斯韋方程組02)

如果喜歡的話請點點關注和轉發哦，謝謝大家啦！

這個月要期末考試，因此沒什麼時間更新，抱歉各位。

介質的極化

在討論介質中的麥克斯韋方程組之前，我們先要明白，電磁場的來源是電流和電荷，也就是說，只要空間中某處有電流和電荷的存在，那麼該處就會產生電磁場。

在這一認知的幫助下，我們就可以透過尋找電磁介質中電流和電荷的總體分佈來研究介質中的電磁場。

我們將一電介質放入電場中，正負電荷在外電場的作用下被拉開，形成電偶極子，這一過程就叫做極化。

電介質又存在著兩種情況：

第一種電介質是在沒有外電場的情況下，分子的正電中心和負電中心是重合的，沒有固有的電偶極矩。當被放入電場中時，所有的正負電荷均沿著電場的方向被拉開，就會出現宏觀電偶極矩的分佈；

第二種電介質在沒有外電場的情況下，分子的正電中心和負電中心並不重合，本身是存在固有的電偶極矩的，但是由於分子的排列是無規則的，所以在宏觀上並以沒有電偶極矩分佈。當施加外電場後，在電場的作用下，有極分子的取向將會趨同，就會出現宏觀電偶極矩的分佈。

宏觀電偶極矩用點極化強度向量P來描述：

其中P_i(_i的意思是i是下標)是第i個分子的電偶極矩。

由於計劃，分子的正負電中心發生相對位移，因此在ΔV內可能出現淨餘的正電或負電，即出現宏觀的束縛電荷分佈，我們現在首先要求出束縛電荷密度和電極化強度之間的關係。

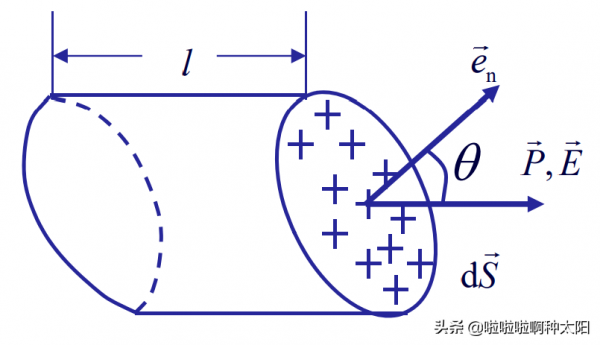
設每個分子由相距l的一對正負電荷q構成，分子的電偶極矩為p=ql，當電偶極子的負電荷處於體積l·dS內時，同一偶極子的正電荷就傳出介面dS外邊。設單位體積分子數為n，則穿出介面的正電荷為：

假如介面S為包圍閉合區域V的必和介面，那麼穿出的正電荷就是：

由於介質本身是電中性的，因此正電荷的量也等於V內淨餘的負電荷，而這種由於極化出現的電荷分佈稱為束縛電荷，用ρ_p來表示束縛電荷密度，就有：

利用高斯公式我們可以得到上式的微分形式：

在介質中，介質的極化產生束縛電荷的分佈，而束縛電荷又會激發電場，兩者相互制約。因此對於介質中的電荷密度，我們既要考慮自由電荷，也要考慮束縛電荷，根據麥克斯韋方程組，相應的，我們就有：

為了方便書寫和討論，大家就想讓這個式子能夠簡單一些，於是我們將上式透過移項得到：

這裡我們引入電位移向量D，定義為：

這樣我們就得到了一個非常簡單的關係式：

電位移向量是一個幫助我們便於討論的輔助場量，而這個輔助場量顯然只和自由電荷密度有關。

為了求解方程，我們還需要知道D和E之間的關係。對於一般各向同性線性介質，我們有：

χ_e稱為介質的極化率，ε稱為介質的電容率，ε_r為相對電容率，將P帶入電位移向量定義式：

介質的磁化

介質分子內的電子運動構成微觀分子電流，在外磁場的作用下，分子電流的取向將會變得有規則，形成宏觀磁化電流密度J_M。微觀分子中電子的運動，可以等效成載有電流i，面積向量為a的電流環。每個電流環都有磁偶極矩：

介質磁化後，出現宏觀磁偶極矩分佈，用磁化強度M來表示，它定義為ΔV內的總磁偶極矩與ΔV之比：

接下來我們需要求出磁化電流密度J_M。

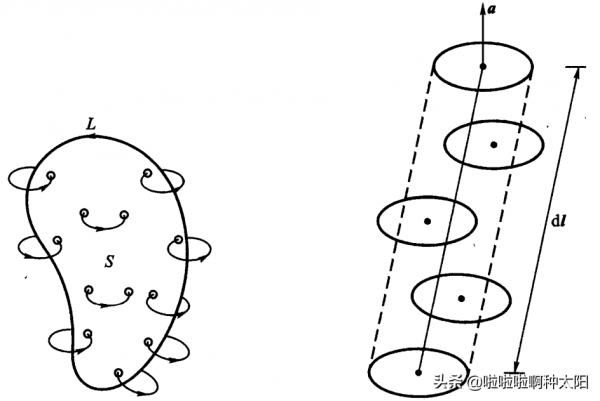
由圖可知，透過S的總磁化電流I_M等於邊界線L所

鏈環著的分子數目乘上每個分子的電流i。因為若分子電流被邊界線L鏈環著，該分子電流就對S的電流有貢獻.在其他情形下，或者分子電流根本不透過S，或者從S背面流出來後再從前面流進,所以對I_M沒貢獻。

若分子位於體積為a·dl的柱體內，則該分子電流就被dl所穿過。假設單位體積內分子數為n，則被邊界線L鏈環著的分子電流數為：

我們將分子電流數目乘以每個分子的電流i：

而根據電流和電流密度的關係，我們不難得到磁化電流和磁化電流密度的關係為：

我們將兩式相結合就可以得到：

利用斯托克斯公式，我們就能得到相應的微分形式：

當電場隨時間改變時，極化過程中正負電荷的相對位移也將隨時間改變，由此產生的電流稱為極化電流。假設ΔV內每個帶電粒子的位矢位x_i，電荷為e_i，就有：

磁化電流密度和極化電流密度之和是介質內總誘導電流密度，結合上一次我們得出的麥克斯韋方程組，就有：

這裡我們要做一個和之前類似的處理來便於討論，引入輔助場量磁場強度H：

那麼我們就有：

透過實驗，我們發現對於各向同性非鐵磁物質，M和H之間有簡單的線性關係：

χ_M稱為磁化率：

μ為磁導率，μ_0為相對磁導率。

從物理本質上看，E和B是場的基本物理量，而D和H是輔助物理量，歷史上由於人們對於磁場曾有不正確的認識，把H稱為磁場強度而和電場強度E對比，現在人們知道這種看法是錯誤的，但由於歷史原因，B和H原來的名稱仍然保留了下來。

介質中的麥克斯韋方程組

現在我們將自由電荷和自由電流的下角標f略去，將之前得到的式子與原來真空中的麥克斯韋方程組結合，得到介質中的麥克斯韋方程組：

在解決實際問題時，而我們還需要一些電磁性質的實驗關係：

在導電物質中還有歐姆定律：

下期預告

麥克斯韋方程組可以用於連續介質內部，但是在介質的分介面上，由於一般出現面電荷電流分佈，使物理量發生躍變，微分形式的麥克斯韋方程組不再適用。

因此，在下一期，我們將尋找另一種形式來描述介面兩側場強以及介面上電荷電流的關係。各位對電磁世界好奇的小夥伴，我們下期專題見啦，喜歡的話記得點一下關注哦！

編 輯|笨笨

校 對|笨笨

審 核|笨笨