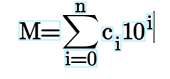老鐵們關心質數的整除性的證明、推導過程和原理，博主之前的文章裡已經描述得很詳細了。在這裡再總結一下。假設我們有一個N位數的M，可以表示為
ci為每一位數字
設A≡a Mod m，那麼由同餘定理，假設F(A)為A的整係數多項式，那麼我們可以得到F(A)≡F(a) Mod m，如下式，具體證明過程參見博主前幾篇描述：
因此，十進位制數M就相當於上式A=10的狀況，則我們可以得到如下結論：
即最後一位能整除2，5，那麼原數就能整除它
即每位數字之和能整除3，9，那麼原數就能整除它
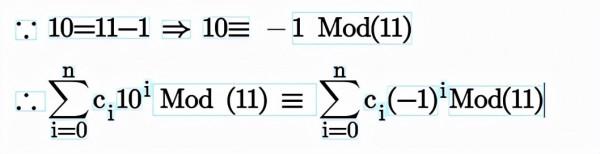
即從最右邊起，對每位順序加減，也即偶數位的數字和減去奇數位的數字和。如結果能整除11，原數就能整除它
把原數二位分割後相加，若結果能整除11，則原數就能整除它
分割後的數字，從右開始順序加減，也即偶數位的和減去奇數位的和，若結果能整除7,11,13，則原數也能整除它
分割後的數字相加，若結果能整除37，則原數也能整除它
以上是幾個對10的整數冪同餘±1的幾個質數，整除規則相對簡單。很多質數對10的整數冪同餘不是±1的怎麼判斷呢？我們就以17舉例：17*6=102，對100餘數是-2，這個就比較麻煩了，因為按照同餘定理，需要對每兩位分割的數字乘以2的對應次冪再加減，如果M有很多位，這個方法將不具有可行性。
分割後的數字要乘以2的次冪再進行加減，比以上那些數麻煩很多，如果原數有很多位，這種方法就沒有可行性。
我們的解決方案就是截尾法。假設M的尾數為b，剩下的數字為a，則M=10a+b，截尾法就是依據同餘定理，將a的係數化為1。也就是把N位數的M，轉換為N-1位的Q
下面以17為例，如果10a+b能夠被17整除，那麼5(10a+b)也可以被17整除，而5(10a+b)=50a+5b=51a-a+5b=51a-(a-5b)，51=3*17可以整除17，因此，M=10a+b與a-5b對17同餘，M是否整除17相當於a-5b是否整除17。也就是截斷M的尾數後，還要減去尾數的5倍，如果結果能被17整除，那麼原數就能被17整除。如此繼續進行，直到結果能夠容易判斷為止。
其他質數也是類似，目的就是將a的係數簡化為1，具體演算法的C#程式碼和註釋描述如下：
static int GetPrimeRuleParam(int prime)
{
switch(prime % 10)
{
case 3: return (1+prime*3)/10;//尾數為3，該數的三倍加一再除以10
//13->4，23->7，43->13，53->16，73->22，83->25
case 9: return (1+prime)/10;//尾數為9，該數加一再除以10
//19->2，29->3，59->6，79->8，89->9
case 7: return (1-prime*3)/10;//尾數為7，用一減去該數的三倍再除以10
//7->-2, 17->-5, 37->-11， 47->-14, 67->-20, 97->-29
case 1: return (1-prime)/10;//尾數為1，用一減去該數再除以10
//11->-1，31->-3，41->-4，61->-6，71->-7
default: return 0;//尾數為其他，不是質數，返回0
}
}
