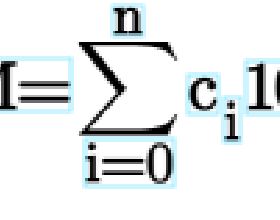1.合數只有一種質因數拆解方式。
A為合數,A可分解為a的x0次*b的ⅹ1次*c的ⅹ2次……或a的y0次*b的y1次*c的y2次……,因A若為不同的質數整除,則質數可為其他質數整除,這是不可能的,不符合質數定義。只能是質數的次數不同,若第一種拆分中,某質數p的次冪為m,另一種拆分中,p的次冪為n,m>n,A/p的n次的兩種拆分中,一種有p的m-n次,一種沒有p,這是不可能的。假設不成立。
2.兩正數小於某質數,兩正數乘積不能整除這個質數。
設a、b為兩正數,c為質數,a<c,b<c。若ab/c=k→ab=kc→c為ab的質因數,而a<c,b<c,則a的質因數<c,b的質因數<c→ab的質因數<c→矛盾→假設不成立。
3.a、b不能被質數p整除,ab不能被p整除。a/p≠整數,p不是a的質因數,同理不是b的質因數。→p不是ab的質因數→ab/p≠整數。→a、b、c、d……不能被質數p整除,abcd……/p≠整數。
4.A被B整除,B的質因數A都有,且次數不超過A中的次數。
5.最大公約數,每個共同質因數在A、B、C……中最小次冪乘積。
6.最小公倍數,A、B、C……中所有質因數最高次冪的乘積。
7.a、b、c……都與K互質,其乘積與k互質。
8.a、b、c……互質且能整除k,→a、b、c……為k的質因數→abc……能整除k
9.m、n對模a、b、c……(互質)同餘→a、b、c……整除m-n→abc……整除m-n
10.數A=a的x次冪*b的y次冪*c的m次冪……(a、b、c……為不同質數),A=k的n次冪,→K的質因數也為a、b、c……→k=a的j次冪*b的p次冪*c的q次冪……→k的n次=a的nj次*b的np次*c的nq次……→nj=ⅹ,np=y,nq=m……→j=ⅹ/n,p=y/n,q=m/n……→A的每個質因數次冪可被n整除。
11.a、b、c……互質,且等於k的n次,a可寫為l的α次*m的β次*p的γ次……(l、m、p……為質數)→a的1/n=l的α/n次*m的β/n次*p的γ/n次……→對b、c……同樣適用。
12.a、b能被k整除,且關於模m同餘→a/k=n1,b/k=n2,(a-b)/m=n3→(a-b)/k=n1-n2=n4→k與m都整除a-b,且k與m互質→(a-b)被km整除。若k、m有最大公約數e→(a-b)/km=(a/K-b/k)/m,分子分母同乘以1/e結果不變→(a/ke-b/ke)/(m/e)=(a-b)/km=整數。
13.若k與m互質,e與f關於模m同餘→(e-f)/m=n→k(e-f)/m=kn→ke與kf關於模m同餘(12的另一種表述)。
若a和m互質,e與f關於模m非同餘→a不能被m整除,e-f不能被m整除→ae與af關於模m非同餘。(12的逆定理)。→a與0到m-1中每個數相乘,並把乘積化簡為相對模m的最小剩餘,且各不相同,不超m。
14.m與a互質,ax+b與c關於m同餘→(aⅹ+b-c)/m=k→(aⅹ-(c-b))/m=k→aⅹ與c-b關於模m同餘,c-b關於模m的最小正剩餘為e→(根據上條定理)有ⅹ<m,使得aⅹ≡e(modm),令ⅹ=v,→av≡e≡c-b(modm)→av+b≡c(modm)。