已知∠A=25°，∠CBD=35°，求紅色角度數

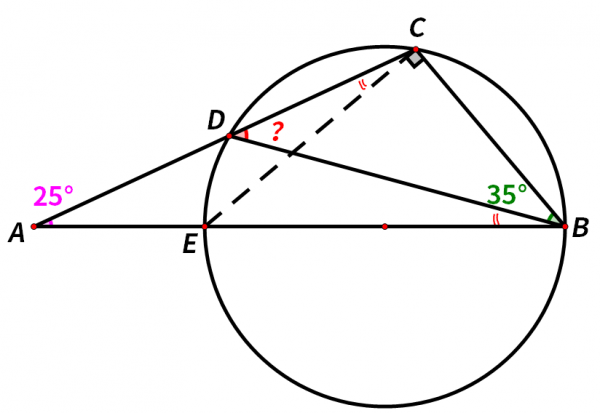
如圖，已知∠A=25°，∠CBD=35°，求∠BDC的度數。這題怎麼做呢？

根據三角形的外角定理（三角形的一個外角等於與它不相鄰的兩個內角的和），

∠BDC=∠A+∠ABD=25°+∠ABD，

也就是說要求出∠ABD的度數，就能得到∠BDC。

如何去求∠ABD呢？

圖中有圓，我們回想一下和圓有關的性質及定理。

比較常用的有同弧所對的圓周角相等，同弧所對的圓心角是圓周角的2倍，直徑所對的圓周角為90°等。

這道題我們需要用到同弧所對的圓周角相等，直徑所對的圓周角為90°。

如圖，連線CE。根據同弧所對的圓周角相等，可得∠ABD=∠ECD。

而由直徑所對的圓周角為90°，可得∠BCE=90°。

接下來看到三角形BCD，

由三角形的內角和為180°，可得

∠BDC+∠DCB+∠CBD=180°

而∠BDC=25°+∠ABD，

∠DCB=∠DCE+90°=∠ABD+90°，

∠CBD=35°，

綜上，25°+∠ABD+∠ABD+90°+35°=180°，

解得∠ABD=15°，

所以∠BDC=25°+∠ABD=25°+15°=40°。

以上就是這道題的解法。除此之外，你還有其他方法嗎？歡迎在評論區留言~