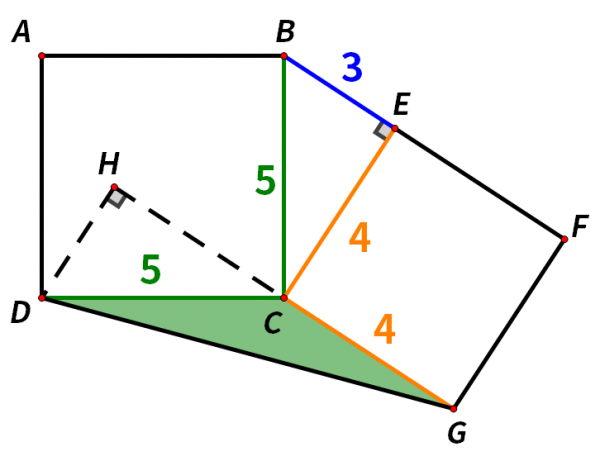
如圖，四邊形ABCD和四邊形CEFG都是正方形，∠BEC=90°，BE=3，CE=4，求三角形CDG的面積。這道題怎麼做呢？
拿圖註明來源
三角形BCE是直角三角形，BE=3,，CE=4，由勾股定理可得BC=5。
正方形ABCD的邊長為5，正方形CEFG的邊長為4，
DC=5， CG=4。
拿圖註明來源
我們已知三角形CDG兩條邊的長度，要求它的面積，接下來只要求出DC邊上的高或者CG邊上的高即可。
如圖，延長CG，過點D作CG延長線的垂線，DH⊥CH。
拿圖註明來源
接下來我們就要去求DH的長度。
我們看到三角形CDH和三角形CBE。
拿圖註明來源
在三角形CDH和三角形CBE中，
∠H=∠BEC=90°，
∠1=∠2（∠1+∠3=90°，∠2+∠3=90°，等量代換，∠1=∠2），
DC=BC，
由角角邊證全等可得三角形CDH和三角形CBE全等。
三角形CDH和三角形CBE全等， DH=BE=3。
所以三角形CDG的面積=CG×DH÷2=4×3÷2=6。
以上就是這道題的解法，除此之外你還有其他方法嗎？可以在評論區留言~
