編者按:看寒來暑往雲捲雲舒,思古往今來氣候變遷,中科院之聲與中國科學院大氣物理研究所聯合開設“大氣悟理”,為大家介紹大氣裡發生的有趣故事,介紹一些與天氣、氣候和環境相關的知識。
天氣現象大都是大氣運動的產物,氣流的上升是雨、雪出現的幕後推手,氣流的旋轉是颱風、龍捲的背景舞臺。天氣預報的精髓就是準確把握和推斷大氣運動的主要趨勢。大氣運動本身已是極具複雜性,如果再遇上覆雜的地形,摸清大氣氣流“來龍去脈”的難度又要再上一個層級。這個想想就令人頭疼的問題在數值模式中該如何解決呢?
(圖片來自網路)
充分考慮大氣物理過程——提升模式準確性的關鍵一環
地球系統數值模式的基本框架是一組描述大氣運動的物理方程組,包括空間(三維座標x、y、z)和時間(t)的變化傾向。當我們輸入某一時刻的觀測資料作為初始場,透過求解方程組就能夠計算出未來大氣的基本狀況。時空是連續的,但目前的技術不可能無縫隙地計算出地球上每一點上每時每刻的氣流情況。現有的數值模式中是透過差分計算的方法來實現模擬大氣運動的過程。時間的差分演算法表示,我們無法計算每時每刻的時間變化,但我們可以計算一定時間後的變化情況(比如30分鐘、1小時)。而空間的差分演算法在地球表面設定網格層,透過求解每個格點上的情況來反應某個區域的平均情況來實現的。
大氣運動基本方程組(天氣學原理)
數值模式對大氣的模擬能力,一方面取決於描述大氣運動的物理方程組的準確程度。在早期,這個方程組只是由幾個描述大尺度活動的相對簡單的運動規律所組成。隨著人們對大氣活動認識的逐步深入,這組方程組囊括了越來越多尺度更小的物理過程,提升了數值模式對大氣過程的再現能力。模擬能力的提升在另一方面取決於時空解析度的大小。理論上來說,時空解析度越精細,我們對大氣活動模擬的精確度越高。但時空解析度的提升,如將“每100公里1小時”的模擬提升至“每50公里30分鐘的模擬”伴隨的是計算量指數級地增加。
全球大氣模式結構示意圖(圖片來源:NOAA)
在目前的計算能力下,一般氣候模式的水平解析度通常為幾十千米,比如我國最新研發的地球系統數值模擬裝置“寰”的全球尺度水平解析度為10-25km,但一些對大氣活動有著重要影響的物理過程的空間尺度可能只有幾百米。這就意味著在現有的計算網格上無法將這些小尺度的物理過程解析出來,而忽視了它們的作用就會造成模式模擬與實際大氣運動的偏差。因此針對這些次網格物理過程,人們採用次網格過程引數化的方法將這些物理過程對大氣活動的影響反應在模式裡。引數化簡單來說就是將這些物理過程的影響量化為一定的係數,當某一區域產生了這些物理過程,區域附近的網格點需要乘以這些係數,以此來表示受到了這些物理過程的影響。
令人頭疼的地形摩擦效應
大氣活動的次網格物理過程主要位於靠近地面的邊界層裡。在邊界層裡,由於受到地面熱力動力的影響,使得大氣運動具有複雜而無規律的湍流性質。但邊界層的物理過程對於大氣活動即天氣現象的發生發展有重要作用,因此細緻而儘可能準確地反應邊界層中的物理過程是提高數值模式的準確性中的關鍵一環。而在各種邊界情況中,又數山區地形的情況最令人頭疼。暫且不論山區地形表面性質的差異,光是山脈連綿起伏形態各異這一特徵,就對氣流運動產生了極其複雜的影響。
大氣邊界層湍流結構與特徵(圖片來源:Ghanadi et al. 2017)
氣流經過複雜地形時,會受到一定程度的摩擦作用。而山地對氣流影響的複雜性體現在地形各向異性上,即同樣的地形對來自不同方向的氣流產生的摩擦影響是不同的。如果對地形效應考慮不足,就會導致數值模式的模擬結果與實際大氣情況存在偏差,從而降低模式的預報能力。最典型的例子就是地形崎嶇起伏的喜馬拉雅山區,由於難以在模式網格中反映該地區複雜多變的地形對氣流運動的影響,因而數值模式對該地區降水量模擬長期存在偏差,從而難以把握喜馬拉雅地形在極端降水和水源氣候變化中所起的作用。
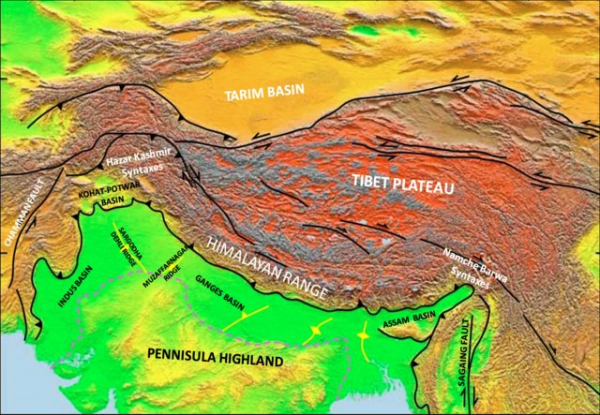
複雜的喜馬拉雅山區地形(圖片來源:Maqsood et al. 2014)
早期反映地形摩擦效應的引數化方案僅考慮了地形對於來自八個方向上(東、東北、北、西北、西、西南、南、東南)的氣流的摩擦作用。但由於相對於山地大氣中氣流是來自四面八方的,人為將氣流來向簡單劃分為八個方向的做法,會導致模式模擬的大氣的物理性質在空間上出現跳躍變化(實際大氣中各個物理量的變化是連續的)。這樣的簡化雖然在一定程度上考慮了地形的摩擦作用,但仍然與實際情況存在偏差。
早期引數化方案考慮八個方向上的氣流在經過一個網格時,受到該網格內地形阻礙程度的計算方法(圖片來源:Kim and Doyle,2005)。
近日,中國科學院大氣物理研究所LASG重點實驗室的謝瑾博博士及其合作者研發了一套能夠充分反映地形各向異性的引數化方案。實際的大氣活動是複雜的,在模式中模擬大氣活動是透過建立數理公式來實現的,因此想要在模式中儘可能地反映大氣運動的真實情況,與之相對應的數理公式往往也具有一定複雜性。透過充分考慮地形的不對稱性,地形對各個方向的氣流的有效阻礙長度,以及模式網格解析度的大小,謝瑾博博士等人研發的改進的引數化方案能夠刻畫某一地形對全方位角上的氣流的摩擦作用。
在數值模式中考察改進的地形摩擦效應的引數化方案反映不同地形的摩擦效應的能力(圖片來源:Xie et al. 2020)
對比早期的方案,改進的引數化方案提供了任意方位上的地形摩擦效應,從而保證了各個方向上氣流在運動過程中物理性質的連續性。目前這一引數化方案被應用於中科院地球系統模式(CAS-ESM)。模擬結果顯示,新的引數化方案改進了數值模式在喜馬拉雅山等複雜地形區對風速、溫度等物理變數的模擬能力。未來模式在對山區極端天氣氣候的模擬和預報能力將有所提高,從而為我國大涼山區等泥石流受災嚴重區域提供更為準確有效的災害預警。
參考文獻:
1. Xie, J., Zhang, M., Zeng Q., Xie, Z., Liu, H., Chai, Z., He, J. X., & Zhang, H. (2021). Implementation of an orographic drag scheme considering orographic anisotropy in all flow directions in the Earth System Model CAS-ESM 2.0. Journal of Advances in Modeling Earth Systems.
2. Xie, J., Zhang, M., Xie, Z., Liu, H., Chai, Z., He, J. X., & Zhang, H. (2020). An orographic drag parametrization scheme including orographic anisotropy for all flow directions. Journal of Advances in Modeling Earth Systems, 12, e2019MS001921.
3. Kim, Y.-J., & Doyle, J. D. (2005). Extension of an orographic-drag parameterization scheme to incorporate orographic anisotropy and flow blocking. Quarterly Journal of the Royal Meteorological Society, 131, 1893–1921.
4. Ghanadi, F. , Emes, M. , Yu, J. , Arjomandi, M. , & Kelso, R. . (2017). Investigation of the atmospheric boundary layer characteristics on gust factor for the calculation of wind load. SOLARPACES 2016: International Conference on Concentrating Solar Power and Chemical Energy Systems. AIP Publishing LLC.
5. Maqsood, T. , Kelly, J. , Ahmad, S. , Ahsan, N. , & Limited, D. . (2014). SPECULATIVE TECTONIC MODEL AND HYDROCARBON PLAY SYSTEM IN OUTER HIMALYIAN FOLDBELT OF KASHMIR.
6. 朱乾根. (2007). 天氣學原理和方法. 氣象出版社.
來源:中國科學院大氣物理研究所