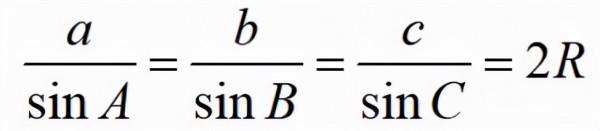三角學的起源、發展與天文學密不可分,它是天文觀察結果推算的一種方法。
在1450年以前的三角學主要是球面三角,這不但是因為航海、曆法推算以及天文觀測等人類實踐活動的需要,而且也因為宇宙的奧秘對人類的巨大吸引力,這種"量天的學問"確實太誘人了。後來,由於間接測量、測繪工作的需要而出現了平面三角。
在歐洲,最早將三角學從天文學中獨立出來的數學家是德國人雷格蒙塔努斯。
雷格蒙塔努斯,1436-1476
他在1464年完成的5卷本的著作《論各種三角形》,是歐洲第一部獨立於天文學的三角學著作,這部著作首次對三角學做出了完整、獨立的闡述,前2卷論述平面三角學,後3卷討論球面三角學。前2卷中,他採用印度人的正弦,即弧的半弦,明確使用了正弦函式,討論了一般三角的正弦定理,提出了求三角形邊長的代數解法。
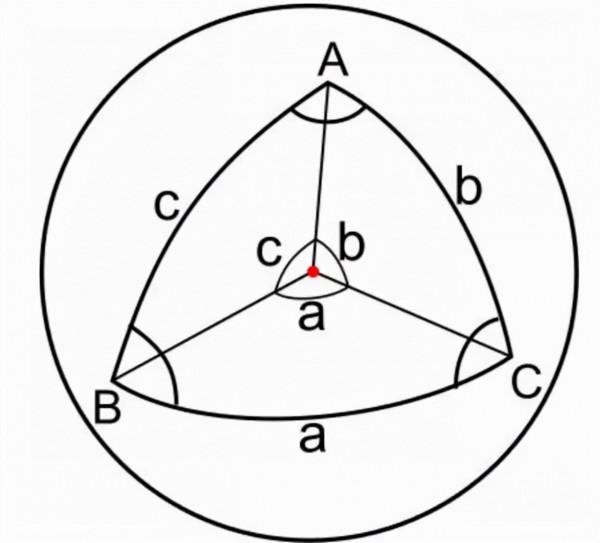
後3卷中,給出了球面三角的正弦定理和餘弦定理。他的工作為三角學在平面與球面幾何中的應用奠定了牢固基礎,對16世紀的數學家產生了極大影響,也對16世紀的數學家產生了極大影響,也對哥白尼等一批天文學家產生了很大影響。
由於雷格蒙塔努斯僅僅採用正弦函式和餘弦函式,而且函式值也限定在正數範圍內,因而不能推出應有的三角公式,導致計算的困難。後來,哥白尼的學生雷提庫斯(G.J.Rheticus,1514—1576)將傳統的弧與弦的關係改進為角的三角函式關係,把三角函式定義為直角三角形的邊長之比,從而使平面三角學從球面三角學中獨立出來。
他還採用了六個函式(正弦、餘弦、正切、餘切、正割、餘割),制定了更為精確的正弦、正切、正割表. 這些工作都極大推進了三角學的發展。實際上,由於天文學研究的需要,制定更加精確的三角函式表一直是數學家奮鬥的目標,這大大推動了三角學的發展。
韋達,1540-1603
法國數學家韋達(F.Viete,1540—1603)所做的平面三角與球面三角系統化工作,使得三角學得到進一步發展。他總結了前人的三角學研究成果,將解平面直角三角形和斜三角形的公式彙集在一起,還補充了自己發現的新公式,如正切公式、和差化積公式等。他將解斜三角形的問題轉化為解直角三角形的問題對球面直角三角形,他給出了計算的方法和一套完整的公式及其記憶法則,並將這套公式表示成了代數形式,這是非常重要的工作.
16世紀,三角學從天文學中分離出來,成為數學的一個獨立分支。微積分、物理學的研究和應用(如對振動、聲音傳播等的研究)研究和應用(如對振動、聲音傳播等的研究)中,三角學又找到了新的用武之地。