看不見的“手”——聲輻射力及其應用

|作者：臧雨宸 林偉軍 蘇 暢

(1 中國科學院聲學研究所)

(2 中國科學院大學）

本文選自《物理》2021年第11期

摘要 聲波是在彈性介質中傳播的經典機械波。當聲波在物體表面發生反射、折射、散射等效應時，會與物體產生動量與能量的交換。這種交換在宏觀上表現為聲波對物體施加力的作用，稱為聲輻射力，瑞利和朗之萬兩位科學家正是聲輻射力的最早發現者。經過一百多年的探索，聲輻射力的基本理論和研究方法已經得到極大的豐富和發展，成為聲學的前沿與熱點問題。與此同時，在生物醫學、材料科學、奈米科學等領域，基於聲輻射力的無損精準操控技術正受到越來越多的關注，展現出巨大的應用前景。

關鍵詞 聲輻射力，聲懸浮，聲操控，聲輻射力彈性成像，聲輻射力天平

1 什麼是聲輻射力

19世紀中葉，電磁學的集大成者麥克斯韋在完善電磁場理論後預言：光是一種電磁波，當光入射到物體表面時，會對物體施加壓力，稱為光壓。1901年，俄國物理學家列別捷夫首次用實驗測得了光壓的存在，有力地證明了電磁場的物質性。在此基礎上，科學家們利用光壓理論成功解釋了彗星出現彗尾的現象。和電磁波不同，聲波是在彈性介質中傳播的經典機械波，反映了由於聲源振動而引起的彈性介質週期性的膨脹與壓縮。與其他波動一樣，聲波也能攜帶動量與能量。當聲波在傳播過程中遇到障礙物時，會在物體表面產生反射、折射、散射等物理效應，並與物體發生動量與能量的交換，這種交換在宏觀上表現為聲波對物體的力的作用，稱為聲輻射力。

根據聲場的動量守恆定律可以推導得到聲輻射力的一般表示式為

其中，d = d，為物體表面的法向單位向量，為物體表面，<>稱為平均聲輻射應力張量，其具體表達式為

其中，和分別表示聲壓和質點速度，表示二階單位張量，和分別是流體的密度與縱波聲速，< >表示對物理量求時間平均。正因為聲輻射力是一個時間平均量，故而又被稱為穩態聲輻射力。

從(2)式不難看出，聲輻射力由兩部分組成。其一是聲場平方項的貢獻，對應著(2)式的第一項。線上性聲學的範圍內，聲壓在一個週期內正負值恰好完全相抵。然而我們知道，描述聲波的三個基本方程——運動方程、連續性方程和介質的本構方程都是非線性的，如果將這些非線性項考慮進來，聲壓的正負分量便不會完全抵消，在時間平均後會出現不為零的“直流”分量。圖1形象地顯示了隨著傳播距離的增加，空氣中聲壓級為140 dB、頻率為1000 Hz的聲波產生的非線性波形畸變，從上至下分別對應著馬赫數(質點振速與聲速之比)為0.002、0.003和0.004的情況。從圖中可以看出，隨著馬赫數的增加，聲波的間斷距離明顯減小，即非線性畸變更加顯著。其二是流體動量流的貢獻，對應著(2)式的第二項，這一項與聲場的非線性無關。值得一提的是，電磁場是由嚴格線性的麥克斯韋方程組描述，其輻射力僅僅源於電磁場動量流的存在，與非線性無關。從這點來看，聲輻射力的產生機理要更加複雜一些。

圖1 空氣中聲壓級為 140 dB、頻率為 1000 Hz 的聲波隨著傳播距離的增加發生了非線性畸變

聲輻射力是聲場的二階量，因而一般情況下產生的聲輻射力很小。例如對130dB(相當於火箭發射點附近的聲強)的聲波，其產生的聲輻射壓還不到0.1Pa，但當聲壓級增加到174 dB時，聲輻射壓可以達到1000 Pa。由此看來，聲輻射力主要在高聲強作用下較為顯著。

2 聲輻射力的研究脈絡與方法

早在20世紀初，聲學界的兩位集大成者瑞利和朗之萬就分別提出了聲輻射力的概念。瑞利對聲輻射力的描述可以總結為：在平面波傳播的情況下，隨流體質點一起運動的表面上受到一個不為零的平均壓力；假設該流體具有相同的平均密度但處於靜止狀態，後者也將承受一個平均壓力，前者與後者之差定義為瑞利聲輻射力。可以看出，瑞利聲輻射力是針對無限大流體介質中的一維平面行波而言的，實際狀態下，這樣的條件過於苛刻，很難得到滿足。但從線性聲學的角度出發，在一個理想剛性壁的管中，如果管子的直徑小於四分之一波長，則其中只有平面波傳播，從而為瑞利聲輻射力提供了一個可以實現的物理影象。後來，朗之萬取消了這一限制，重新定義了可以適用於有限寬波束的聲輻射力：聲場中隨流體質點一起運動的物體表面上受到的時間平均力與該物體後面未被擾動流體中的壓力之差稱為朗之萬聲輻射力。

然而不可否認的是，上述兩位科學家提出的聲輻射力理論都比較抽象，與實際的聲操控還相去甚遠。1934年，加拿大物理學家King首次利用嚴格的散射理論計算了理想流體中剛性球受到的聲輻射力，為之後的聲輻射力研究打下了重要的理論基礎。後來，日本科學家Awatani、Yoisoka、Hasegawa等人用同樣的方法研究了彈性球、彈性柱等常見模型在行波和駐波場中的聲輻射力，給出了若干富有價值的理論結果。進入20世紀90年代，隨著超聲換能器技術的不斷髮展，使用各種新型聲波進行微粒的聲操控與聲捕獲已經成為可能。於是，以高斯波束為代表的聚焦超聲下的粒子聲輻射力成為一時的研究熱點。1990年，佛蒙特大學的吳君汝教授計算得到了聚焦波束作用下球形和柱形粒子的聲輻射力，並進行了實驗驗證。21世紀以來，Marston、Mitri等人將聲輻射力的研究拓展到貝塞爾波束領域，以期充分利用貝塞爾波束的非衍射特性。其中，負向聲輻射力的發現尤為值得關注，它從理論上論證了利用單聲束製成的聲鑷子進行粒子捕獲的可能。隨後，Silva等人將聲輻射力的計算推廣到任意波束。近年來，隨著聲操控技術的不斷髮展，複雜模型和複雜邊界下的聲輻射力研究成為了新的熱點，本文作者所在團隊在此方面也有一些進展。

綜合來看，目前聲輻射力的研究方法大致可以分為散射法和數值法。其中，散射法基於嚴格的波動理論，可以得到有利於引數化分析的解析解，但當模型較為複雜時計算比較繁複，因此散射法主要用於高斯聲束、貝塞爾聲束等作用下圓柱、球等規則物體的聲輻射力計算。利用散射法可以計算得到平面行波場對剛性球的聲輻射力隨無量綱頻率的變化關係，是聲波的波數，剛性球的半徑，結果表明，剛性球的聲輻射力隨著的增加先增大而後趨於穩定。當聲場比較複雜、物體形狀不規則時，利用散射法推導聲輻射力的解析解往往是很困難的，此時可以考慮藉助純數值的方法來計算，如有限差分法、有限元方法、邊界元方法等，其中應用最廣泛的是有限差分法。該方法直接從聲波的三個基本方程出發，不需要任何形式的匯出方程，對所研究物件的形狀和尺寸沒有任何限制，但計算所消耗的資源較大。2010年，中國科學院深圳先進技術研究院蔡飛燕等人利用有限差分法計算了彈性柱的聲輻射力特性，其結果與解析解符合得很好。2015年，陝西師範大學孫秀娜等人運用該方法分析了離軸情況下剛性球的聲輻射力，結果表明剛性球在高斯聲場中的聲輻射力隨著粒子離軸距離的增大而減小。

此外，在高頻和低頻情況下，還可以分別利用聲線法和梯度法進行簡化處理。高頻條件下，物體的尺寸遠大於聲波波長，此時聲波的波動性可以忽略，只需考慮其粒子性即可。因此，我們可以利用聲線的疏密來表徵聲能量的強弱，從而用射線理論來計算此時的聲輻射力。2005年，Lee等人最早利用聲線理論研究了流體介質中任意位置粒子的聲輻射力特性，從理論上證實了聲捕獲的可能。低頻條件下，物體的尺寸遠小於聲波波長，此時物體對聲場的影響可以忽略，可以認為聲能密度在空間是連續分佈的，因而聲輻射力可以近似表示為某種勢函式的空間梯度，如同電場力可以表示為電勢能的空間梯度一樣。前蘇聯科學家Gor′kov最早計算得到了低頻情況下聲輻射力所對應的時間平均勢函式，從而大大簡化了聲輻射力的運算。

3 對抗重力的聲懸浮

從古至今，人們一直渴望能夠擺脫地面重力的束縛，像小鳥一樣在空中自由翱翔。明代的萬戶是世界上第一個想到藉助火箭推力升空並付諸實踐的人，但卻為此付出了生命的代價。近代的工業革命促進了熱氣球、飛機等飛行器的相繼問世，無疑讓人們實現了亙古的飛天夢想。然而，人們與重力的對抗才剛剛揭開序幕。1901年，英國科幻小說家赫伯特·喬治·威爾斯在《月球上最早的人類》一書中最早提出了反重力裝置的概念，他設想有一種能夠遮蔽引力的金屬叫“卡弗質”，只要把它放在飛船下面，就可以遮蔽地球引力。他製造了一艘遊艇，在下面遮蔽了地球引力，上面向月球開啟引力，遊艇就把他送上了月球。遺憾的是，迄今為止這種夢幻式的宇宙航行還沒有實現，人們還是在地球上費盡九牛二虎之力設法對抗地球引力，透過加大能源的消耗來實現“反重力”，讓自己飛向茫茫太空。

“卡弗質”的出現也許還在很遙遠的未來，但擺脫重力的懸浮技術已經變成觸手可及的現實。在航天工業和材料科學等領域，無容器環境對研究凝聚態物理是非常重要的實驗條件。目前地面上模擬空間無容器環境的方法主要有自由落體方法和懸浮方法。與自由落體方法相比，懸浮方法可以獲得持續的微重力和無容器狀態，因而應用更加廣泛。常見的懸浮方法主要有氣動懸浮、電磁懸浮和聲懸浮。氣動懸浮的懸浮力來源於氣體掠過表面時的動量減少，其穩定性較差。電磁懸浮的穩定性很好，但只適用於導電體與磁體。而聲懸浮技術對材料的物理限制較少，且較為穩定。

圖2 聲波使Kundt管中的塵埃微粒有序懸浮跳動

有趣的是，歷史上的聲懸浮完全誕生於一次意外的偶然。1866年，年僅27歲的德國物理學家Kundt在進行固體和氣體的聲速測量實驗時意外發現：諧振管中的聲波能夠讓塵埃顆粒有序地懸浮和舞動，這些灰塵微粒有序的懸浮跳動正是聲懸浮。圖2是Kundt當時所用諧振管的示意圖，管內兩列振幅相同、傳播方向相反的行波疊加形成駐波場，波節處聲壓為零，微粒始終保持靜止，其餘位置處的微粒將來回跳動，其中波腹處的聲壓最強，微粒跳動最劇烈。Kundt也因此成為發現聲懸浮現象的第一人，但當時人們並不十分清楚這一現象的產生機理。直到1934年King給出理想流體中剛性球聲輻射力的計算結果，揭示了聲懸浮來源於高聲強作用下的非線性現象。1964年，美國明尼蘇達州立大學的Hanson等人基於King的理論製造了第一臺用於研究單個液滴動力學行為的聲懸浮器。1975年，美國科學家Whymark利用聲懸浮實驗研究了鋁、玻璃等聚合物在無容器條件下的熔化和凝固過程。1992年，科學家在太空梭上利用超聲駐波場產生輻射壓力使材料浮起不接觸容器壁溶解，合成了用於製造非可視域低損耗光纖的高純度玻璃材料。經歷了一個多世紀的發展，聲懸浮從一項偶然的發現逐漸發展成為了一種成熟的技術手段，為各種材料的無容器處理和液滴動力學等領域的研究開拓了廣闊的新天地。

圖3 小球穩定懸浮在駐波場的波節下方

聲懸浮技術中最關鍵的兩點是懸浮位置和懸浮能力，我們以最簡單也是最常見的單軸式聲懸浮系統為例作一簡單說明。在穩定的一維駐波場中，聲壓的波節位置對應著時間平均勢函式的極小值點，也是聲輻射力取零值的位置。當不考慮微小粒子的重力時，粒子將穩定懸浮於駐波場的波節處。在考慮粒子重力的情況下，必須藉助一定的聲輻射力來克服自身的重力，此時的穩定平衡位置將會稍稍偏離駐波場的波節，如圖3所示。有必要指出，聲輻射力是一個瞬時變化的物理量，這裡的聲輻射力取零是時間平均的效果。由於聲波一個週期的時長很短，我們肉眼根本觀察不到小球瞬時的快速振動，而只能看到其運動的平均效應，從而認為其在聲場中保持穩定的平衡。懸浮能力主要體現為該系統可以懸浮物體的最大密度。為了提升懸浮能力，往往需要增加發射換能器的聲壓振幅，並對發射端和反射端進行相應的最佳化設計。此外，當諧振模式較低，聲壓波節較少時，懸浮能力也會得到一定的增強。2002年，西北工業大學解文軍等人成功實現了對地面上密度最大的固體銥和密度最大的液體汞的穩定聲懸浮(圖4)，從而證明了原則上可以對地面上的任意物質進行聲懸浮。該課題組還利用聲懸浮裝置進行了液滴物性引數的非接觸反演測量研究，包括密度、粘性係數、表面張力和比熱等，並對懸浮液滴的動力學行為進行了理論計算與實驗觀測。

圖4 地面上密度最大的固體銥(a)和密度最大的液體汞(b)的聲懸浮

4 聲鑷子和聲馬達

4.1 聲鑷子

日常生活中，我們經常會用鑷子來抓取那些肉眼可見但用手卻抓不住的小物體，但對於細胞、分子等微小粒子的操控，普通的鑷子就無能為力了。20世紀70年代，美國科學家阿什金(A. Ashkin)最早提出可以利用光的輻射壓力對微小物體施加力的作用。1986年，他成功將這一設想變成了現實，製成了世界上第一臺用鐳射來實現粒子操控的裝置，稱為光鑷子。現如今，光鑷子已經被廣泛運用到病毒、細菌、細胞等微粒的無創操控中，大大促進了生物技術的發展，阿什金教授也因此榮獲2018年諾貝爾物理學獎。

儘管如此，光鑷子仍然具有自身的侷限性。首先，光鑷子對樣本的透明性要求很高；其次，聚焦鐳射的高能量往往會引起粒子的區域性升溫從而造成對樣品的損傷。在阿什金製成光鑷子僅僅5年後，吳君汝教授便成功進行了聲鑷子的設想與實驗，他採用兩個平行對立放置的3.5 MHz聚焦超聲換能器形成駐波場，實現了對直徑為270μm的乳膠粒子和蛙卵的捕獲和操控，首次證實了聲鑷子的可行性。誠然，聲波的能量遠不能與鐳射相比擬，但聲波可以在固體、流體等任意介質中傳播，不受介質電磁特性和透明性的影響。另一方面，其能量與工作頻率和醫學超聲成像系統的引數相當，可以實現對單個細胞或顆粒的操控，並確保生物組織和目標粒子有足夠的安全性。

圖5 利用聲表面波實現對微粒的排列和操控，其中(a)，(b)是放置在晶片上的聲鑷系統，(c)，(d)和(e)，(f)分別是駐波場作用下對微粒的一維和二維操控

駐波場具有較強的空間能量梯度，因而更容易產生明顯的聲輻射力來實現對特定微粒的捕獲。當微粒落入這樣的聲場中，其在聲輻射力的作用下將被推到並鎖定在時間平均勢函式的極小值位置，如同被鑷子牢牢夾住一樣。在此基礎上，透過調節聲場改變波腹和波節的分佈，從而將微粒移動到理想的位置。從操控的維度來看，聲鑷子既可以實現一維和二維粒子的空間排列，也可以實現粒子在三維空間的移動變換。此外，由於聲波波長的尺度跨度很大，原則上聲鑷子可以操控從奈米到釐米尺寸的所有微粒，甚至還可以操控流體介質，形成特定的流場環境。2009年，美國賓州州立大學的Shi等人基於聲表面波的原理，利用兩個相對放置的叉指換能器產生駐波聲場，實現了對微小粒子的一維和二維排列與操控，如圖5所示。隨後，該團隊又利用叉指換能器和單層微流控通道實現了晶片上液滴的分類和排序，在晶片上實現了液滴微流控技術。

圖6 利用高頻超聲實現對細胞的捕獲。在換能器激發聲場之前，細胞位於距離勢阱中心 50 μm 處(a)，當激發聲場後，細胞受到輻射力的牽引作用向勢阱中心移動(b)，(c)，最終在勢阱中心處再次保持靜止(d)

駐波聲場至少需要一組換能器，或一個換能器與一個反射面，在實際的聲操控中這樣的條件往往很難得到滿足。與駐波場聲操控相比，單波束聲鑷子的裝置更加簡單，受到了研究人員的廣泛青睞。2009年，南加州大學的Lee等人用正弦訊號驅動中心頻率為30 MHz的鈮酸鋰壓電換能器來捕獲軸線上的微粒，發現當水中的球形粒子偏離軸線時，聲輻射力會將其拉回到軸線上。這一回復力現象為單波束聲鑷子提供了理論依據。隨後，他們在聲線理論的基礎上，使用30 MHz的高頻聚焦超聲成功捕獲了直徑為126 μm的油酸微粒，又利用100 MHz的高頻超聲成功實現了對細胞量級粒子的聲捕獲，如圖6所示。2016年，Ma等人基於微粒在行波場中的共振特性，在聲表面波微流控腔體內實現了對粒子的精確篩選。2017年，Chen等人透過改變激勵頻率製成“變尺度”聲鑷子，從而可以操控不同尺度大小的微粒。2018年，Zhao等人在PZT圓片上利用不同扇區的聲波干涉效應產生近似的貝塞爾聲束，透過其負向聲輻射力形成的勢阱捕獲了亞毫米尺度的微粒。同年，英國布里斯托爾大學Drinkwater教授和西班牙納瓦拉公共大學Marzo博士在美國國家科學院院刊(PNAS)上首次展示了多粒子的獨立懸浮與操控，該裝置被稱為全息聲鑷子(HAT)。HAT包含一個由256個直徑均為1cm的揚聲器組成的陣列，陣列單元之間有約23 cm的間隔，並且工作在40 kHz的超聲頻段。透過調節聲波的物理特徵，成功實現了二維和三維空間的聲波牽引技術，使25顆直徑在1—3 mm的聚苯乙烯泡沫塑膠小球執行了一系列令人驚歎的空中動作(圖7)。Marzo博士在接受西班牙科學新聞週刊的採訪時稱，他希望未來能透過全息聲鑷子在微觀尺度上操縱3D細胞並搭建出二維培養皿中無法存在的立體生物學結構。倘若這一設想變為現實，無疑將成為結構生物學領域的又一次偉大革命。

圖7 利用全息聲鑷子實現三維空間的聲波牽引

總體來看，與技術相對成熟的光鑷子相比，目前的聲鑷子在靈敏度方面還存在一定的劣勢，但我們有理由相信，隨著科學家們從原理、裝置和應用等方面對聲鑷子技術進行改良與拓展，聲鑷子必將朝著更高精度、更成熟、實用性更強的方向發展。

4.2 聲馬達

聲波不僅可以攜帶動量，還可以攜帶角動量，我們將攜帶角動量的聲場稱為渦旋聲場。渦旋聲場在傳播過程中會產生波陣面繞軸的扭轉，從而使其傳播相位關於聲束中心呈現螺旋變化的關係。定義拓撲荷數或聲場階數為一個波長的傳播距離內波陣面發生扭轉的次數，圖8顯示了拓撲荷數取不同值時聲場的波陣面形態圖。顯然，當=0時，渦旋聲場將退化為普通的平面波場。此外，拓撲荷數的正負表示波陣面的扭轉方向。當拓撲荷數非零時，我們稱聲場攜帶軌道角動量(OAM)資訊。與電磁波不同，流體中的聲波是不存在偏振現象的，因而不存在自旋角動量(SAM)，其軌道角動量就是最終的總角動量。

圖8 拓撲荷數取不同值時聲場的波陣面形態

當聲波與物體之間發生動量的傳遞時，宏觀上表現為聲輻射力的作用。我們自然地想到，聲波能否與物體發生角動量的傳遞，從而表現為力矩的作用？答案是肯定的，這種力矩稱為聲輻射力矩或聲輻射轉矩，最早由美國學者Maidanik於1958年提出。與聲輻射力有所不同，聲輻射力矩的產生必須具備兩個條件：其一，聲場是渦旋聲場；其二，物體能夠產生一定的聲吸收。華盛頓州立大學的張黎坤教授和Marston教授系統總結了聲輻射力矩的理論框架，並從理論上證明了對在軸對稱目標而言，聲輻射力矩正比於聲吸收功率、聲場的拓撲荷數，反比於聲波的角頻率。2012年，鄧迪大學的Demore等人利用1000個陣元的換能器陣列產生不同階的貝塞爾渦旋聲場來操控水中的吸聲圓片，首次從實驗上驗證了聲輻射力矩和聲吸收功率的正比關係。同年，Silva和Mitri等人成功推匯出了任意渦旋聲束對在軸球形粒子聲輻射力矩的表示式，並以貝塞爾波這一最常見的渦旋聲束為例進行了模擬。近年來，張黎坤教授課題組又詳細分析了貝塞爾聲束對離軸物體的聲輻射力矩特性和力矩反轉的機理。本文作者所在團隊首次在三維聲輻射力矩的問題中引入阻抗邊界，分析了渦旋聲場對邊界附近粘彈性球殼的力矩。

圖9 在銅板上刻蝕的阿基米德螺旋線，用其實現了聲渦旋

利用聲輻射力來操控微粒運動的技術稱為聲鑷子，利用聲輻射力矩來驅動微粒轉動的技術則被形象地稱為聲馬達。聲馬達的出現擴充了現實中聲操控的自由度，大大豐富了微粒運動的型別與方式。聲馬達技術的關鍵是渦旋聲場的產生，目前來看主要有三種方式。第一種方法是透過表面螺旋結構的聲源實現聲渦旋。2016年，武漢大學劉正猷教授課題組在銅板上刻蝕了阿基米德螺旋線，成功獲得了貝塞爾渦旋聲場(圖9)，並驅動水中的聚苯乙烯顆粒呈環狀分佈。2020年，該課題組基於同樣的原理利用矽基片製作聲渦旋透鏡，成功操控了蝦卵在聲場中的轉動，其觀測到的動力學特性與理論符合得很好。該方法具有技術簡單和成本低的優勢，但存在難以調節聲場引數的困難，且在低頻情況下龐大的結構尺寸限制了其在實際中的應用。第二種方法是透過有源相控陣技術實現聲渦旋。2016年，西北工業大學洪振宇課題組利用64陣元換能器產生二維貝塞爾渦旋聲場實現了對聚苯乙烯顆粒和水組成的兩相混合物的操控(圖10)。當顆粒尺寸較小時，會隨流體一起旋轉從而實現聲渦旋的視覺化。相控陣技術可以靈活地調節聲場和改變引數，但對每個換能器的電路均需要獨立控制，成本較為昂貴。第三種方法是透過聲人工結構和超材料實現聲渦旋。2016年，南京大學程建春教授課題組利用聲學共振原理，透過在厚度和半徑都遠小於聲波波長的平面狀共振超表面中有效地調控由聲學雜化共振所引起的等效聲波數分佈，將入射的平面聲波轉換為攜帶軌道角動量的渦旋聲場(圖11)。該方法基於聲學超構材料的特殊聲學特性和亞波長尺度的幾何優勢，有利於產生更穩定、寬頻帶且可靈活調控的渦旋聲場。

圖10 利用64陣元換能器陣列產生貝塞爾渦旋聲場，實現了微流控的精確操控

圖11 利用聲學共振結構產生聲渦旋

基於聲渦旋的聲馬達技術開闢了新的操控自由度，因而已經逐漸成為聲操控領域的熱點問題。順便指出，聲渦旋除了具備在聲操控、聲懸浮等領域向物體傳遞角動量的力學特性外，在聲學通訊領域也具有巨大的應用潛力。攜帶不同OAM的渦旋聲場之間彼此正交，恰好對應著不會發生混疊的不同通道。倘若OAM能夠與傳統的多路複用傳輸系統相容，則有望實現水下通訊技術領域的巨大變革。

5 聲輻射力彈性成像

人們很早就發現了生物組織的彈性資訊與其病理狀況緊密相關。漢代醫聖張仲景的《傷寒雜病論》中就對胸腹部的按診進行了詳細的論述，現已成為診斷和治療疾病的重要依據。儘管如此，單純依靠手指的觸控去定性地感知組織的彈性無疑對醫生的經驗有較高的依賴，甚至不同的醫生會得出截然不同的診斷結果。此外，對於體內較深部位的器官，人工按診也無法準確獲知其彈性和硬度的資訊。為了彌補傳統按診法的缺陷，人們致力於發展多種對組織的成像方法，希望能夠精確有效地反演出組織的彈性資訊，在這一需求背景下，超聲彈性成像方法應運而生。

根據激勵源的不同，我們可以將目前在臨床上廣泛使用的超聲彈性成像方法分為兩大類。第一種是準靜態壓縮彈性成像，最早由美國教授Ophir和日本學者Yamakoshi於20世紀90年代提出。該方法透過在組織外表面施加一定的壓力使人體組織發生形變，再利用B超波束對其進行掃描監測產生組織的應變圖。這種方法的侷限性在於它仍然只能探測到淺表的組織資訊並且容易受到邊界條件的影響。此外，它無法給出組織硬度的具體數值，只能反映和背景組織相對比的一個相對大小。第二種是基於聲輻射力的動態彈性成像技術，該技術使用超聲波對組織施壓，很好地克服了傳統準靜態壓縮彈性成像中無法對深部組織成像的問題以及易受邊界條件影響的不足，受到了國內外的廣泛關注。聲輻射力彈性成像主要可以細分為諧波運動成像(HMI)、剪下波彈性成像(SWEI)和聲輻射力脈衝成像(ARFI)等手段，這裡分別對它們作簡要介紹。

圖12 慢性肝病患者的肝臟剪下波彈性成像及定量分析圖。下圖是原始的成像圖，上圖的藍色區域則是在成像區域內選取直徑為3 mm的圓形定量檢測區域進行彈性模量的檢測

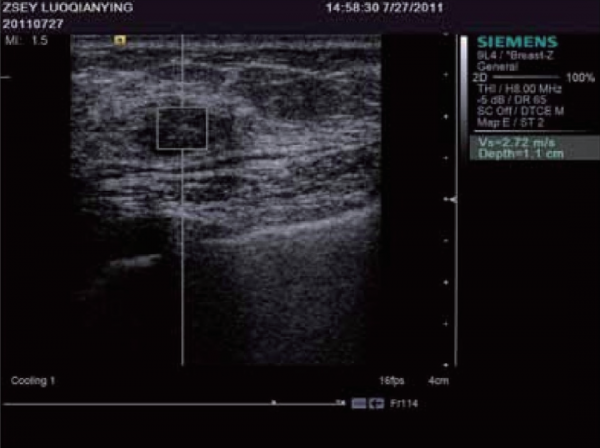
諧波運動成像最早由Maleke等人提出。透過探頭產生的超聲波對組織施加週期性的聲輻射力，使組織產生諧波運動。透過獲取組織被激發前後的B超影象並對其進行運動估計，可以間接反映組織的彈性狀況。該方法可以準確反映深部組織的區域性彈性狀況，但由於需要在激發訊號的同時監測組織的運動，因而採集到的B超訊號容易受到激發訊號的嚴重干擾，這是該成像方法迄今為止尚未得到完美解決的主要問題。當聲輻射力作用在組織上時會激發出剪下波，剪下波彈性成像正是透過檢測這一剪下波的傳播來達到成像的目的，最早由美國學者Sarvazyan和Emelianov提出。他們利用高強度聚焦超聲探頭產生聲輻射力，在人體組織中產生了明顯的剪下波，並運用磁共振成像方法監測該剪下波的傳播情況。由於剪下波速與人體組織的粘彈特性緊密相關，因此透過檢測剪下波的傳播速度等引數可以獲取組織的彈性資訊。圖12顯示了某一慢性肝病患者的肝臟彈性成像圖。聲輻射力脈衝成像技術最早由杜克大學的學者Nightingale等人提出，該方法透過高能聚焦超聲探頭在區域性組織中產生短暫的高強度聲輻射力，從而推動組織產生一定的應變，再透過追蹤這些微小應變和剪下波的傳播來判斷組織的粘彈特性。研究人員發現，組織對於脈衝聲輻射力的瞬態響應直接相關於區域性區域的硬度大小，而透過求解亥姆霍茲方程的反問題方法可以量化組織中剪下波的波速。Nightingale等透過詳細的數值模擬和體模研究證實了聲輻射力脈衝成像的可行性，並得到了與傳統B超影象相比更高的對比度和分辨力。如今的聲輻射力脈衝成像已在臨床上具備多種臟器檢查的能力，圖13顯示了某位良性纖維瘤患者的乳腺聲輻射力脈衝成像圖。

圖13 乳腺良性纖維瘤患者的聲輻射力脈衝成像圖

基於聲輻射力的彈性成像技術是對傳統準靜態彈性成像技術的重大突破，使得彈性成像對較深部位或有區域性遮擋的組織器官也有了一定的用武之地，在離體成像實驗和臨床診斷治療中均顯示了良好的應用前景。當然，如何提升成像速度、改善成像質量、確保劑量安全性也是亟待解決的重要問題。隨著技術的不斷髮展，相信聲輻射力彈性成像技術將會在不久的將來更好地造福人類。

6 聲輻射力天平

聲學中，我們將聲源在單位時間內向外輻射的聲能量定義為聲功率。超聲功率的測量是聲學研究中的熱點問題，對評估超聲裝置的安全風險、控制超聲裝置的輻射劑量、確保超聲診斷和治療過程的可控性與安全性有著重要意義。目前，關於聲功率的測量方法主要有聲輻射力法、聲光法、量熱法等，其中聲輻射力法是國際電工委員會(IEC)推薦的首選測量方法，也是目前唯一國際公認的標準方法。早在1976年，波蘭科學院的Zieniuk和英國薩里大學的Chivers就對聲輻射力法和量熱法進行了詳細的比較分析，認為前者的適用範圍更廣、測量更加簡潔有效。

圖14 利用全吸收靶(左)和全反射靶(右)測量聲功率的實驗裝置示意圖

利用聲輻射力測量聲功率的裝置被稱為聲輻射力天平。對於小振幅聲波而言，在橫向尺寸不受限制的行波傳播方向上，兩種介質的分介面或聲場不均勻處存在單向的穩態聲輻射力。事實上，這一壓力正是前文所述的朗之萬聲輻射力，單位面積上的聲輻射力稱為聲輻射壓。對理想的平面行波而言，聲輻射壓和聲強、波速存在關係：

其中，是聲波的能量密度。在測量中，將全反射靶或吸收靶放置於水中聲場裡感知聲能流，並用天平來精確測量此時靶受到的聲輻射力。最後，將聲輻射力換算成聲功率即得到最終的測量結果。圖14給出了利用全吸收靶和全反射靶測量聲功率的實驗裝置示意圖。全反射靶和全吸收靶的主要區別在於靶的結構特性不同。全反射靶通常是用薄金屬皮製成的中空凸圓錐體，其錐角為90°，它能將接收到的超聲波能量幾乎完全反射回去。全吸收靶的表面則是由許多鋸齒形吸聲尖劈排列而成，從而能夠吸收絕大部分的聲能量。圖15顯示了兩種靶的實物照片。對於全吸收靶測量而言，聲功率和輻射天平的讀數滿足關係= ，其中是測量當地的重力加速度；對於全反射靶測量而言，上述關係變為= /(2cos)，其中是聲束在圓錐形全反射靶上的入射角。當然，在聲吸收不可忽略時，我們還應當計及聲波在水中的吸收聲衰減。

圖15 全吸收靶(左)和全反射靶(右)的實物照片

2012年，上海交通大學壽文德等人提出利用聲輻射力天平測量電聲器件引數的方法，並給出了平面活塞型、球面聚焦型和圓柱面聚焦型換能器的實驗測量結果。近年來，他們又提出一種基於凸球面吸收靶的聲輻射力天平測量方法，成功測量了相控陣換能器的發射功率。2013年，北京理工大學沈洋等人首次針對平板傾斜放置時的聲輻射力天平測量裝置進行了詳細的分析，給出了理論計算結果和相應的實驗驗證，大大簡化了對傳統聲輻射力天平測量的實驗要求。2014年，黃鴻鑫等人利用聲輻射力天平法制成了聲功率測量儀。

7 結束語

聲輻射力既是聲場傳遞動量的反映，也是聲波非線性的重要體現。歷經了一個多世紀的探索與發展，關於聲輻射力的研究仍然方興未艾。一方面，不少學者已經給出了各種模型下聲輻射力的大量計算結果，為實際的聲操控提供了必不可少的理論基礎。另一方面，寬頻聲場的動態聲輻射力、多粒子的聲輻射力和血管壁等複雜邊界下的聲輻射力等成為了新的熱點，使得聲輻射力的基礎理論研究與實際操控結合得更加緊密。同時，隨著聲渦旋理論的發展，基於軌道角動量的聲輻射力矩開闢了新的聲操控自由度，讓這一領域更加呈現出生機盎然的發展前景。

在生命科學、材料科學、奈米科學等領域，對微觀粒子的無損精準操控已經成為不可或缺的核心技術。隨著這一技術的不斷髮展，人們已經不僅僅滿足於根據固定的聲場資訊來操控特定微粒，而是試圖面向特定應用場景、根據不同的操控需求反演所需要的聲場結構和操控系統，實現對操控物件的實時精準操控。在影象反饋技術和控制技術的輔助下，聲操控正逐漸走向微型化、自動化與智慧化。另一方面，物體的複雜動力學特性暗含了其本身的物理引數資訊，利用聲輻射力反演其物性引數對精準操控和非接觸測量有重要的理論指導意義。作為聲操控的物理基礎，聲輻射力這隻看不見的“手”也將會在眾多領域中有更多用武之地。

參考文獻

[1] Hasegawa T，Saka K，Inoue N et al. J. Acoust. Soc. Am.，1988，83：1770

[2] King L V. Proc. Roya. Soc. London Ser. A，1934，147：212

[3] Awatani J. J. Acoust. Soc. Jpn.，1953，9：140

[4] Yosioka K. Acta Acust. United Ac.，1955，5：167

[5] Yosioka K，Hasegawa T，Omura A. Acustica，1969，22：145

[6] Hasegawa T，Yosioka K. J. Acoust. Soc. Am.，1969，46：1139

[7] Hasegawa T，Watanabe Y. J. Acoust. Soc. Am.，1978，46：1733

[8] Hasegawa T. J. Acoust. Soc. Am.，1979，65：32

[9] Wu J R，Du G H. J. Acoust. Soc，Am.，1990，87：997

[10] Marston P L. J. Acoust. Soc. Am.，2006，120：3518

[11] Marston P L. J. Acoust. Soc. Am.，2009，125：3539

[12] Mitri F G. Ann. Phys.，2008，323：2840

[13] Mitri F G. Ultrasonics，2009，49：794

[14] Mitri F G. J. Phys. A：Math. Theor.，2009，42：245202

[15] Mitri F G. Eur. Phys. J. E，2009，28(4)：469

[16] Silva G T. J. Acoust. Soc. Am.，2011，130：3541

[17] Baresch D，Thomas J，Marchiano R. J. Acoust. Soc. Am.，2013，133：25

[18] Sapozhnikov O A，Bailey M R. J. Acoust. Soc. Am.，2012，133：661

[19] Silva G T. IEEE Trans. Ultrason. Ferroelectr. Freq. Control，2015，62：576

[20] Wang J，Dual J. Ultrasonics，2012，52：325

[21] Qiao Y P，Zhang X F，Zhang G B. J. Acoust. Soc. Am.，2017，141：4633

[22] Qiao Y P，Zhang X F，Zhang G B. Wave Motion，2017，74：182

[23] Qiao Y P，Shi T Y，Zhang X F. Wave Motion，2018，83：111

[24] Hasheminejad S M，Sanaei R. J. Comput. Acoust.，2007，15：377

[25] Mitri F G. Ultrasonics，2016，66：27

[26] Mitri F G. J. Appl. Phys.，2015，118：214903

[27] Mitri F G. Wave Motion，2015，57：231

[28] Mitri F G. EPL，2015，112：34002

[29] Mitri F G. Ultrasonics，2017，74：62

[30] 王明升，歐陽傑，劉浩 等. 應用聲學，2020，39：550

[31] Zang Y C，Lin W J，Su C et al. Chin. Phys. B，2021，30：044301

[32] Zang Y C，Lin W J. Results Phys.，2020，16：102847

[33] Cai F Y，Meng L，Jiang C X et al. J. Acoust. Soc. Am.，2010，128：1617

[34] 孫秀娜，張小鳳，張光斌 等. 陝西師範大學學報(自然科學版)，2015，43：28

[35] Lee J W，Ha K L，Shung K K. J. Acoust. Soc. Am.，2005，117：3273

[36] Gor′kov L P. Sov. Phys. Doklady，1962，6：773

[37] Kundt A. Ann. Phys. Chem.，1866，127：497

[38] Hanson A R. Rev. Sei. Instrum.，1964，35：1031

[39] Whymark R R. Ultrasonics，1975，13：251

[40] Hatano H. IEEE Trans. Ultrason. Ferroelectr. Freq. Control，1994，41：772

[41] Jackson D P，Chang M H. Am. J. Phys.，2021，89：383

[42] Xie W J，Cao C D，Lu Y J et al. Phys. Rev. Lett.，2002，89：104304

[43] Ashkin A. Phys. Rev. Lett.，1970，24：156

[44] Ashkin A，Dziedzic J M. Appl. Phys. Lett.，1971，19：283

[45] Ashkin A，Dziedzic J M. Science，1975，187：1073

[46] Ashkin A，Dziedzic J M. Science，1987，235：385

[47] Ashkin A. Proc. Natl. Acad. Sci. USA，1997，94：4853

[48] Wu J R. J. Acoust. Soc. Am.，1991，89：2140

[49] Shi J J，Daniel A. Lab Chip，2009，9：2861

[50] Li S. Anal. Chem.，2013，85：5468

[51] Lee J，Teh S Y，Lee A et al. Appl. Phys. Lett.，2009，95：073701

[52] Lee J W，Lee C Y，Shung K K. IEEE Trans. Ultrason. Ferroelectr. Freq. Control，2010，57：2305

[53] Lee J W. Biotechnol. Bioeng.，2011，108：1643

[54] Ma Z，Collins D J，Guo J et al. Anal. Chem.，2016，88：11844

[55] Chen X Y，Lam K H，Chen R M et al. Biotechnol. Bioeng.，2017，114：2637

[56] Zhao L R，Kim E S. Focused ultrasound transducer with electrically controllable focal length. Proceedings IEEE Micro Electro Mechanical Systems，2018：1088

[57] Marzo A，Drinkwater B W. PNAS，2019，116：84

[58] 梁彬，程建春. 物理，2017，46：658

[59] Maidanik G. J. Acoust. Soc. Am.，1958，30：620

[60] Zhang L K，Marston P L. J. Acoust. Soc. Am.，2011，129：1679

[61] Zhang L K，Marston P L. Phys. Rev. E，2011，84：065601

[62] Zhang L K，Marston P L. J. Acoust. Soc. Am.，2011，129：2381

[63] Demore C E M，Yang Z Y，Volovick A et al. Phys. Rev.Lett.，2012，108：194301

[64] Silva G T，Lobo T P，Mitri F G. EPL，2012，97：54003

[65] Mitri F G. Phys. Rev. E，2012，85：026602

[66] Mitri F G，Lobo T P，Silva G T. Phys. Rev. E，2012，86：059902

[67] Zhang L K. Phys. Rev. Appl.，2018，10(3)：034039

[68] Gong Z X，Marston P L. Phys. Rev. Appl.，2019，11：064022

[69] 臧雨宸，林偉軍，蘇暢 等. 聲學學報，2021，46：92

[70] Zang Y C，Lin W J，Zheng Y F et al. J. Sound Vib.，2021，509：116261

[71] Wang T，Ke M，Li W et al. Appl. Phys. Lett.，2016，109：123506

[72] Zhang R Q，Guo H L，Deng W Y et al. Appl. Phys. Lett.，2020，116：123503

[73] Hong Z，Zhang J，Drinkwater B W. Phys. Rev. Lett.，2015，114：214301

[74] Jiang X，Zhao J J，Liu S L et al. App. Phys. Lett.，2016，108：203501

[75] Ophir J，Cespedes I，Ponnekanti H et al. Ultrasonic Imaging，1991，13：111

[76] Maleke C，Konofagou E E. Phys. Med. Bio.，2008，53：1773

[77] Sarvazyan A P，Rudenko O V，Swanson S D et al. Ultrasound Med. Bio.，1998，24：1419

[78] 曾婕，吳莉莉，鄭榮琴 等. 中華超聲醫學雜誌，2012，9：781

[79] Nightingale K，Soo M S，Nightingale R et al. Ultrasound Med. Bio.，2002，28：227

[80] 歐冰，羅葆明，智慧 等. 中國醫療器械資訊，2012，6：18

[81] Zieniuk J，Chivers R C. Ultrasonics，1976，14：161

[82] 楊德俊，陳沈理，何卓斌 等. 電子質量，2018，7：90

[83] 壽文德，餘立立，胡濟民 等. 聲學技術，2012，31：107

[84] 壽文德，賈龍洋，吉祥 等. 聲學技術，2019，38：629

[85] 沈洋，胡亞琴，胡毅. 科協論壇，2013，12：201

[86] 黃鴻新，徐紅蕾，胡昌明 等. 實驗技術與管理，2014，31：79

不代表中科院物理所立場

編輯：fiufiu