多年前,網上流傳著一個經典的段子
“小明,聽說你大學的專業是流體力學?”
“是的,領導。”
“那好,去幫我倒杯水。”
“領導,請你尊重這門專業,流體力學是……”
“請你談談非等熵的穩態可壓磁流體力學方程在持續等離子體約束受控熱核聚變中的應用。”
“領導,飲水機在哪?”
哭笑不得之際,我們不禁要問,流體力學到底是幹啥的?難道流體力學專業的娃兒只能給領導端茶倒水嗎?
作為力學的重要分支,流體力學主要研究在各種力的作用下,流體的狀態、運動規律以及流體與外界的相互作用。地球人對流體都不陌生,我們呼吸的空氣、喝的水,都是流體。那麼流體力學研究中又是如何分類流體的呢?
理想流體 VS 實際流體
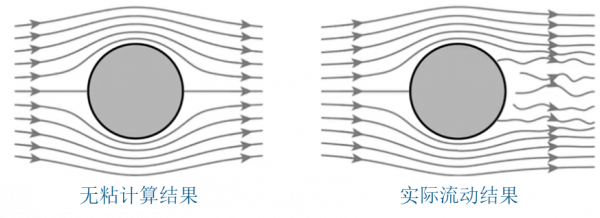
自然界中的流體都有粘性,統稱為粘性流體或實際流體。比如我們攪拌蜂蜜時會感受到粘滯的作用,而飛機飛行所受的阻力也很大程度上來源於空氣的粘性。由於實際流體的粘性,使得流體運動的研究變得非常複雜。為了便於理論分析,在流體力學中引進了“理想流體”的概念。理想流體就是沒有粘性的流體,當然這是一種假想的流體,實際中並不存在。但研究無粘流體的運動,可以使問題大大簡化,容易得到流體運動的基本規律。
對某些粘性影響不大的流動問題,忽略粘性所得到的結果與實際結果往往差別不大。而對於必須考慮粘性作用的流動問題,除了使用更典型的有粘方法,也可專門對粘性作用進行分析,然後再對理想流體的結果進行修正和補充。
牛頓流體 VS 非牛頓流體
那麼流體的粘性和什麼有關呢?
作為世界物理學界Top2的男人,牛頓除了被蘋果砸到,發現各種牛X定理,霸屏整個中學物理課本之外,連流體也不肯放過。經過大量的實驗研究,牛頓於1686年提出了著名的“牛頓內摩擦定律”——流體的內摩擦力(即粘性力)的大小與流體的性質(粘性係數μ)有關,並與流體的速度梯度和接觸面積成正比。
大量實驗證明:大多數氣體、水和許多潤滑油都能很好的遵循上述的牛頓內摩擦定律,即當壓力和溫度一定時,流體的內摩擦應力與速度梯度成正比。這種滿足牛頓內摩擦定率的流體稱為牛頓流體。需要指出的是,儘管我們平時接觸到的大部分流體都是牛頓流體,仍有一些流體比如生物流體、高分子聚合物的濃溶液等,不能遵循牛頓內摩擦流體,稱為非牛頓流體。
連續介質 VS 非連續介質
我們知道,N-S方程描述了基於連續介質假定的牛頓流體的動量守恆。“連續”是一個比較直觀的概念——“剪不斷,理還亂”,正如我們宏觀所見的流體。不過在流體力學層面,有一個無量綱數可以作為衡量連續與否的標識——這便是努森數(Kn),其定義為分子平均自由程長度與典型的物理尺度之比。
基於努森數的定義可以知道,努森數越大,意味著物理尺度和分子平均自由程越接近,分子的離散效應越強,研究中越不能忽略分子之間複雜的作用力;反之,努森數很小,意味著物理尺度遠遠大於分子自由程,不再關注分子團內部的相互作用,轉而研究其宏觀狀態的密度、速度、壓力等參量。
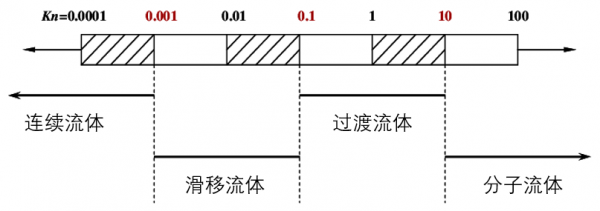
下圖給出了基於努森數定義的流體狀態,其中Kn小於0.001,則認為流體滿足連續介質的假設。常溫常壓下的分子平均自由程約為70nm,由此可以估算自然環境下,0.07mm的物理尺度即可滿足連續介質假設,因此工程上絕大部分的流動問題都可以認為是連續流體,滿足N-S方程的前提條件。
對於努森數足夠大的流體,比如極稀薄氣體,可以直接使用分子動力學進行描述,利用漢密爾頓方程求解。而二者之間還有滑移流體和過渡流體等不同的類別,分別對應有專門的描述方法。
熱動平衡 VS 非熱動平衡
除了上面提到的牛頓流體、連續介質假定兩個前提條件,N-S方程還有一個侷限——它只適用於大尺度的緩變行為,也是我們通常所說的“熱動平衡”或“準熱動平衡”的狀態,此時分子的熱動鬆弛時間(恢復到區域性熱動平衡的時間)遠遠小於宏觀尺度。現實中大部分流動問題都屬於這兩類。而非熱動平衡狀態,比如衝擊、爆炸等,宏觀流動的特徵時間也極短——以至於分子的熱動鬆弛不可被忽略。
尤拉法 VS 拉格朗日法
說完了實質,再看看形式——流體力學的兩種主要描述方式:拉格朗日法和尤拉法。
在經典場論中,拉格朗日法(又稱體系法)是研究流場內個別流體質點在不同時刻的位置、流速、壓力等引數的變化。也就是用隨時間的變化來描述流體質點的運動引數,各質點運動狀況的總和就構成了整個流體的狀態。
尤拉法(又稱控制體法)是研究整個流場內不同時刻,不同位置上的流體質點的引數。它把注意力集中在選定的空間點上而不是選定的流體質點上。因此,尤拉法確定的是佔據流場中的全部流體質點的瞬時流動引數。
為了更形象的對比尤拉法和拉格朗日法,小編整理了上面這幅圖:拉格朗日法就好像是跟在鴨子後面划船,而尤拉法則更像是在站在橋上數多少鴨子游過去。需要特別說明的是,最早提出這兩類研究流體方法的人都是尤拉。
N-S方程 VS 玻爾茲曼方程
前面鋪墊了這麼多,目的還是把玻爾茲曼這尊大神娓娓的請出來。當然在此之前,還有必要先來捋一捋經典力學描述流體的方式。
流體的基本方程本質上是質量、動量和能量守恆方程,而N-S方程只是在宏觀上基於連續介質假定,利用偏微分方程描述粘性流體流動的運動方程,僅僅是流體基本方程的一種表達方式。而N-S方程反映的就是牛二定律F=ma。我們先來回顧一下用尤拉法描述的N-S方程的推導過程:
除了上述的動量方程之外,我們同樣可以推導微分形式的質量和能量守恆方程,此處不再贅述。而反觀另外一種描述流體運動的玻爾茲曼方程,則會看到一種完全不同的奧妙。
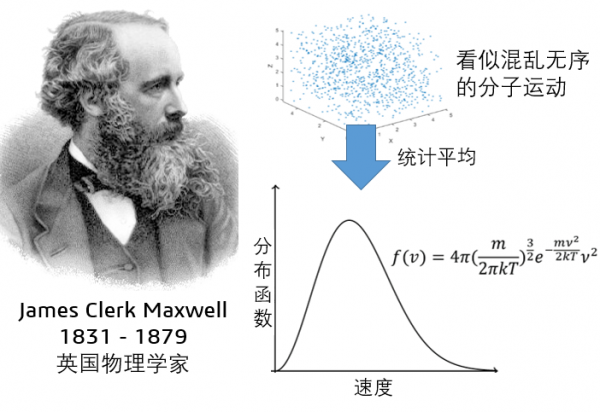
1859年,麥克斯韋發現在宏觀系統中追蹤每個分子的運動軌跡難以實現,於是產生了統計平均的概念。麥克斯韋認為,任意時刻單個分子的速度和位置資訊並不重要,分佈函式才是描述分子效應的重要引數。速度分佈函式給出了在某一給定時間,速度在一定範圍內的分子在整個系統中所佔的百分比。當氣體處於熱動平衡狀態時,氣體將均勻的分佈,而唯一的未知量就是速度分佈函式。
這種方法並非直接描述流體的速度、壓力等宏觀變數,也非直接描述每個流體分子的微觀運動,而是用統計的方法描述空間內流體粒子的速度分佈。其描述方式介於宏觀和微觀之間,被稱之為介觀。玻爾茲曼更進一步將麥克斯韋分佈推廣到任意大系統,他第一個認識到熵的熱力學概念和大系統狀態的統計分析之間的緊密聯絡,即宏觀變數中系統的熵隨著時間增大,與微觀分子排列的最大可能數相對應。
聽不懂,聽不懂,聽不懂,說人話!
老話說:不患寡而患不均,不均就會出問題,打土豪啊分田地。
任意大系統雖然不像麥克斯韋的描述那麼平均,但會趨向於平均。比如我們用活塞將盒子內的分子都壓到一側,鬆開活塞後,分子將迅速擴充套件到整個盒子空間並趨於均勻分佈。
對於這樣的過程需要有更詳細的數學描述。於是,玻爾茲曼輸運方程及其質量、動量和能量守恆方程便呼之欲出了。透過這些方程先求解出粒子的介觀分佈,進而可推匯出宏觀屬性。
至此,我們可以對玻爾茲曼眼中的流體力學做個總結:使用拉格朗日方法觀察處於介觀尺度下的流體粒子的分佈規律,並使用統計學思路研究其輸運與守恆,並透過積分將介觀的速度分佈函式和宏觀的物理量建立聯絡。
也許,很少有人關注細小砂礫的運動,而它恰恰是形成各種複雜山體結構的本源。如果說傳統CFD方法是“透過外表看現象”,那麼LBM方法則更像是“透過本質看現象”。
N-S方程的數值方法 VS LBM
無論是N-S方程還是玻爾茲曼方程,都是描述流體運動的解析方法。面對實際問題複雜的邊界和初始條件,最終還是要回歸到離散求解的數值方法。
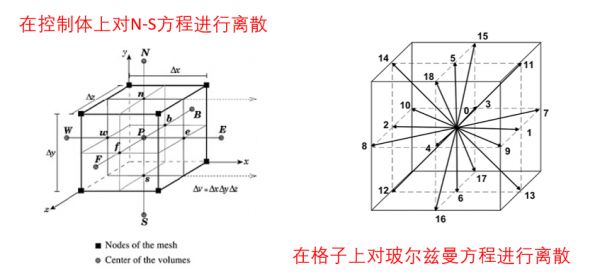
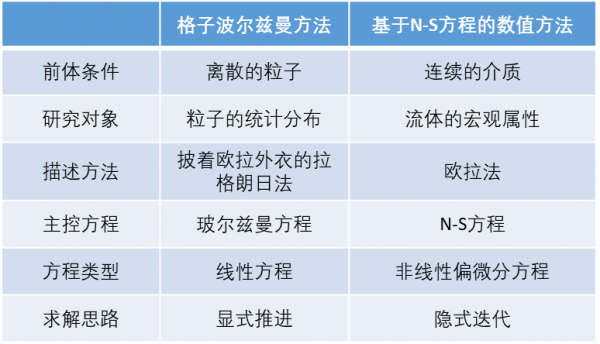
對於N-S方程的數值求解,最常規的有限體積法(FVM)的思路就是在流體域的每個離散控制體網格上分別施加方程進行求解;格子玻爾茲曼方法(LBM)同樣也是在格子上對玻爾茲曼方程進行時空的離散,只是對付這個簡單的線性方程,其數學處理要簡單的多。
當然,無論是LBM還是N-S數值方法的構建,都是可以看成對最基本的大量微觀粒子運動的合理粗化。如果只在離散的格子內研究其速度分佈函式,並將粒子的運動簡化為只沿有限個特定的方向,則演化為LBM;而基於連續的牛頓流體和近熱動平衡的假設,在有限的單元內研究流體的宏觀引數,則演化為N-S方程的數值方法。
兩種數值方法主要區別見下表,可見這是兩套完全不同的思路和實現方法。LBM雖是求解粒子的速度分佈,形式上是一種統計的方法,但其本質上仍是追蹤離散粒子的運動,最終獲取整個流場的粒子狀態,是一種比N-S方程更接近物理本質的描述。
國內外有很多學者專注於LBM方法,但研究大多集中在多相流或者稀薄氣體等傳統CFD軟體很難模擬的領域。事實上許多學者為了向世人證明LBM並不是天馬行空的猜想,使用嚴格的數學推導,基於LBM方程施加Kn數遠小於1的假設條件,推匯出了N-S方程。因此可以認為,N-S方程的描述是LBM在連續介質條件下的一個特例,而玻爾茲曼則為世人提供了一個更為接近物理本源的恢弘視角看待流體。
所以,LBM方法在傳統CFD的研究領域一樣擁有獨特的優勢,比如汽車和飛機的空氣動力學與氣動噪聲問題。或許這也可以給學者們在選擇LBM的應用領域上提供一些啟發和參考吧。
流體力學從入門到放棄,大概只需要一杯咖啡的時間。至此,相信小夥伴們可以放心大膽的向領導回覆:“領導,飲水機在哪?要不要給您泡點茶葉?”
-END-
來源:LBM與流體力學
原標題:玻爾茲曼眼中的流體力學
編輯:fiufiu