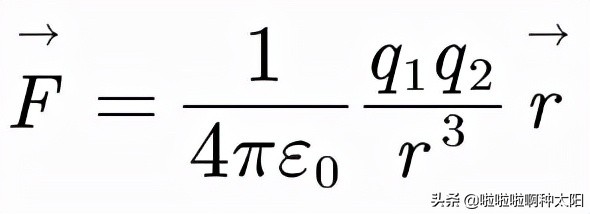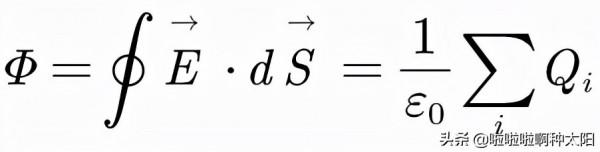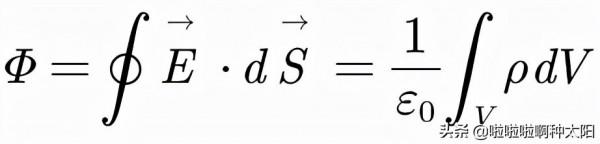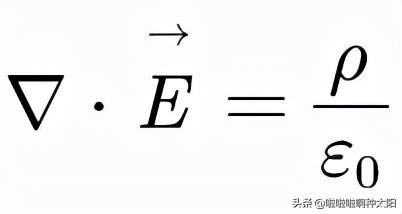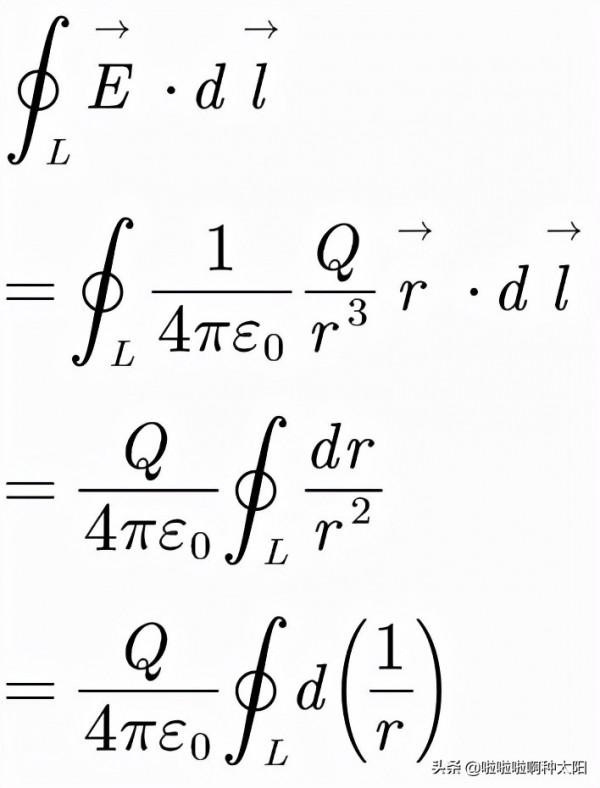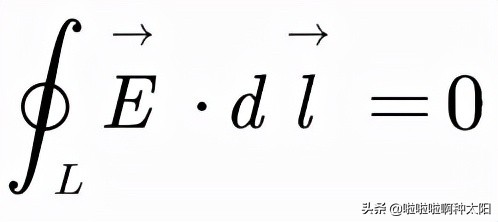電荷和電場
各位小夥伴如果喜歡的話多多關注、點贊、轉發哦,謝謝大家啦!
從這一期電動力學專題,我們將開始正式地對電磁世界進行探索,各位小夥伴請緊握扶手,我們出發咯!
(因為鹹魚作者本身是物理本科在讀,所以對一些內容掌握的也有所欠缺,更新不穩定是因為在寫的時候一些不熟練的地方還需要多看一下,物理很有趣但也需要嚴謹地對待,希望大家體諒一下,謝謝大家)
庫侖定律
1785年,庫侖透過實驗發現,真空中靜止點電荷Q對另一個靜止點電荷Q'的作用力F滿足:
其中,q1,q2分別為Q和Q'的帶電量,r為Q指向Q'的向量,其數值大小為Q到Q'的距離,ε0為真空介電常數,ε0≈8.85×10^-12 C²/N。
針對一對點電荷時,庫侖定律成立,那麼若是有多個點電荷同時存在時,會有什麼結果呢
實驗結果告訴我們,當有多個點電荷同時存在時,每一個點電荷受到的作用力為其他點電荷對其單獨的作用力的線性疊加,若該點電荷所帶電量為Q,那麼我們就能得到:
得到疊加原理之後,我們就可以很容易地處理一些連續帶電體的問題:
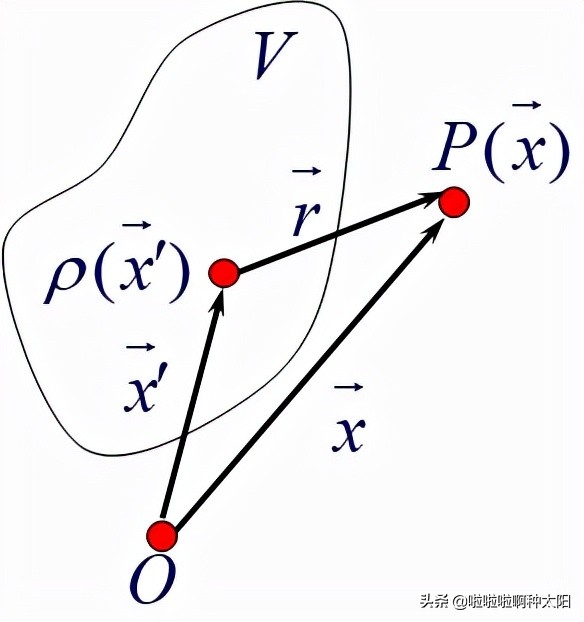
如圖,存在電荷連續分佈於空間某一區域V內,那麼我們可以取體積元dV',則在dV'內所含的電荷dQ等於該點的電荷密度ρ(⃗x')乘以dV',即:
假設P點的電荷所帶電荷量為q,那麼我們根據庫侖定律和疊加原理,就能得到靜電力的大小為:
庫侖定律是實驗定律,沒有解決電荷間作用力的物理本質問題。對之有不同的兩種物理解釋:(1)電荷之間是直接的超距作用;(2)電荷的相互作用是透過電場來傳遞的。我們不能單純由靜電現象判斷哪一種解釋是正確的。在運動電荷的情況下,兩種觀點就顯示出不同的物理內容。而實踐證明透過場來傳遞相互作用的觀點是正確的。
那麼這個“場”是什麼?從庫侖定律中我們可以看出,假如點電荷A帶電量一定,那麼對於點電荷B來說,它所受的靜電力的大小與它自身的帶電量成正比,於是我們就可以引入一個新的物理量:E=F/q
這裡的E與存在於該點的電荷並沒有什麼關係,而是表示空間中的其他電荷在此處產生的效果。我們就把E稱為電場。
我們根據定義很快就能得到點電荷產生的電場:
同理,對於連續帶電體產生的電場我們也有:
高斯定理和電場的散度
當我們得到電場之後,不可避免的,我們就想要去了解電場的影象是怎麼樣的,因此我們很自然的就想到了去看看電場的散度和旋度是怎麼樣的。
在高中物理中我們知道,電通量Φ=E·S,即電場強度乘以被電場線穿過的平面的面積。那麼假如我們有一個閉合曲面S包圍著點電荷Q,閉合曲面的面元為dS。很顯然,電場線以點電荷為源,向四面八方發散,從閉合曲面的角角落落傳出,我們根據電通量Φ=E·S便能很自然的得到點電荷產生的電場為面積分:
我們將E的表示式代入進行積分(dΩ為立體角元)就能得到:
假如電荷不在閉合曲面內,那麼電場線穿入閉合曲面後再穿出,對於閉合曲面的電通量沒有貢獻,因此Φ=0。
假如閉合曲面內有多個點電荷,顯然它們的電場線都將穿過閉合曲面,所以就有:
如果閉合曲面內電荷連續分佈在空間中,我們則可以得到:
其中,ρ是電荷密度,V是閉合曲面包圍的體積,顯然ρ的體積分就是V內總電荷量。這也是靜電場高斯定理的積分形式。
根據高斯公式我們知道,E的面積分等於E的散度的體積分,即E·dS=∇·EdV,假如我們讓V不斷縮小,最終我們就有:
這就是靜電場高斯定理微分形式,在這裡它的物理意義是說明:靜電場是一個有源場,電荷是電場的源點,電場線從正電荷出發到負電荷結束。
靜電場的旋度
接下來我們來探究一下靜電場的旋度∇×E,這個物理量表示的意思是靜電場是否有渦旋狀結構,簡單來說就是靜電場的電場線是不是會打轉。
我們首先來看一下由點電荷激發出的靜電場,其電場強度E對任一閉合迴路的環量,結合庫侖定律我們有:
最後這個積分的被積函式是一個全微分,而由於繞了閉合迴路L一圈以後,相當於又回到原點,函式1/r的值並未發生改變,所以我們就可以得到這個迴路積分的結果為零,因此,我們有:
我們成功證明了點電荷的電場環量為零;而對於多個點電荷形成的電場,由於每個點電荷的電場環量均為零,根據疊加原理我們可以得到總電場的環量也為零。
在這裡我們利用高數中學過的斯托克斯公式,根據斯托克斯公式我們可以給出:
我們把迴路L不斷縮小,最終我們可以得到:
這個式子告訴我們靜電場是一個無旋場,電場線並不會首尾相接地打轉。
下期預告
在下一期的電動力學專題中,我們將會簡單地瞭解電流和磁場,那麼它們又具有怎麼樣的性質呢?各位對電磁世界好奇的小夥伴,我們下期專題見啦,喜歡的話記得點一下關注哦!
編 輯|笨笨
校 對|笨笨
審 核|笨笨