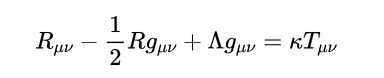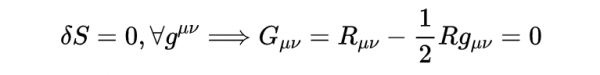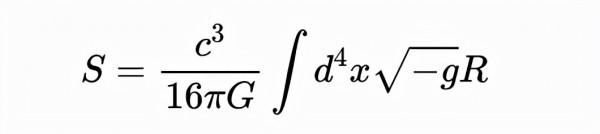在數學中，度規或距離函式是給出集合中每一對點元素之間的距離的函式。一個帶有度規的集合稱為度規空間。在微分幾何中，度規的一個重要來源是度規張量。度規張量允許透過積分來確定沿著曲線的距離，從而確定度規。

在廣義相對論中，時空是一個光滑的、座標友好型（coordinate-friendly）的空間，稱為流形（manifold）。度規g允許我們嚴格地定義這個流形中向量的距離和長度。我們把度規看成是一個矩陣，在流形上從點到點變化，解這個度規的方法是解愛因斯坦場方程。

那麼問題來了，在廣義相對論的框架內允許什麼樣的度規。一般來說，我們不可能寫下任何我們想要的度規。那麼，在自然界中哪些度規是被允許的？是否有一些方程式可以讓我們確定一個度規的演變？

事實證明，物理上允許的度規是愛因斯坦場方程的解。愛因斯坦的場方程如下：

在右手邊，符號T代表能量動量張量。能量動量張量編碼了大質量物體（比如中子星）在時空中的能量。

左邊包含了描述時空的關鍵屬性。R表示時空有多 "彎曲"。左邊的第一項是裡奇曲率，它描述了宇宙的三維空間與平坦空間相比是如何彎曲的（彎曲程度）。它有兩個希臘字母下標，因此它是一個2級張量（所以我們可以把它寫成一個矩陣）。第二項描述了與平坦空間相比，體積是如何扭曲的。符號R被稱為裡奇標量。第三個項是宇宙學常數，帶字母g的項是度規本身。

在這篇文章中，我想介紹一下這個方程是如何推匯出的。

愛因斯坦-希爾伯特作用

我們把度規當作一個動態的物理變數。首先透過在固定時間內對兩點間的拉格朗日積分來構造一個作用；然後，為了找到經典粒子的路徑，我們要找到使作用量最小的路徑。

為了在廣義相對論中做到這一點，我們將構建一個包含度規的作用。為了構建這個作用，必須想出一些合理的度規函式，然後測試所得到的運動方程是否與我們在經典情況下得到的一致。

一旦構建了一個作為度規函式的作用，我們就會嘗試將這個作用最小化，以求得確切的度規是什麼。由此得到的度規就是愛因斯坦場方程的解。將作用量最小化是一項技術上的挑戰，但是我們只需要做一次計算。

構建愛因斯坦-希爾伯特作用‍

我們把從度規中構建的作用稱為愛因斯坦-希爾伯特作用。我們唯一要處理的物件是度規g。一個物體的 "體積 "完全取決於時空中的距離是如何定義的。我們可以用度規來定義時空中的體積概念（取其行列式的平方根）。度規的行列式的平方根是我們可以使用的一個自然的體積形式。這就給了我們一個提示，作用看起來應該像：

現在，我們唯一能做的就是把裡奇標量提出來。裡奇標量是一個實數，在流形中的每一點上都有一個值。當裡奇標量在某一點為正時，如果有歐幾里得度規，圍繞該點的小球的體積比半徑相同的小球的體積要小。如果裡奇標量為負則相反。下面粉色的球是有度規g的球的體積，棕色球是用歐幾里得平面度規感知的體積。

因此，構建作用的自然方式是把裡奇標量放在體積形式的前面。這在下面的方程中顯示。裡奇標量用符號R來表示。

同樣，裡奇曲率張量也衡量空間的曲率與平坦空間的不同。

愛因斯坦-希爾伯特作用的極端‍

為了推匯出愛因斯坦場方程，我們需要找到使作用量最小的度規。為了做到這一點，我們將對度規進行微小的擾動，看看作用S如何變化。我們希望作用S會發生微小的變化，我嘗試寫出一個表示式來說明作用發生了多大變化。

在數學上，我們把一個微小的變化稱為 "擾動"。因此，為了擾動度規，在度規上增加一個微小的項。這個微小的項是用希臘的delta符號表示的。我們對度規的擾動看起來像：

當我們改變整個式子時，訣竅是把裡奇標量寫成裡奇張量與度規縮並的形式。然後，當看到一個很小的變化時，我們應用乘積法則，把所有的東西展開。我們必須記住體積的形式並且考慮當度規改變時體積的形式是如何變化的。

為了得到運動方程，我們需要處理積分中的項，從而分解出一個可以設為零的普通表示式。要做到這一點，需要簡化許多項，得到：

由字母X代表的張量是一個邊界。當我們對度規的任意變化施加平穩性的條件時，就得到了被積函式的一個條件。這就得到了真空愛因斯坦方程（因為我們假設沒有質量或能量）。

右邊的方程正是在沒有能量或質量的情況下的愛因斯坦場方程。但是，我們假設大部分的常數都是1。

加入基本‍常數‍

我們可以使用量綱分析來填充這裡的常數。作用S的量綱是ML^2/T，度規是無量綱的，而R的單位是1/L^2。我們需要作用是無量綱的，因此要在它前面加一些常數來平衡這些量綱。最後得到作用S是：

有了這些常數，我們就完全得到了愛因斯坦的場方程。