三百多年的跌跌撞撞,走走停停,懷爾斯最終結束了數學史上這場最為漫長的接力賽。看著費馬猜想被證明,終於可以被稱為費馬大定理,最不開心的恐怕是19世紀“數學界的無冕之王”希爾伯特了。當他還在世時,有人問他為什麼不證明費馬猜想,他曾反問:“為什麼要幹掉那隻下金蛋的老母雞呢?”在他看來,費馬猜想為人類數學界立下了汗馬功勞,很多數學家在證明費馬猜想時創立了許多新的數學理論。現在懷爾斯這個“兇手”幹掉了這隻“母雞”,不知道希爾伯特作何感想。
其實希爾伯特也不用傷心,因為這隻“母雞”即使被證明了,到今天仍能夠孵蛋。其中,橢圓曲線就是那顆“金蛋”。2008年,費馬大定理在非對稱加密領域再現神蹟。密碼學朋克們將橢圓曲線加密法(ECC)應用於比特幣,使比特幣成為數學上牢不可破的“數字黃金”,開創了密碼安全史上的新篇章。
作為一種非對稱加密技術,ECC利用橢圓曲線等式的特殊性質來產生金鑰,而不是採用傳統的方法,即利用大質數的積來產生。相比之下,基於大整數因子分解2問題的RSA演算法3,有著單位長度較長,計算效率低等缺點;而作為因子的兩個素數若長度越短,被反破解的可能就越大。另外,黎曼猜想一旦得證,還可能派生出攻擊RSA公鑰加密演算法的規律。
而ECC克服了RSA演算法的一些缺陷,其執行機制非常巧妙,將加密問題轉換為橢圓曲線方程在有限域中的阿貝爾群,從而利用群論中阿貝爾群計算問題,採取公私鑰和雙金鑰相結合的方式進行加密或解密。
橢圓曲線通常用E表示,常用於密碼系統的基於有限域GF(p)上的橢圓曲線是由方程:
y² = x³+ax+b(mod p)
所確定的所有點(x,y)組成的集合,外加一個無窮遠點O。其中a,b,x,y均在GF(p)上取值,且有4a³+27b²≠0,p是大於3的素數。通常用Ep(a,b)來表示這類曲線。
對比常見的橢圓曲線方程y²=x³+ax+b,會看到這只是對原式進行了簡單的取模處理,但以橢圓曲線y²=x³-x+1的影象為例,圖3-1是y²=x³-x+1在實數域上的橢圓曲線。
圖3-1實數域上的y²=x³-x+1
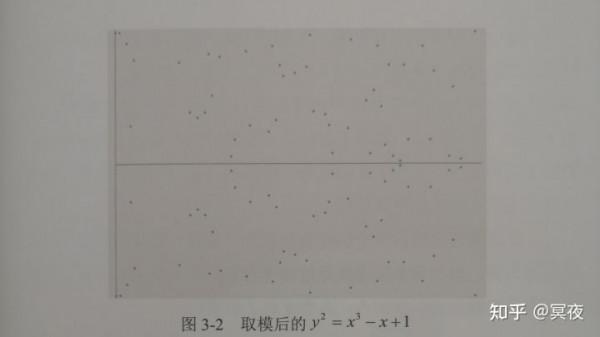
圖3-2則是橢圓曲線y²=x³-x+1對素數97取模後的影象。
顯然,相比於圖3-1,會發現引入有限域上的橢圓曲線圖3-2基本已面目全非,原本連續光滑曲線上的無限個點變成了離散的點,不過依然可以看到它是關於某條水平直線y=97/2對稱的。而這正符合密碼學所要求的有限點和精確性。
目前,尚不存在多項式時間演算法求解橢圓曲線上的離散對數問題,因而建立在求解離散對數問題困難性上的橢圓曲線密碼體系(ECC)安全性極高,其地位已逐步取代RSA等其他密碼體系,成為密碼學的新生巨星,是日後非常重要的主要公鑰加密技術。
結語:358年孵蛋的意義
數學家們花了幾百年證明費馬大定理有意義嗎?
多少世紀以來,不斷有數學家向“不可能”的費馬大定理發出戰書,有的因為能力有限早早放棄,有的傾其一生也只看清楚一鱗半爪,最終連萬能的計算機也無可奈何。
在這個過程中,很多人都知道,也許一年又一年地耗下去依然得不到一個結果,成千上萬個方程可能也得不出一個解。但他們最終還是向永恆發起了挑戰,即使計算機已宣佈放棄,這些人依然覺得自己可以解決這個難題,這就是人類的堅強和韌性。
回望這三百多年,人類每一次都用盡全力地追尋,雖然未能抵達終點,卻擴充了“整數”的概念,擴充套件了“無窮遞降法”、虛數和群論的應用,催生出庫默爾的“理想數論”,促成了莫德爾猜想,證明了谷山一志村猜想,加深了對橢圓方程的研究,找到了微分幾何在數論上的生長點,發現了伊利瓦金-弗萊切方法與伊娃沙娃理論的結合點,推動了數學的整體發展……
一部波瀾壯闊的數學史由此徐徐展開,這是一場智者征服世間奧秘的接力賽,而信仰和追尋就是這場接力賽的最大意義。畢竟,正是因為有了一群仰望星空的人,人類才有了希望。
感悟:知識即是力量有是財富!一個費馬大定理,不說其他成果,僅催生出的比特幣就讓無數人為之痴迷!這358年是智者的追求,文明的發展。在現在這樣生活安定,教育公平,知識獲取方便的時代,我們更應該注重教育,為人類文明的進步提供一份力量!