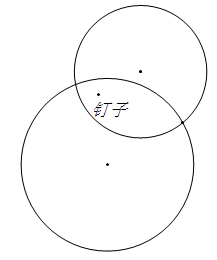今天去拜訪一個朋友,就是管著許多許多鑰匙,需要這種東西的朋友。
他那裡這種鑰匙盤可不是一個兩個,而是一大摞,大的小的全有。
我知道你想什麼,你想多了,我哪有那麼有錢的朋友,他只是宿管而已。
朋友去查寢,我就拿著鑰匙盤玩。
牆上有釘子,我就把鑰匙盤一個個掛到一個釘子裡去。
一個鑰匙盤當然可以掛好,兩個鑰匙盤掛上去,就可以隨意調整它們的位置了。
比如這樣掛
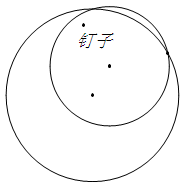
也可以這樣掛
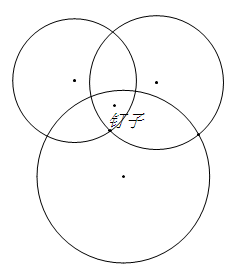
三個鑰匙盤掛上去,比如這樣
我發現,三個鑰匙盤的時候,我總可以擺出一個位置,使得每個圓的圓心都不被覆蓋。
再加一個鑰匙盤,4個鑰匙盤也是可以想辦法讓每個圓的圓心露出來,5個鑰匙盤就比較難了,不過,經過不太難的嘗試,還是讓我擺出來了。
然後是6個,我擺了一個多小時,也沒辦法讓每一個圓心都露出來,至少有一個圓心會被其他圓覆蓋。
真是邪了門了,我就不信邪,又拿了更多大大小小的鑰匙盤,反正宿管有的是鑰匙盤,擺了一晚上。
最後,朋友查寢回來,喝酒,吹牛,然後繼續喝酒,然後繼續吹牛,然後,然後就斷片了。
等酒醒,完了,已經沒有鑰匙盤可以擺弄了,不能繼續嘗試了。
那麼,只好拿出數學人的本份,能不能從數學角度找到一個位置,使得6個鑰匙盤掛在一個釘子上,同時每一個圓心都不被覆蓋呢?
不能。
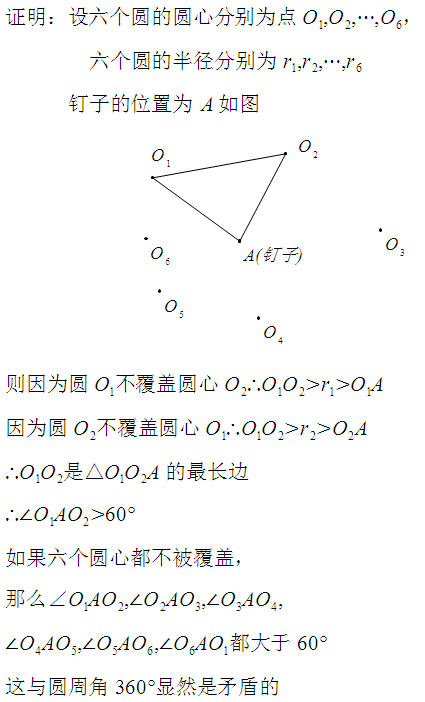
那麼能不能證明不能,或者說,能不能證明6個鑰匙盤掛在一個釘子上,至少有一個圓心會被其他圓覆蓋?
……
思考中
……
寫寫畫畫
……
繼續思考
……
繼續亂寫亂畫
……
上電腦,幾何畫板
……
繼續亂寫亂畫,胡思亂想
……
叮咚,我會證明了。
所以,六個圓,無論怎麼釘,都至少有一個圓心會被覆蓋。
明白之後,再無去擺弄鑰匙盤的興趣,除非。。。上面的鑰匙裡,有幾把是我的房。
(醒醒,窮教書的,想什麼呢!)