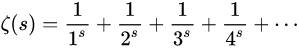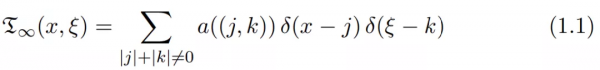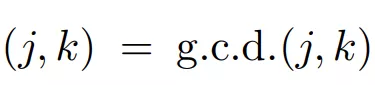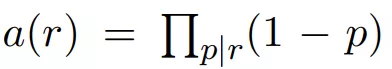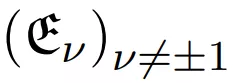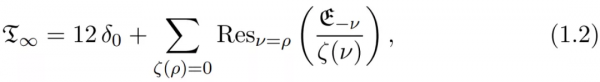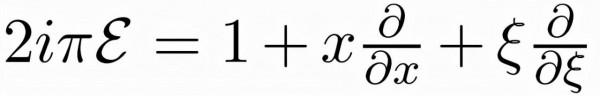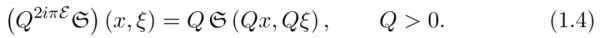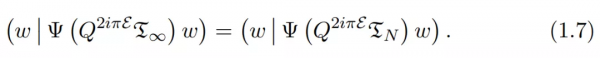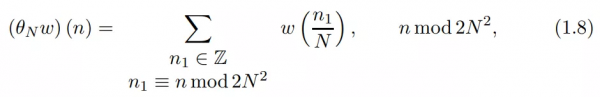機器之心報道
機器之心編輯部
暫時看不懂,但還是大受震撼。
2018 年秋天,當菲爾茲獎、阿貝爾獎得主、89 歲高齡的邁克爾 · 阿蒂亞(Michael Atiyah)爵士站在海德堡獲獎者論壇的講臺,用 45 分鐘、一頁 PPT 展示了自己對黎曼猜想的證明時,眾人沸騰。
這是阿蒂亞爵士的最後一次公開數學報告,報告結束後三個月,阿蒂亞爵士與世長辭。
擁有有 160 多年曆史的黎曼猜想,是數學王冠上的明珠,讓無數人為之輾轉。
試圖證明這一猜想的人很多,但被公認的方法至今還沒出現。阿蒂亞爵士在演講之後也公佈了自己證明黎曼猜想的預印本,仍未被眾人認可。
近日,一份關於黎曼猜想證明的預印本論文,在數學社群引發了熱議。
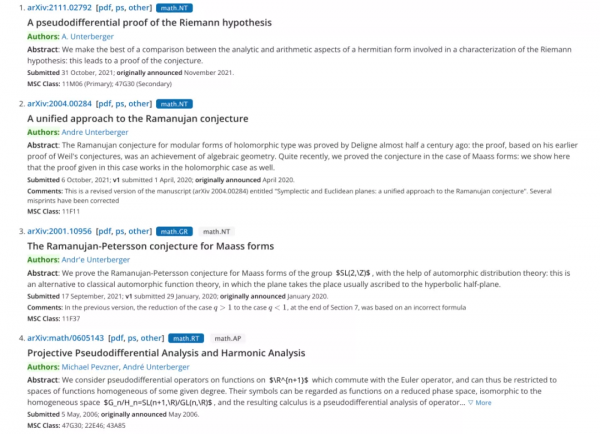
10 月 31 日,蘭斯大學的 Andre Unterberger 在 arXiv 上傳論文《A pseudodifferential proof of the Riemann hypothesis》。
論文地址:https://arxiv.org/pdf/2111.02792.pdf
作者 1971 年在巴黎狄德羅大學獲得博士學位,研究方向為偏微分方程。他的導師是法國數學家、1950 年菲爾茲獎得主 Laurent Schwartz。
2002 年,Andre Unterberger 獲得西班牙 Ferran Sunyer i Balaguer 獎。此前,他也曾發表過關於拉馬努金猜想、龐加萊猜想等數學命題的證明,並出版了多本著作。
這篇論文的參考來源也是 Andre Unterberger 自己在 2018 年出版的一本關於數論的書籍《Pseudodifferential methods in number theory》。書籍介紹中就提到了「探索一種證明黎曼猜想的新方法」。
有趣的黎曼猜想
黎曼猜想是數學家黎曼在 1859 年向柏林科學院提交的一篇 8 頁短論文中提出的,這篇論文討論了素數分佈的問題。黎曼發現,素數分佈的規律就隱藏在某個函式的零點分佈中。這個函式就是黎曼 ζ 函式:
黎曼將該函式解析延拓至整個複平面,並指出:黎曼ζ函式的非平凡零點(是指 s 不為 - 2、-4、-6‧‧‧ 等點的值,這些都是平凡零點)的實數部分都是 1/2。也就是說,這些非平凡零點都分佈在複平面的 Re(z)=1/2 的直線上(即下圖中的虛線)。
要證偽黎曼猜想,只需要找到一個不在 Re(z)=1/2 這條直線上的非平凡零點即可,只不過目前還沒有發現這樣的零點。
黎曼猜想及推廣形式的成立是現有很多數學命題的前提。如果黎曼猜想及其推廣形式被證明,這些數學命題都將變為數學定理;反之,一旦黎曼猜想被證偽,將有 1000 多個數學命題成為黎曼猜想的「陪葬品」。
這項研究證明了黎曼猜想的什麼?
在這篇論文中,Andre Unterberger 對黎曼猜想涉及到的厄米特形式(hermitian form)的分析和算術部分進行了詳盡的比較,從而證明了該猜想。
該研究對黎曼猜想的證明基於對如下分佈的探究:
其中,
,
,r=1,2,...。
被稱作 Eisenstein 分佈,在某些情況下,
與分佈
相關聯的線性運算元
將 S(R)轉變為 S’(R)
該研究利用尤拉運算元
更具體地說是重新擴充套件了運算子的集合
,即
Unterberger 在 2018 年的一項研究 [1] 中,當β>2 且ε>0 時,對於在[0,β] 中的每個
R.H. 已經被證明等價於:
給定一個正整數 N,
如果 Q 無平方,且函式
在 [0, β] 中被支援,則 N = RQ 是一個可被所有小於 βQ 的素數整除的無平方整數,可得到以下方程:
現在,右側的厄米特形式適用於代數算術版本。實際上,將 half-line 支援的
中的函式傳遞到以下方程定義的線性情況下
上的函式:
與 [1] 中已獲得的證明結果相比,新研究在於充分利用了這種代數結構和測試函式 w 的支援假設。作者透過進一步的條件
來利用一切可能性約束 R,然後主厄米特形式(1.7) 本質上等於 Q^2 乘以「簡化」形式
。如果假設 w 在 [0, β] 中得到支援,對於某些 β,則可以使用主厄米特的簡單無條件估計形式,也就能夠對簡化形式實現非常好的估計。為了從中推匯出黎曼猜想,剩下要做的是為簡化形式提供一個類似於(1.5)的標準。
是民科?還是正經研究?有待同行評議
對於 André Unterberger 這篇證明黎曼猜想的論文,有知乎使用者吐槽稱,「有點像 mathgen(一種數學論文生成器)自動生成的。」
不過,更多的網友還是給予了肯定與期待。有位匿名使用者認為,「作者畢竟是法國數學家 & 1950 年菲爾茲獎得主 Laurent Schwartz 的博士生,法國數學家 & 1966 年菲爾茲獎得主 Alexander Grothendieck 的同門師弟,年逾 80,總歸非民科能碰瓷的吧。」
這位匿名使用者的觀點也得到了其他人的附議。「至少看上去有可能是對的,比某精細結構常數要靠譜得多。仍有很大可能存在缺陷,還是期待同行評議的結果。」有使用者這樣表示。
總之,對於這篇「不明覺厲」的文章,掛在了 arXiv 數論板塊(Number Theory)也在一定程度上說明了作者並非胡說臆測。如果有讀者大神研究這一證明,歡迎留言告訴我們結果。
參考連結:
https://zhuanlan.zhihu.com/p/45249464
https://www.jiqizhixin.com/articles/2019-01-12
https://www.genealogy.math.ndsu.nodak.edu/id.php?id=75970