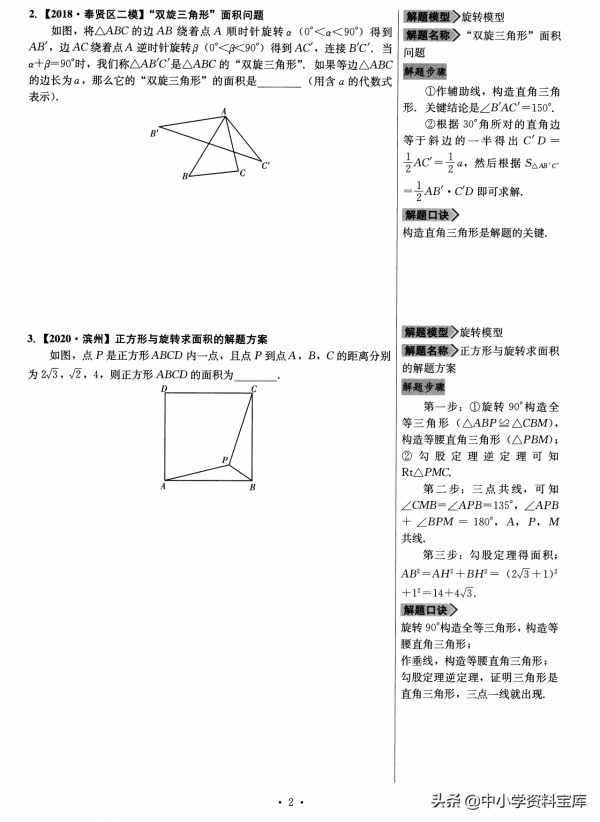
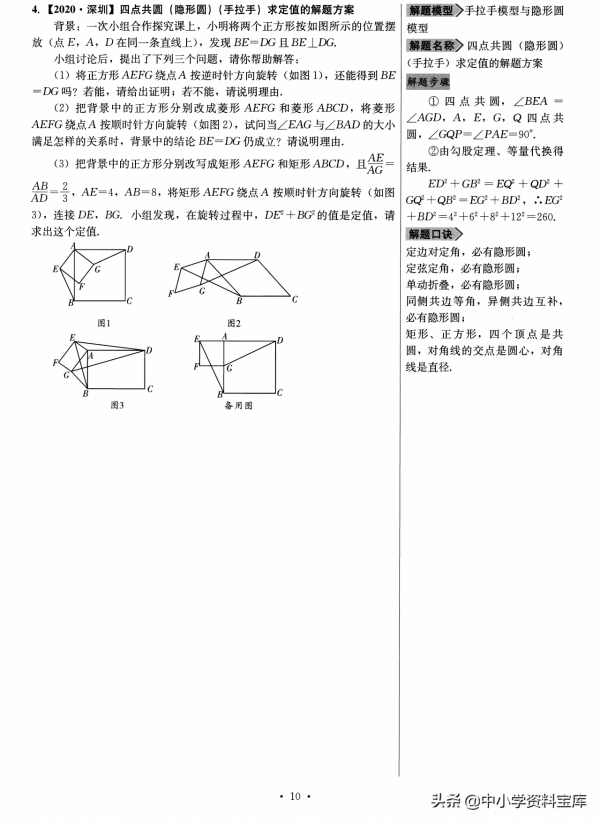
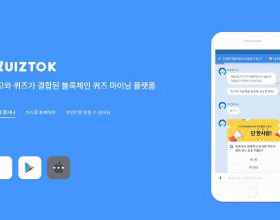
哪些情況可以考慮旋轉模型呢?
- 遇見中點要旋轉,
- 遇見等腰要旋轉(等腰三角形、等腰直角三角形),
- 遇見等邊要旋轉(等邊三角形),
- 遇見正方形要旋轉‘
- 等線段,共端點,必旋轉,必全等,有相似,要牢記。
三角形求面積,先作高;有定點,有定長,構造圓,相切角最大;全等,可知結果。
構造等邊三角形→旋轉→建立直角三角形→發現定值角→構造等邊三角形→畫圓→確定軌跡!
- 定邊對定角,必有隱形圓;
- 定弦定角,必有隱形圓
- 單動摺疊,必有隱形圓;
- 同側共邊等角,異側共邊互補,必有隱形圓;
- 矩形、正方形,四個頂點是共圓,對角線的交點是圓心,對角線是直徑
底邊是定值,垂直平分高最大
遇見平方等式,要用手拉手模型;
構造等腰直角三角形,構造全等三角形
等量代換是解題三要素
等腰圖形有旋轉,辨清共點旋轉邊,
關注三邊旋轉角,全等思考邊角邊
等線段,共端點,必旋轉,
必全等,有相似,要牢記
旋轉線段最大值,三點共線最合適。
- 定邊對定角,必有隱形圓
- 定弦定角,必有隱形圓;
- 單動摺疊,必有隱形圓;
- 同側共邊等角,異側共邊互補,必有隱形圓;
- 已知條件仔細看,對角互補是共圓;
- 四點共圓助相似,比值相等得整式;
- 設座標,靈活運用手拉手;
- 兩點之間的距離公式,勾股定理要想到,正確結果在眼前.