已知AD=BC，紅色角度數=？

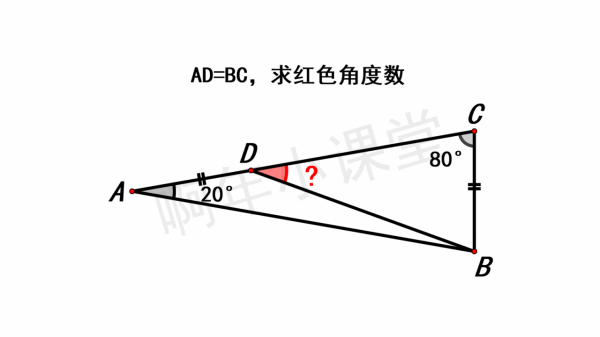
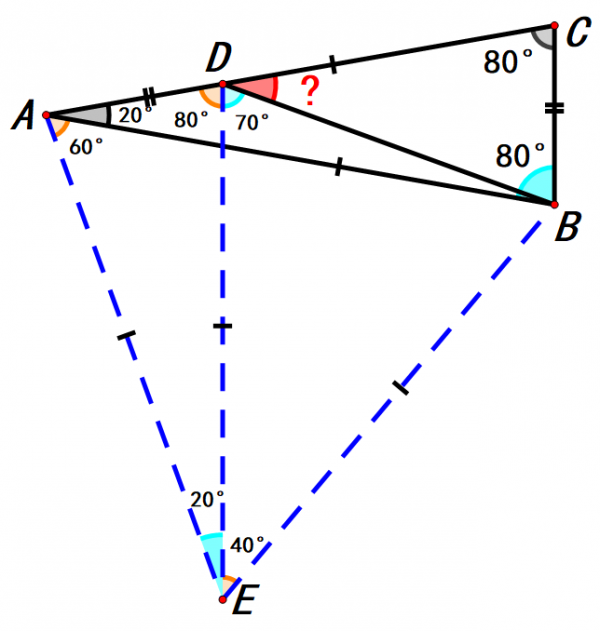
如圖所示，∠A=20°，∠C=80°，AD=BC，求∠BDC的度數。這題怎麼做呢？

根據題目條件，∠A=20°，∠C=80°，

可得∠ABC=80°（三角形的內角和為180°）。

∠C=∠ABC=80°，三角形ABC為等腰三角形，AB=AC。

就目前的資訊而言，我們很難求出∠BDC的度數，我們還是需要作輔助線的，但是如何構造呢？

現在有2組相等的線段，AD=BC，AB=AC，1組相等的角，∠C=∠ABC=80°，構造全等三角形是我們經常使用的方法，我們不妨嘗試去構造一下。

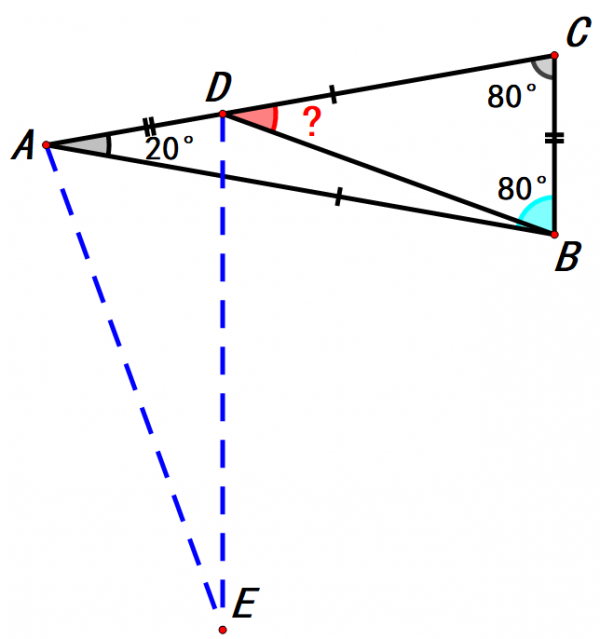
如圖，構造和三角形BCA全等的三角形ADE。

因為三角形ADE和三角形BCA全等，

所以∠AED=∠BAC=20°，∠DAE=∠CBA=∠ADE=∠BCA=80°，AE=DE=BA=CA，

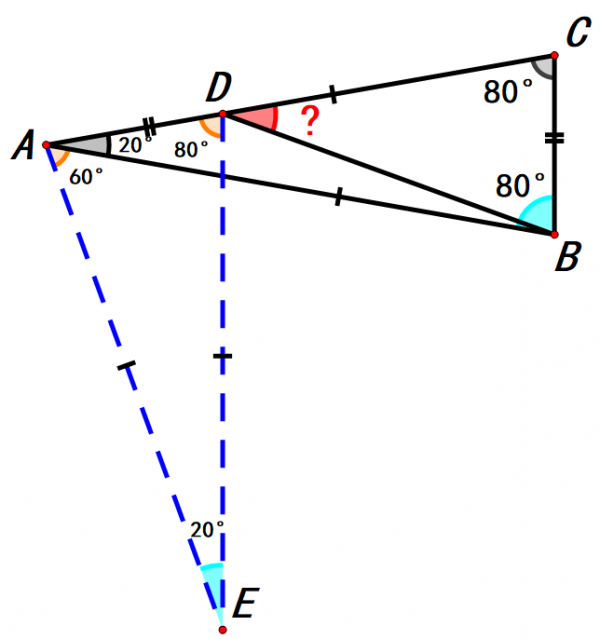
所以∠BAE=∠DAE-∠BAC=80°-20°=60°，

接著連線BE，

由AE=AB，∠BAE=60°，可得三角形ABE為等邊三角形，

所以BE=AE=DE，∠AEB=60°，

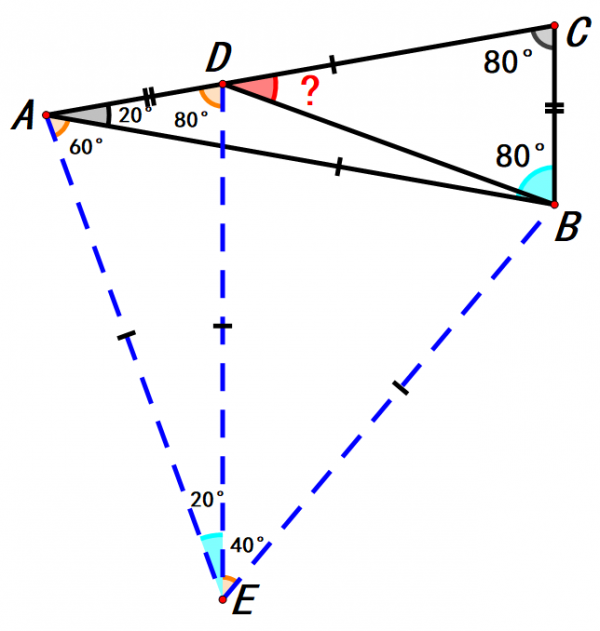
所以三角形BDE也是等腰三角形，

且∠BED=∠AEB-∠AED=60°-20°=40°，

所以∠EDB=∠EBD=70°，

而∠ADE=80°，

所以∠BDC=180°-∠EDB-∠ADE=180°-70°-80°=30°。

以上就是這道題的解法。

除此之外，你還有其他方法嗎？