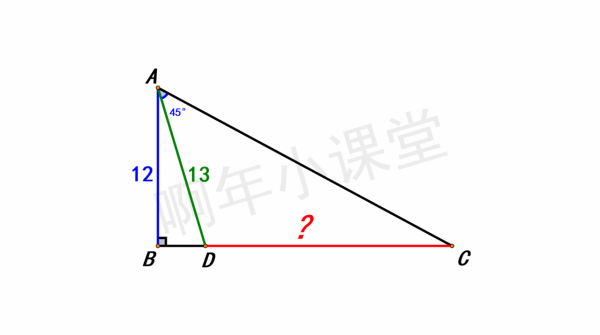
如圖,∠B=90°,∠CAD=45°,AB=12,AD=13,求CD的長。這題怎麼做呢?
首先根據題目條件∠B=90°,AB=12,AD=13,
可得BD=5(勾股定理:AB²+BD²=AD²)。
接下來怎麼做了?
根據現有的條件無法求出CD的長,我們需要作輔助線。
∠CAD=45°,45°是特殊角,它在直角三角形中非常有用,我們不妨去構造一個等腰直角三角形。
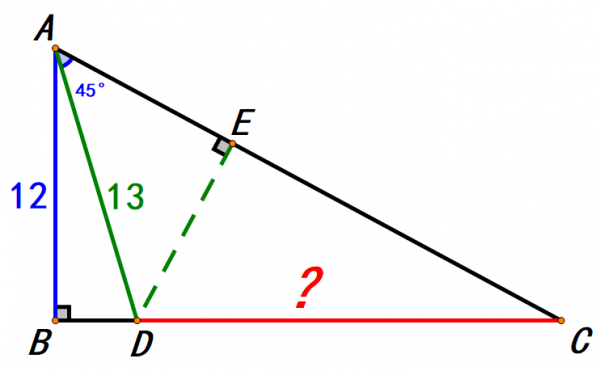
這裡的話不是過點D作AC的垂線,如下圖,雖然我們得到了一個等腰直角三角形ADE,但是對我們求CD的長並沒有太大的幫助。
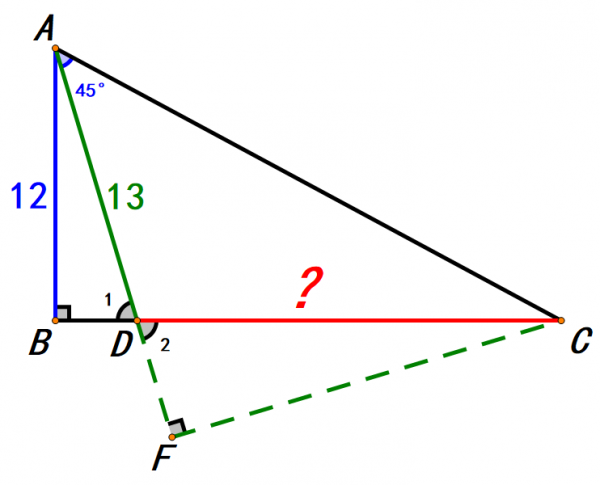
除此之外,我們還可以延長AD,過點C作AD延長線的垂線,
如上圖,AF⊥CF,三角形ACF為等腰直角三角形,
除此之外,三角形ABD和三角形CFD是相似的,為什麼呢?
如上圖,∠1和∠2是對頂角,∠1=∠2(對頂角相等),
∠B=∠F=90°,
所以三角形ABD和三角形CFD相似。
假設DF=x,則AF=13+x,
而三角形ACF為等腰直角三角形,所以CF=AF=13+x。
三角形ABD和三角形CFD相似,它們的對應邊成比例,
AB/BD=CF/DF,
12/5=(13+x)/x,
解得x=65/7,即DF=65/7。
求出了x的值,接下來可以透過勾股定理(DF²+CF²=CD²)求CD,也可以再用一次相似。
啊年選擇再用一次相似,這樣不用開方。
三角形ABD和三角形CFD相似,它們的對應邊成比例,
BD/AD=FD/CD,
5/13=(65/7)/CD,
解得CD=169/7。
以上就是這道題的解法,你還有其他方法嗎?歡迎在評論區留言~