如何獲得 "真正的 "隨機數?
檢查薛定諤的貓,並根據貓是活的還是死的生成0或1,這是生成隨機數的一個很好的方法。
英國統計學家蒂佩特在1927年發表了第一張隨機數表。這張表上的數字由從人口普查登記冊中“隨機”收集的數字組成。 儘管蒂佩特的隨機數表在當時被成功地用於驗證和發現新的分佈規律,但事實證明,書中給出的數字無法透過很多現代的隨機性測試。此外,各種研究都認為,我們(人類)很難生成真正的隨機數。但隨著物理學的發展,我們找到了比投擲骰子更有效地生成隨機數的方法。今天,我們離在智慧手機上建立量子隨機數生成器(QNRG)的光子探測器晶片不遠了——這將基於量子疊加原理。
我們為什麼需要隨機數?
數百億元的加密行業需要隨機數作為基本資源。從虛擬遊戲中的發牌等簡單應用到解決現代IT行業的加密問題,隨機數都是必不可少的。在統計分析和控制過程中,在蒙特卡洛型別的數值模擬中,在具有非確定性行為的人工智慧(AI)演算法中,或在遺傳演算法中模擬神經網路和進化,也經常需要隨機資料。
如何獲得 "真正的 "隨機數?
隨機數生成器可分為軟體生成器和硬體生成器。每一類中的一個子類會遇到網路安全的隨機數生成器。
偽隨機數生成器(PRNG)
獲得隨機數的一種有效方式是透過演算法生成隨機數,這些隨機數對許多應用來說已經足夠好。以這種方式獲得的 "隨機 "數被稱為偽隨機數,因為它們在知道初始引數和使用的演算法後很容易被複制,這意味著它們是確定的。可複製的隨機資料集在某些情況下可能是有益的,但如果別人能複製它們,它們在加密應用中一般是不安全的。
偽隨機數的缺點是,演算法是完全可預測的。此外,所有偽隨機數的序列最終都會重複。
偽隨機數生成器(PRNG)的演算法有很多。
- 一種是使用複雜運算結果四捨五入後的最後一位數字。
- 約翰-馮-諾伊曼的平方取中(middle-square)演算法被用來生成曼哈頓計劃中製造核彈所需的數值計算的數字——將數字平方並從中提取中間的四個數字。
目前標準和最廣泛使用的偽隨機數生成器是一種叫作Mersenne Twister)的演算法,它基於線性同餘生成器(linear congruential generator ),數字序列從除法的餘數中得到:
- x[n+1]=(a*x[n]+c)mod m
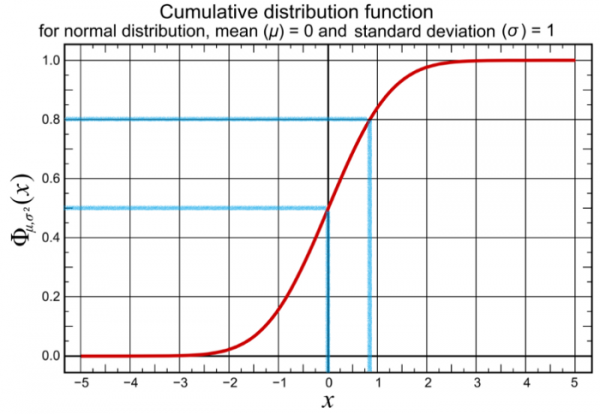
偽隨機數的抽樣通常是均勻分佈的。從均勻分佈的隨機資料中,人們可以使用反變換抽樣生成遵循任何其他分佈的隨機數——利用累積分佈函式的逆來調整隨機資料集。
- 均勻隨機數取樣發生器在[0,1]範圍內生成的數字0.5和0.7881分別對應正常隨機數發生器中生成的數字0和0.8——維基百科
加密安全的偽隨機數生成器(CSPRNG)除了透過統計隨機性測試外,還應該保持不可預測的狀態,即使攻擊者可以使用它們的部分初始狀態或執行狀態。大多數偽隨機數生成器不適合作為CSPRNG使用。
真隨機數生成器(TRNG),混沌的經典系統
- 熔岩燈在產生隨機數方面比電腦要好
對於電子安全和密碼學來說,不可預測的不可複製的數字是至關重要的,所以PRNG的使用並不 "足夠隨機"。與偽隨機數生成器相比,真隨機數生成器(TRNG)更慢、更復雜,因為它們必須使用外部裝置。
真隨機數與其說是生成的,不如說是取樣的。
經典真隨機數生成器是由高熵的混沌宏觀物理系統產生的,測量系統的變化。經典真隨機數可以由大氣噪聲、宇宙輻射、開放空間中溫度計給出的最後數字等產生。使用經典系統生成真隨機數集並不那麼困難,而且它比偽隨機數集更安全,因為它不是由任何特定的演算法生成的。
量子隨機性,真正的量子隨機數生成器(QRNG)
最好是使用量子力學系統生成隨機數。從量子力學的入門課程中,從斯特恩-格拉赫實驗中可以知道,量子系統中的一些可測量的量具有內在的不可預測性。為了從量子源產生資料,可以使用非常簡單的高熵的量子力學系統。
基於我們今天所知道的--量子世界的底層特徵是不可預測的。量子隨機性是自然界的根本。
在實踐中,隨機性的量子源與經典的噪聲或確定性因素混合在一起,導致產生的隨機序列出現偏差。來自經典源的影響可以在過程中或在後期處理中減少。儘管理論上是完全隨機的,但量子協議的實施總是隻在一定程度上是安全的,安全性的提高通常是以整體效率為代價的。測試隨機性仍然是該過程的一個重要部分,即使對於量子隨機數生成器也是如此。
隨機性的數學定義
儘管隨著機率論和統計學基礎的建立,隨機性的概念已經被討論了至少100年,但隨機性的數學定義並不完整。蘇聯數學家柯爾莫戈洛夫對數學機率論和演算法資訊理論的建立作出了重要貢獻,對數學中的隨機性理論做出了巨大的貢獻。他在20世紀60年代對隨機性的定義是基於計算複雜度的有限字串。
非正式定義:如果複製字串的最短方法是列印字串,則將其視為柯爾莫戈洛夫隨機字串。當且僅當一串位元短於任何能複製該串的計算機程式時,它就是隨機的。隨機字串是那些不能被壓縮的字串。最短描述的長度取決於程式語言的選擇,但這種效果是有限的。
根據柯爾莫戈洛夫的定義,π不是隨機的,因為存在有限的程式可以複製π的任何一位。然而,柯爾莫戈洛夫的隨機性定義,也被稱為演算法隨機性,是不完整的。他本人對自己的定義並不滿意,他望能更好地將隨機性的不可預測性形式化。
我們總是可以構造一個確定性生成器,它將生成一個透過所有(有限)數量的隨機測試的序列。
一些科學家認為,對隨機性的嚴格定義可能超出了數學的範圍,因為數學工具可能不足以形成一個框架來定義隨機性。問題仍然存在——如果隨機性是一個物理概念而不是一個數學概念,它能在數學中正式表述出來嗎?