世間萬物的複雜性,很多就是從一些簡單的規則開始,透過系統自發的相互作用產生,這就是神奇的自組織。自組織現在被發現出現在自然科學乃至社會科學的諸多領域,本文主要介紹數學上最早的概念模型:阿貝爾沙堆模型。
撰文 | Jordan Ellenberg(威斯康星大學麥迪遜分校數學教授)
編譯 | 許釗箐
你聽說過多米諾骨牌理論(Domino theory)嗎?這是冷戰時期美國為遏制共產主義提出的地緣政治理論,指社會主義國家會輻射影響周邊國家進行社會主義變革。此理論極大地影響了美國二十世紀中期的外交政策,被用來為其霸權主義行為正名。但拋開政治理論,在自然界確實也有類似的多米諾骨牌行為,從物理學的角度上講,它應該被稱為 “沙堆理論(sandpile theory)”。
現實世界的政權轉變往往不是有條不紊的發生,而是在突然間的協調配合下發生的,比如阿拉伯之春以及東歐劇變(最終蘇聯解體)。這些歷史事件中,平靜的時期裡暗藏危機,然後在某一刻陡然倒塌。就像沙堆一樣,假如你在一個沙堆上頂部再放一些沙礫,沙堆可能在短時間內沒有明顯變化。但是,頃刻間,類似於一場雪崩,頂部的沙礫會以不規則的方式突然衝下,並且在過程中很可能引發小的次級流沙。
這個比喻不一定會給我們帶來什麼。畢竟,真實的沙子很難去分析,就像現實世界的政治一樣。但奇蹟也在這裡,物理學家巴克(Per Bak),湯超(Chao Tang)和維森菲爾德(Kurt Wiesenfeld)在1987年提出了一種由沙堆的抽象而來的 “阿貝爾沙堆模型(Abelian sandpile model)”。這種模型在保持足夠簡單以便於應用數學來研究的同時,似乎又可以刻畫真實沙堆的一些有趣但無序的特點,並且適用於其他一些源自生物學、物理學以及社會科學的複雜系統[1]。
阿貝尓沙堆模型
它的過程是這樣的:我們可以想象一個無窮網格,在每一個網格上都有一小堆沙子,並在每一個格子內用數字表示沙礫的數目。
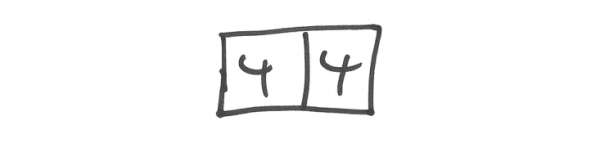
但在垂直方向沙堆的高度是有一定限制的。所以這裡假設每當網格中沙礫數目到達四,則四粒沙礫會向周邊四個格子流散。所以如果初始是兩個網格中有四粒沙礫:
則沙堆流散之後左側的網格變成了:
此時右側網格已經超過四粒的沙堆,那麼它會繼續朝周邊的四個網格各流散一粒沙礫:
現在因為所有位置的沙礫數目都不超過四,每個網格點都處在穩定的狀態,所以沙堆流散的過程就停止了。
以上的分析過程中,我們先進行的是原本兩個網格中左側的流散,其次是右側的。我們如何知道哪個網格應該先向四周流散呢?好訊息是,選擇的順序並不重要。因為我們可以由穩定狀態網格的對稱性得出,這種“阿貝爾沙堆”的最終狀態並不取決於我們選擇模擬流沙網格的順序。這也是其取名為阿貝爾的原因,意味著我們選擇的先後順序不影響最後的結果。[譯者注:數學命名中的阿貝爾通常是為了紀念挪威數學家尼爾斯·阿貝爾(Niels Henrik Abel,1802-1829)。他開啟了許多領域的研究,並以證明五次方程的根式通解不存在以及橢圓函式的研究聞名。儘管他數學成就極高,但其生活遇到了很多困難,最後因肺結核不滿27歲逝世。]
比如說,加法這種運算是阿貝爾的,我們指加法中元素是可以交換的:先加2再加3等價於先加3再加2。但是大多數的運算或操作都不是阿貝爾的。比如說先解鎖汽車,再拉開車門,那麼車門就打開了;但是先拉車門,再解鎖汽車,得到結果完全不同——車門還是關閉的。所以沙堆的阿貝爾性質可以算是一個驚喜。
那麼你可能會問,如果我們在一個網格上放很多很多沙礫,比如說一百萬粒,會發生什麼?當沙礫向四周不斷流散,最後穩定下來時會是什麼樣子?你可能會想象最後會是一個巨大平整的沙堆,其中接近中心的一個很大的區域會有很多包含三個沙礫的網格。
但並不是這樣。下面這幅圖展現了最終穩定後的網格情況:
百萬沙粒:中心點上堆積大約大量的沙礫 (準確地說是2的20次方)來模擬一個阿貝爾沙堆。(顏色表示堆高。藍色表示沒有沙子。紫色表示一粒,黃色表示兩粒,褐紅色表示三粒。)丨圖片來源:Wes Pegden
好吧,會不會是一百萬不足以使得沙堆數量是光滑變化的?如果我們用十億粒沙礫呢,會得到一個平坦的大的沙堆嗎?最終的影象是這樣的:
十億粒沙礫模擬圖丨圖片來源:Wes Pegden
我們期待的平坦情況沒有出現。相反,那些奇異的分形圖樣持續存在。在接近中心的地方,複雜的圖案就像是一個圓頂,其內部還鑲嵌著很多格子,看起來是某種幾何圖案但又像是隨機的;在沙堆的邊界,則是眾多一致的三角形,以規則的模式緊密連線。
這些圖片是由卡內基梅隆大學的數學教授Wes Pegden及合作者康奈爾大學的Lionel Levine和Charlie Smart在沙堆的前沿研究中繪製的[2]。在Pegden教授的網站上,甚至可以看到十億粒沙堆的互動式的圖片,我們可以將其放大或者移動到任何位置再放大,比如直接觀察沙堆的中心:
十億粒沙堆的中心影象丨圖片來源:Wes Pegden
或者看到外緣尖銳怪異的細節:
十億粒沙堆的邊緣影象丨圖片來源:Wes Pegden
如果仔細觀察,你還可以觀察到更精細的區域性結構。像很多數學文章一樣,我們在這裡給感興趣的讀者一個家庭作業:沙堆穩定之後,請說明兩個鄰近網格為什麼不可能同時為空?(有答案!)事實上,一些實驗表明,我們可能有更強的結論:空的網格不僅不會相鄰,它們甚至傾向於不接近彼此,就像帶相同電荷的粒子,它們會相互排斥。
複雜中所蘊含的簡單規律
在你真的去拿顯微鏡觀察沙堆之前,我不得不提醒你,真正的沙堆是不會產生這種自發性的結構的[3]。這裡的阿貝爾沙堆模型甚至不具有模擬真實物理材料的性質。相反,我們看到的所有複雜性都來自於一個抽象、簡單的確定性演算法,甚至只用五行程式碼就可以寫下。這不禁讓人想到約翰·康威(John Conway)的《生命遊戲》(Conway's Game of Life,https://playgameoflife.com/ )。這個遊戲也是從非常簡單的規則中產生了豐富的複雜性。就像《生命遊戲》一樣,阿貝爾沙堆也是一個元胞自動機(cellular automaton):它是一個微型的宇宙,其中的執行規律可以被計算機可接受的離散語言全然描述。在沙堆中,每個網格都具有從0到4中的一個數字,透過一個簡單的規則決定相鄰網格的值。而在《生命遊戲》中,網格的狀態更為簡單,每個狀態非生(值為1)即死(值為0)。
但是兩者還是有區別的:《生命遊戲》作為一種典型的元胞自動機,複雜的行為可以出現,但更傾向於簡單的模式[4];但是對於沙堆模型,我們似乎不需要特別設定初始條件,它就會自動趨向複雜的模式。
實際上,沙堆中複雜行為的出現取決於一個所謂的臨界閾值,在這個值附近,往往會出現複雜的行為。我們對於自然界中的臨界閾值這一概念是很熟悉的:水在較高溫度下是一種無序的液體,但是當溫度下降到達某個臨界值,水就會發生巨大的轉變——結晶成冰。而對於沙堆來說,它的密度就類似於水的溫度。(這裡的密度是指平均每個網格中有多少的沙礫。)如果有太多的沙礫,沙堆就會不穩定,“雪崩”隨之發生;如果沙礫太少,沙堆則會很快穩定下來。那麼多少算是我們說的太多呢?事實上,這個答案出乎意料的簡單。巨大變化和微小變化的分界線是:平均每個網格里2.125粒沙礫。
值得注意的是,在網格有限,並假設當沙礫到達邊緣格子時再流散就會消失的情況下,平均每個網格的沙礫數會是2.125。在一開始,所有的網格都是空的,我們一粒一粒地將沙礫放至中心的那個網格。一段時間後,沙堆開始向四周流散,會慢慢形成類似於我們之前展示過的Pegden教授生成的影象(這個影象是假設網格在所有方向都有無限多個。)我們扔下一粒沙,待沙堆穩定後,就再扔下一粒,這樣沙礫會越來越多。但如果沙礫到達邊緣,流散出去的沙礫就消失了。此後沙堆會接近一個平衡:沙礫在邊界掉落的速率等於我們增加沙礫的速率,密度會在某個臨界值穩定下來。當然,系統會有區域性波動,隨著時間推移,密度低的地方和密度高的地方會有一定的交替變化,但對於整體,平均每個網格沙礫數會在2.125粒左右。
如果一開始我們儘可能地將每個網格佈滿沙礫,即每個網格放置3粒,那會發生什麼呢?這種初始佈局是穩定的,但它是很脆弱的穩定。我們在任意一個網格放置一粒沙礫,之後一場巨大的“雪崩”就開始了,直到密度下降到2.125它才會停止。
那麼,當沙礫密度到達臨界值時會發生什麼?這時的沙堆會處在最有趣的狀態。向四周流散的過程一直在發生,但卻不是持續的大範圍混亂狀態;相反,流散會出現類似於海浪一波接一波,不時也會發生罕見的橫跨所有網格的雪崩災難。而流散活動在閾值密度下的分佈似乎遵從冪律,流散活動的頻率和它的規模成反比。其中也有持續的流散活動,但它們是有某種結構和規律的。不僅如此,為了展示其複雜的行為,沙堆不需要做精細的調整,它自己具備調整的能力。不論系統從哪裡開始,只要新的沙礫以常數速率增加,系統都會通向臨界閾值狀態。
眼見為實。美國國家標準技術研究所(NIST)的R.M. Dimeo就製作了一個系列沙堆處於臨界狀態的無聊電影。
沙堆中加入一粒沙子後的變化,顏色代表該處流散的次數,每次流散都會“更熱”。影片來源:R. M. Dimeo【請前往“返樸”公眾號觀看影片】
對我來說,這個過程看起來就像是有生命力的,而不是一個巧合。思考豐富的生命結構是如何從簡單系統中湧現出來的,它們會自動尋找臨界閾值,使用自組織臨界性的概念是一種流行的方式。一些生物學家認為自組織臨界性是複雜生物行為的潛在統一理論。這一理論支配著一群鳥兒同步飛行的模式,就像遺傳資訊支配鳥兒個體的發展一樣[5]。理論生物學家斯圖亞特·考夫曼(Stuart Kauffman)寫道,“生命系統存在於臨近混亂邊緣的一個穩固的狀態,是自然選擇實現並維持了這種平衡狀態。” 就像是我們討論的沙堆。它當然不是一個生命,但它卻生機勃勃,不是嗎?
沙堆是第一個,也是被研究的最多的自組織臨界性的例子。此外還有很多其他的例子。(在Pegden教授的網站上還有一些。) 但是,我們並不知道沙堆的散落規則到底是什麼,為什麼它使得系統不可避免地朝著複雜的臨界狀態發展;也不清楚哪些元胞自動機可能表現出這種自組織臨界性。
一些深刻的理解可能會從沙堆理論和其他數學理論的驚人聯絡中產生。對於我這樣的幾何學家來說,沙堆理論與最近新興的熱帶幾何學理論(tropical geometry)有關,該領域的目標是用類似的離散幾何現象來模擬連續的幾何現象。[譯者注:熱帶幾何學理論是首先由巴西數學家及計算機科學家伊姆雷·西蒙(Imre Simon)於1980年代發展,“熱帶”一詞源於部分法國數學家對於巴西的刻板印象。熱帶幾何可以看成是分片線性化的代數幾何,在計數代數幾何中有重要的應用。]
對於機率學家來說,沙堆與所謂的生成樹密切相關。生成樹(在方形網格上)是一個分支路徑,它接觸網格上的每個點,但不會形成閉合的迴路。無論這些理解是來自於哪裡,沙堆理論提醒我們,數學中非常有趣的現象,就像物理學很多有趣的現象,經常出現在相變之中。就是在這裡,我們處於兩個不同的數學理論之間,既擁有它們的特徵,又可以跨越邊界傳遞資訊和問題。當然通常來說,問題總是比答案多。
參考資料
[1] Bak, P., Tang, C., & Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters 59, 381-384 (1987).
[2] Levine, L., Pegden, W., & Smart, C.K. Apollonian structure in the Abelian sandpile. preprint arXiv.:1208.4839 (2014).
[3] Mehta, A. & Barker, G.C. Disorder, memory and avalanches in sandpiles. Europhysics Letters 27, 501-506 (1994).
[4] Aron, J. First replicating creature spawned in life simulator. New Scientist 2765, 6-7 (2010).
[5] Mora, T. & Bialek, W. Are biological systems at criticality? Journal of Statistical Physics 144, 268-302 (2011).
本文譯自Nautilus “Dominoes” 2015年4月刊
https://nautil.us/issue/107/the-edge/the-math-of-the-amazing-sandpile