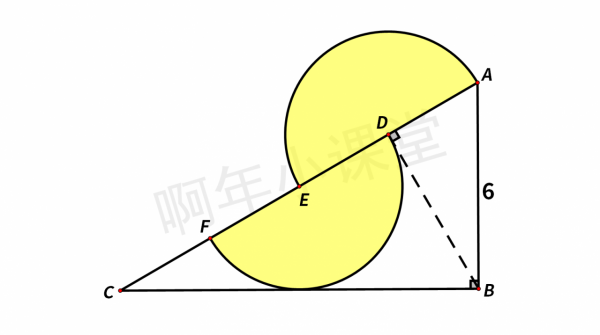
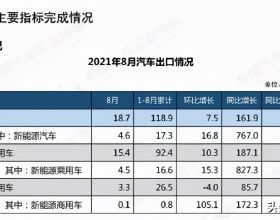
如圖,∠ABC=∠ADB=90°,D、E為半圓圓心,半圓E和BC相切,AB=6,求陰影部分面積。這道題怎麼做呢?
從圖中可以看到,陰影部分是由2個半徑相同的半圓組成。
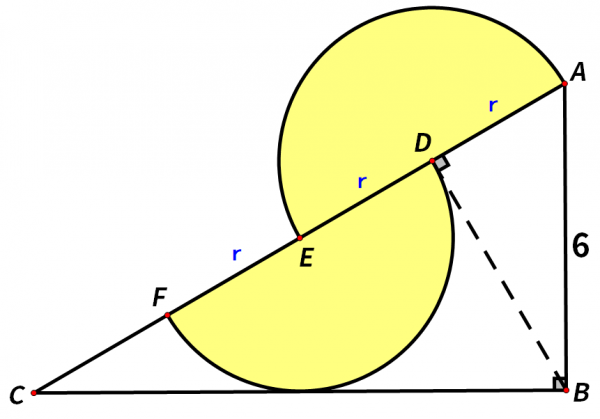
我們要求陰影部分的面積,就需要知道半圓的半徑,我們不妨假設半圓的半徑為r,AD=DE=EF=r。
接下來我們只要構造出1個和r有關的方程,就能求出r。
在三角形ADB和三角形ABC中,
∠ADB=∠ABC=90°,
∠DAB=∠BAC(公共角),
所以三角形ADB和三角形ABC相似。
三角形ADB和三角形ABC相似,它們的對應邊成比例,
AD/AB=AB/AC,
而AD=r,AB=6,AC=3r+CF,
CF是未知的,我們還需要求出CF,如何操作呢?
我們回想一下,題目中還有哪個條件沒有使用?
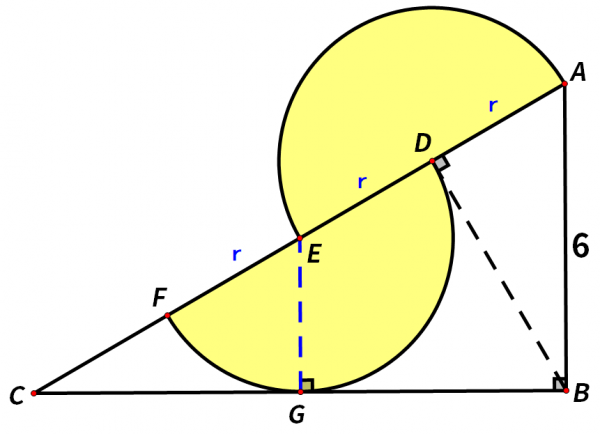
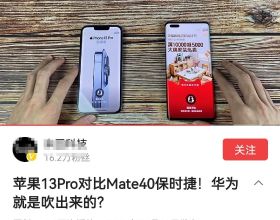
半圓E和BC相切,我們不妨將圓心E和切點連線起來。
如圖,三角形EGC也是直角三角形,且EG=r=AD。
也就是說在三角形EGC和三角形ADB中,
已經有了一組對角相等,∠EGC=∠ADB=90°,
一組對邊相等,EG=AD=r。
如果可以再找到一組對角相等,就能證明三角形EGC和三角形ADB全等。
三角形EGC是直角三角形,∠C+∠CEG=90°,
三角形ABC是直角三角形,∠C+∠BAD=90°,
等量代換可得,∠CEG=∠BAD。
根據角邊角證全等,就得到了三角形EGC和三角形ADB全等。
三角形EGC和三角形ADB全等,EC=AB=6。
那麼AC=AE+EC=2r+6。
三角形ADB和三角形ABC相似,它們的對應邊成比例,
AD/AB=AB/AC,就是r/6=6/2r+6,解得r=3。
陰影部分的面積=9Π。
以上就是這道題的解法,你還有其他方法嗎?歡迎在評論區留言~