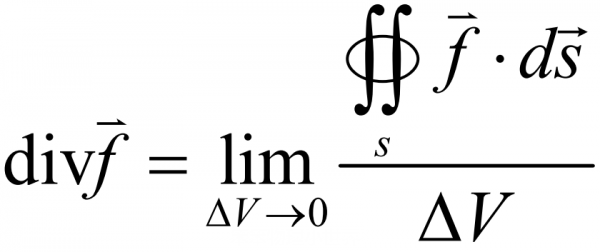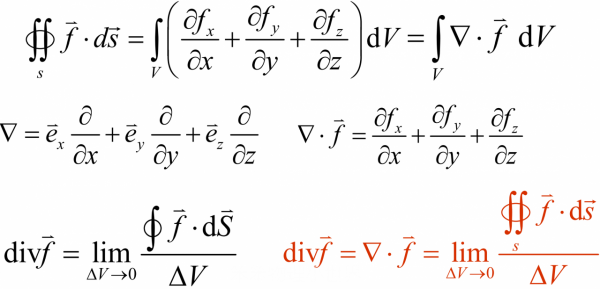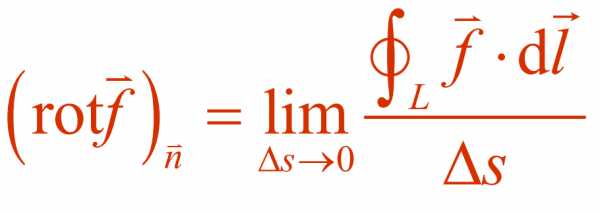向量分析(01)
麻煩各位喜歡的小夥伴點一下關注哦
假如你熱愛物理,那你一定不會對麥克斯韋感到陌生,他寫出的方程組揭示出電磁相互作用的完美統一,以麥克斯韋方程組為核心的電磁理論,是經典物理學最引以自豪的成就之一。
那麼接下來我們就將透過對於電動力學的探索來進入電和磁這個奇妙的世界。
笨笨要在這裡先提醒一下各位閱讀的小夥伴,作為電動力學專題的開篇內容,向量分析顯然是很重要但又很枯燥的,但是它將是我們揭示電磁世界的奧秘時所能用到的最棒的工具之一。
在本節內容中將不再對向量的基本概念進行贅述。
向量的基本運算
The basic operation of a vector
首先我們先簡單的看一下向量的運算規則。我們先給出一個三位正交座標系中的三個向量A、B、C:
我們可以簡單的得到向量點乘與叉乘的運算公式:
A·B=B·A=ABcosθ
AxB=-BxA;|AxB|=ABsinθ
此外,還有兩個常用恆等式:
(1)A·(BxC)=B·(CxA)=C·(AxB)
(2)Ax(BxC)=B(A·C)-C(A·B)
對於(1)式,我們可以看到(BxC)所得到的向量,其的數值大小即代表以B、C為邊的平行四邊形的面積,其方向垂直與BC面,當這個向量與A點乘,Acosθ顯然為該立方體BC面上的高,最後所得到的標量大小即為該立方體體積。對於B·(CxA)與C·(AxB),我們也可用相同的思路證明其結果為該立方體體積,顯然(1)式成立。
對於(2)式,我們進行簡單的分析幫助記憶,(BxC)為垂直於BC面的向量,由於A也垂直於BC面,顯然該向量與A所構成的平面與BC面垂直,當A與其叉乘,那麼所得向量必然處於BC面,我們就可以用B、C兩個向量將其表示出來。對於該式的證明過程如下:
梯度、散度、旋度
Gradient, Divergence, Rotation
在介紹梯度、散度、旋度之前,我們先引入一個小標誌——∇,∇讀作“del”或“nabla”,它是對場量作空間一階偏導數運算的算符。
∇·∇=∇²,∇²是二階齊次偏導數運算的標量算符,即拉普拉斯算符。
在直角座標系中:
梯度:
那我們接下來來看看什麼是梯度?梯度的本意是個向量,既然是向量那就是有方向的。一個函式在某一點的梯度所具有的方向便是該函式在該點變化率最大的方向,而變化率的大小恰好也是梯度的模(梯度的數值大小)。
我們假設有一標量場 φ(x),則梯度記作:
gradφ=(∂φ/∂l) ·l
假如在三維空間中我們就有:
很顯然,我們就有gradφ=∇φ
散度:
那麼什麼又是散度呢?散度簡單講就是指空間各點中向量場發散的程度。由此我們可以得出,散度只有大小沒有方向,若散度的取值為正則發散;若取值為負則匯聚。
舉個例子,我們在空間中放入一個正點電荷,很顯然,它所產生的電場是以它為源點向四周發散的,那麼電場某一點的散度就表示該點發散的程度。假如我們畫出電場線來表示電場,就不難發現,電場線越密集的地方就是散度越大的地方。在物理上,散度表示了場的有源性。
下面我們給出散度的定義:
當等式右邊的ΔV不取極限時,分式表示的是向量場f(x)在ΔV中單位體積的平均通量或平均發散量;當ΔV取極限時,便向一點收縮,若極限值存在,則稱其為該點的散度,利用高斯定理,我們便能得到:
注意,當我們用nabla算符表示時,梯度和散度是不同的。梯度是∇f(x),是向量;散度是∇·f(x),為標量。
旋度:
最後,我們來看看旋度是什麼。設想將閉合曲線縮小到其內某一點附近,那麼以閉合曲線L為界的面積也將逐漸減小。一般說來,這兩者的比值有一極限值,即記作單位面積平均環流的極限:
它與閉合曲線的形狀無關,但顯然依賴於以閉合曲線為界的面積法線方向且通常L的正方向與規定要構成右手螺旋法則,顯然,旋度是一個向量,是存在方向的。為此定義:
旋度的重要性在於,可用透過研究表徵向量在某點附近各方向上環流強弱的程度,進而得到其單位面積平均環流的極限的大小程度。當rot f(x)=0時,向量場為無旋場。
舉個例子,一根通電直導線所產生的磁場便是有旋場,我們可以來計算該磁場的旋度。而點電荷所產生的電場便是一個無旋場。
至此,梯度、散度、旋度都已經簡單地介紹完成。也許有些小夥伴還有點迷糊,不過只要記住梯度的方向是變化最快的方向,梯度的大小是最大的變化率;散度我們靠點電荷來理解;旋度我們則靠通電直導線產生的磁場來理解。這樣我們便會對電場與磁場有一個初步的熟悉,也會為我們之後進一步地深入探究鋪平道路。
Next issue
下一期的電動力學專題我們還是得繼續向量分析的學習,我們將會掌握有關nabla算符的一些運算律以及常用公式,當然,這還是很枯燥的內容,但它會對我們之後的學習非常有用。
各位對電磁世界好奇的小夥伴,我們下期專題見啦,喜歡的話記得點一下關注呀!
如果想要更好的閱讀體驗可以關注微信公眾號:笨笨物理小世界。公眾號裡的排版會更好一些,謝謝大家啦,下期再見!
編 輯|笨笨
校 對|笨笨
審 核|笨笨