瑞士數學家尤拉除了發現複數的尤拉公式以外,還有一個尤拉公式是有關多面體的。
大多數立體圖形是由多邊形區域組成的。 這些區域是面、邊和頂點。 具有面、邊和頂點的實體幾何形狀稱為多面體。
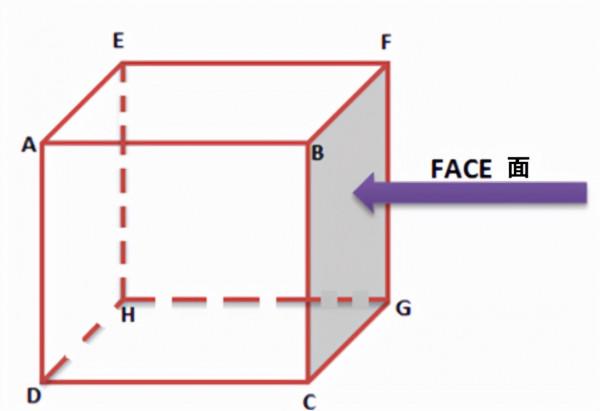
- 立方體和長方體有六個面。
- 錐體有平面和曲面。
- 圓柱體有兩個平面和一個曲面。
- 球體有一個曲面。
- 立方體和長方體有12條稜。
- 錐有一條邊。
- 圓柱體有兩條邊。
- 球體沒有邊。
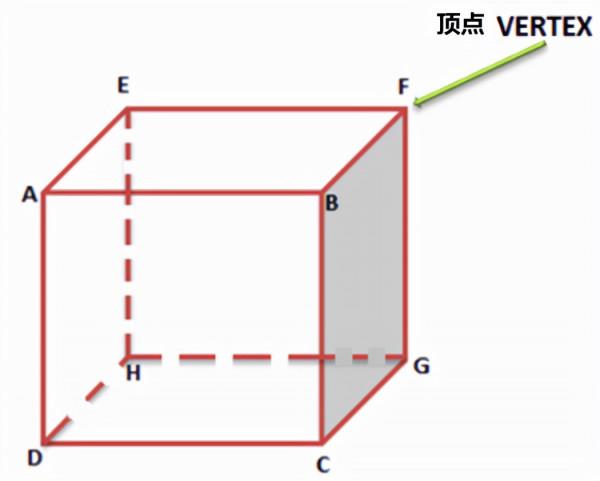
- 立方體和長方體有8個頂點。
- 錐有一個頂點。
- 圓柱體沒有頂點。
- 球體沒有頂點(表面是曲線)。
多面體的種類
凸面體:如果多面體的表面(由它的面、邊和頂點組成)不與自身相交,並且連線多面體任意兩點的線段位於其內部部分或表面內,則該多面體為凸多面體。
凹面體:非凸多面體稱為凹多面體。
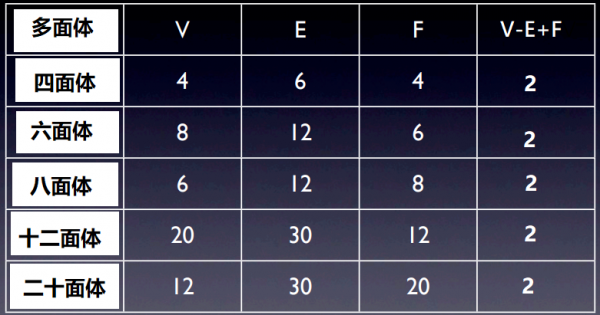
尤拉公式: 對於任何凸多面體,頂點(V)與邊(E)以及面(F)的關係有如下等式:
V-E+F=2
這個公式要結合英語的三個單詞Vertex, Edge和Face首字母來記憶。
尤拉是在寫給哥德巴赫(就是著名1+1=2的那個數學家)一封信中公佈的這個公式,隨後他給了一個證明,但這個證明是錯誤的,但其它的數學家證明了這個公式,目前已知有17種證明,其中一種證明方法採用球面幾何。
這個簡單而美麗的公式導致了19、20世紀對拓撲,代數拓撲學和曲面理論的深入研究。
此外在圖論、計算幾何、 以及數學的其他部分也有應用。