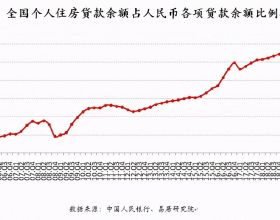
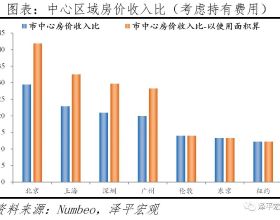
摘要:爆轟具有較高的燃燒效率,當應用於推進系統時,有較寬廣的前景,故引起國內外學者廣泛的關注。與爆轟有關的兩個重要現象是——爆轟的生成和傳播。爆轟的生成分為直接起爆和間接起爆。直接起爆需要極高的能量,因此間接起爆一直是研究的熱點,其中爆燃轉爆轟則是關注的重點。然而,經過幾十年的實驗、理論和數值研究,DDT的機理已被理解,但是準確的預測還無法實現,這其中最核心的因素是湍流燃燒。對於爆轟波的傳播,特別是高活化能的可燃氣體,其波陣面呈強不穩定結構,存在湍流燃燒,波後出現的未燃氣團的燃燒也屬於湍流燃燒,這使得爆轟波的精確控制也存在較大的困難,但是爆轟波傳播的平均速度仍然可以用CJ速度來預測。本文對DDT和爆轟波結構中的湍流燃燒的研究現狀進行了分析和評述,並對未來的研究進行了展望。
關鍵詞: 湍流燃燒 爆炸力學 爆轟 爆轟傳播 爆轟生成
爆轟是由激波誘導的、以穩定方式傳播的燃燒。由於該燃燒的化學反應比較激烈,故具有極高的火焰傳播速度,其產物也具有極高的溫度和壓力。因此,爆轟是一種具有更高熱效率的燃燒方式,將其應用到推進系統,具有廣泛的應用前景,比如脈衝爆轟發動機、駐定爆轟發動機和旋轉爆轟發動機等。另一方面,爆轟波後的高溫高壓環境具有較強的破壞能力,會引發各種工業災害,比如煤礦瓦斯爆炸、各種粉塵爆炸等事故。因此,為了對爆轟有更好的控制,需要對爆轟波的特性有更深入的瞭解[1,2]。
與爆轟密切相關的兩個現象是爆轟波的生成和傳播。爆轟波的生成主要有兩類———直接起爆和間接起爆[3]。直接起爆需要較高的能量[4],因此,普通工業生產和生活中遇到更多的是間接起爆。其中由弱點火先形成層流燃燒,再逐漸發展成爆轟的方式稱為爆燃轉爆轟(DDT),這種方式需要較小的點火能量,因而受到廣泛的關注和研究。在DDT過程中,層流燃燒依靠分子輸運來維持火焰面的傳播,是以亞聲速傳播的膨脹波,屬於輸運預混火焰;而爆轟依靠激波誘導來實現火焰面的傳播,是以超聲速傳播的激波,屬於對流預混火焰,這是兩種不同的火焰傳播模式,要實現它們之間的轉換,湍流起到至關重要的作用[5]。目前為止,在一定的初始條件和邊界條件下,很難精確地預測爆燃轉爆轟是否能發生以及何時何地發生。定性上來說,相關的機理已經研究得較透徹,但仍無法精確預測的主要難點在於其中的湍流燃燒。與爆轟密切相關的另一個現象是爆轟波的傳播,對於活化能較大的高度不穩定可燃氣體,激波陣面脈動很大,波系之間的作用使反應區呈現湍流狀態,湍流脈動會影響波陣面處的燃燒,進而影響爆轟波的傳播[3]。此外,由於反應誘導區較寬,可燃物在波陣面不能完全燃燒,會在其下游形成燃燒產物包圍的未燃氣團,該未燃氣團的消耗需藉助於湍流擴散來完成燃燒,釋放的能量有可能會影響爆轟波陣面[6]。
氣相爆轟波的傳播速度在馬赫數5左右,具有高馬赫數、高雷諾數和高溫高壓的特性,其中涉及到燃燒、高強度湍流、波系(包括激波、膨脹波等)之間的相互作用。在理論研究方面,採用Navier-Stokes方程來描述爆轟波的結構及其傳播特性,這是一組偏微分方程,在高雷諾數下方程會失穩。此外,方程還具有奇異性(超聲速流中的聲速點),導致流場出現壅塞,這些因素使得理論求解上述偏微分方程組沒有可能,只得藉助於實驗測試和數值模擬。隨著實驗測試技術的發展,很多光學測試手段已經較好地應用在了爆轟波的研究中,比如紋影、陰影、全息干涉、鐳射誘導熒光等,這些測試得到的影象反映的是光強和位相的資訊,經過適當的轉換,就可得到流場的引數分佈。然而,實驗得到的引數有限,且多為定性分析,難以進行定量研究。由於氣相爆轟波的三個特點,數值模擬也面臨著較大的困難。在普通的低速湍流燃燒中,壓力可以近似為常數,進而引入反應標量概念,使得研究得到簡化。但這種簡化在與爆轟相關的湍流燃燒中是不適用的,較高的馬赫數使與爆轟有關的湍流燃燒面臨高可壓縮性,尤其是流場中存在強間斷。爆轟波的高速使得波陣面和波後等相關流場具有較高的雷諾數,故流場中的最小流動尺度Kolmogorov尺度具有較小的值,而直接數值模擬採用的網格需小於該尺度,因而會面臨較大的困難。而基於RANS方程的湍流模型得到的是流場引數的平均量,其值無法反映真實的流場狀況。因此,從精度和計算量的綜合考慮,大渦模擬更適合研究與爆轟有關的湍流燃燒,但其面臨的難點是湍流的亞網格模型的封閉和燃燒模型的封閉。此外,高速流動使得濾波後的能量方程(或平均能量方程)中出現高速源項,該項體現了壓縮波與膨脹波對流場的影響,是無法求解的,也需要採用一定的模型進行封閉。高溫高壓的環境使得真實化學反應更加複雜,現有的湍流燃燒模型針對的大多是簡化反應機理,而對於反映真實燃燒情況的基元反應則面臨較大的困難,這是基元反應中差別懸殊的反應速率引起的剛性問題造成的。本文對爆燃轉爆轟和爆轟波結構中涉及的湍流燃燒的研究現狀進行了分析和評述,並對未來的研究進行了展望。
1、爆燃轉爆轟中的湍流燃燒
1.1爆燃轉爆轟的典型過程
利用較小的點火能量,生成層流火焰,在適當的條件下,火焰持續加速,形成激波,甚至可發展為爆轟。這種以弱點火生成爆轟的現象稱為爆燃轉爆轟。影響爆燃轉爆轟的因素很多,點火方式、邊界條件和變換機制等皆可以影響其轉換過程[7]。因此,爆燃轉爆轟的過程也不具有唯一性。
一端封閉的管,於封閉端點火,只要足夠長,燃燒便可轉換為爆轟,該轉換過程可反映爆燃轉爆轟的主要環節,常被視作爆燃轉爆轟的典型過程。圖1是利用火焰自發光拍攝的,爆燃轉爆轟的狹縫掃描照片[3]。可燃氣為C2H2+O2。在封閉端,用熱射流點火,點3為點火點,曲線4表示層流火焰加速軌跡,曲線5處的發光區域逐漸變寬,表示湍流火焰加速軌跡,點6表示突然轉變為爆轟,隨後,形成過驅爆轟7,逐漸衰減為CJ爆轟。同時,出現回傳爆轟,即曲線9,在曲線7與9之間的區域內,週期出現光亮的彎曲橫線8,此為壁面反射的橫向激波對燃燒產物氣體進行壓縮的結果。從點火點3到爆轟突發點6之間的距離稱為轉換距離,它不僅決定於燃料特性,還決定於點火方式和邊界條件。
圖1燃燒產物射流形成爆轟的狹縫掃描照片
圖2為爆燃轉爆轟過程的高速分幅紋影照片[8]。可燃氣為H2+O2,封閉端點火,在邊界作用下,失穩加速,形成湍流火焰,表面呈現精細的胞格狀結構。湍流火焰使燃燒進一步增強,燃燒產物膨脹,壓縮火焰前的未燃氣體,形成系列壓縮波,壓縮波的追趕最終形成激波。在壁面附近的湍流火焰內,出現區域性爆炸,形成爆轟波,最終發展成強爆轟,同時出現回爆。
圖2燃燒轉爆轟的分幅紋影照片
因此,爆燃轉爆轟的典型過程大致可以分為三個階段[5]:
1)燃燒。弱點火後,生成層流火焰,在邊界作用下失穩加速。加速火焰與壁面具有正反饋作用,使火焰持續加速,乃致猝發湍流,形成湍流火焰,導致燃燒速度進一步增強。
2)爆燃。燃燒產物的膨脹對火焰陣面前的介質有壓縮作用,形成系列壓縮波,最終發展成激波,該誘導激波隨火焰的持續加速而不斷增強。在此階段,誘導激波與火焰面形成一複合波,且激波傳播速度大於火焰傳播速度,燃燒是透過分子擴散進行的。誘導激波強度決定於火焰燃燒速度,而燃燒速度決定於邊界條件。
3)爆轟。加速火焰形成的誘導激波足夠強時,激波預壓區可能出現區域性爆炸,形成爆轟泡,使燃燒突然轉變為強爆轟。強爆轟不穩定,逐步衰減為穩定傳播的CJ爆轟。此時,激波與火焰耦合,形成激波-火焰耦合波。激波強度決定了火焰速度,兩者的傳播速度相等。
在爆燃轉爆轟過程中,第一階段的火焰加速和第二階段誘導激波的增強均與湍流燃燒密切相關,國內外大量的實驗已證實了這一點[6,7,8,9,10,11,12,13,14,15]。
1.2湍流對火焰加速的影響
火焰在直管中傳播時,燃燒產物的膨脹導致波前質點的流動,該流動稱為背景流場。由於黏性,背景流場在壁面附近形成黏性邊界層,即出現速度梯度場。此時,火焰傳播時,陣面不同部分傳播的環境不同,因而具有不同的傳播速度,從而使得火焰變形。火焰變形導致燃燒面積增大,燃燒速率增加。加速火焰容易失穩,燃燒速率會進一步增加。背景流場的速度隨著的燃燒速率的增加而增加,這又導致流場雷諾數的增加。當雷諾數大於臨界值時,背景流場出現湍流,如圖3所示[9],湍流邊界層使燃燒速率急劇增加,火焰傳播速度也愈大。背景流場的雷諾數愈大,湍流愈強,燃燒速度愈快,使火焰持續加速,在火焰前面形成激波,如圖4所示[10,11],當出現熱點時,出現區域性爆炸,形成爆轟。
圖3加速火焰前方邊界層的陰影照片
如在火焰的傳播路徑上設定障礙物,將會加劇火焰的失穩,其間涉及不同的火焰失穩機制,如Taylor不穩定,Richtmyer-Meshkov不穩定,Helmholtz不穩定和Landau-Darrieus不穩定等。當火焰失穩達到一定程度時,過度的變形必然猝發湍流。湍流使火焰變形更為嚴重,並大大增強輸運能力,使已燃流團與未燃流團充分摻混,從而大幅增加燃燒速度。
圖4乙烯-氧氣混合物的DDT過程的陰影照片
圖5為障礙物作用下,火焰失穩並誘發湍流的實驗照片。其中圖5(a)為薄片障礙物[3],圖5(b)為方塊障礙物[12]。管道中的障礙物減少了通道中的流動面積,導致背景流場的流動加速。因此,受背景流場的影響,火焰在抵達障礙物之前已經變形,上部的傳播速度明顯大於下部,流場的這種特性會導致火焰失穩(主要為Taylor不穩定)。對於薄片狀障礙物(圖5a),火焰跨越障礙物後,頭部出現湍流燃燒,湍流刷明顯可見。當障礙物具有一定厚度時(圖5b),障礙物與上壁面形成了狹長通道,火焰穿越時,變形火焰的頭部依然保持流向傳播,但底部為橫向傳播(向壁面逼近)。由於火焰的壓縮作用,橫向傳播的火焰在狹長通道中形成了來回振盪的壓縮波,從而導致橫向火焰失穩,形成湍流燃燒,使燃燒充滿狹長通道,見圖5(b)的最後一幅照片。背景流場中的氣體,在狹長通道中加速後,以射流形式離開障礙物,在障礙物背部形成帶渦環的繞流(Helmholtz不穩定),於是,湍流火焰也具有渦環結構,帶有繞流特性[5]。
圖5障礙物作用下火焰的傳播
障礙物誘導的湍流火焰,一般是不能自持的,一旦撤銷誘發湍流的外部因素,火焰將減速。如果重複設定障礙物,由於障礙物對流動的影響與火焰加速之間存在的正反饋的機制,火焰可持續加速(如圖6所示[7]),達到一定程度,會誘發爆轟的形成。
圖6阻塞比為0.6時,氫氣-空氣混合物中火焰傳播的陰影照片
爆燃轉爆轟是個比較複雜的物理化學過程,包含湍流燃燒、壓縮波反射、激波邊界層以及熱點自爆炸等現象,該過程不但具有強烈的非線性,還存在範圍寬廣的時空特徵尺度。實驗得到的資料有限,如需對該過程進行更深入的瞭解,需要藉助數值計算。採用數值計算時,不但需要合適的湍流燃燒模型、高解析度的捕捉激波格式以及尺度極小的網格等,還需處理方程剛性等問題,因此面臨諸多挑戰。但是因為爆燃轉爆轟的研究具有特殊的理論和實用價值,而數值計算是研究該過程的有效手段,所以儘管面臨很多困難,人們還是進行了大量的工作。
Ivanov對長方形管道中氫氣-氧氣混合物的DDT過程採用了三維直接數值模擬[16],化學反應模型採用詳細基元化學反應模型,網格尺寸為25μm。圖7代表了火焰在邊界層的作用下失穩加速、誘導激波的過程,圖7(a)是火焰面和激波的三維流場結構,圖7(b)是相應的x-y截面雲圖和流線圖。初始的不規則擾動誘發了火焰刷,火焰加速產生的壓縮波不斷追趕,逐漸在火焰前方合併成激波,波後流動引起的邊界層使得火焰面發生皺褶。值得關注的是,火焰和其前方的流動一直是層流,直到形成爆轟。圖8(a)和圖8(b)是根據圖7的流場繪製的火焰加速的計算陰影圖,從圖上看,似乎形成了“湍流火焰刷”,與圖8(c)的實驗陰影圖[17]定性上是一致的,然而,根據圖7的三維數值結果,無論是火焰還是流動,均是層流,圖8(a)和8(b)中的“湍流”效果是光束透過胞格層流火焰折射形成的,這意味著三維的層流火焰經過二維的投影后,可以得到湍流效果,這可能造成對該類現象研究的誤導。
圖7火焰在方管加速過程中,火焰結構和壓縮波(激波)的作用
圖8火焰面附近流場的計算陰影圖
Poludnenko採用更細的網格對非受限空間內的DDT過程進行了直接數值模擬[18,19],網格尺寸為δL,0/16,其中δL,0為層流火焰厚度,可燃氣採用甲烷-空氣混合物,化學反應模型採用單步化學反應。圖9為湍流火焰發展和DDT過程,其中左圖為燃料質量分數的等值面,右圖是壓力場。火焰加速引起的背景流場產生的高強度湍流與火焰相互作用形成的正反饋過程使得火焰不斷加速,當湍流火焰速度超過CJ爆燃速度時,火焰非常不穩定,極易形成爆轟。湍流火焰速度與最大壓力的發展歷程如圖10所示,圖中黑實線代表湍流速度的發展變化,紅虛線代表最大壓力的發展變化。從理論上來說,CJ爆燃速度是滿足守恆方程的最大爆燃速度。而湍流火焰速度依賴於湍流強度和湍流火焰結構,因此可以超過CJ爆燃速度。根據反應流守恆方程,當燃燒速度超過CJ爆燃速度時,無法形成穩定的爆燃波,流動需要發展,產生激波,達到滿足守恆方程的一種新的穩定狀態。最終,出現兩種狀態,一種是火焰呈現脈衝不穩定,火焰速度在CJ爆燃速度上下週期性的振盪,另一種是形成CJ爆轟。
圖9在等當量比的甲烷-空氣混合物中,湍流火焰和轉變成爆轟的演變
圖10實驗和數值模擬中,壓力和湍流火焰速度的變化曲線
Gamezo採用二維N-S方程對有障礙物的管道中的DDT過程進行了數值研究[20],並討論了障礙物間距對DDT過程的影響,可燃氣體採用氫氣-空氣混合物,化學反應模型採用單步化學反應,最小網格尺寸為1/512cm。圖11為火焰透過有障礙物的管道時加速及DDT形成過程的溫度等值雲圖。障礙物的作用使得火焰捲曲變形,燃燒面積增加,火焰加速,伴隨著火焰的不穩定,如激波與火焰作用的Richtmyer-Meshkov不穩定。燃燒產物以熱射流形式穿過障礙物上方的狹窄通道,由於Helmholtz不穩定,形成剪下層和渦環結構,火焰進一步加速。障礙物的持續作用,使得爆轟最終形成。然而,此計算始終基於層流模型。變形層流火焰與湍流燃燒一樣,也可使火焰持續加速,進而誘導激波。因此,層流燃燒計算也能使燃燒轉為爆轟,但計算結果描述的物理過程與實驗並不吻合。這是由於火焰嚴重變形時,已發展成湍流燃燒,不再是層流燃燒,若採用直接模擬,網格尺度應為Kolmogorov微尺度,遠小於該文章的網格尺寸。
Goodwin透過數值模擬對障礙物阻塞比對管道內DDT的影響進行了二維和三維研究[21,22]。二維數值模擬採用的最小網格是3.3μm,最大網格是53.3μm,三維數值模擬採用的最小網格是6.67μm,最大網格是53.3μm,可燃氣體採用氫氣-空氣混合物,化學反應模型採用一步反應模型。圖12為不同阻塞比的管道中,火焰加速和DDT形成的二維溫度等值雲圖。隨著阻塞比的降低,可觀察到兩種不同的DDT機理。對於阻塞比為0.5時,在障礙物處形成馬赫反射,馬赫幹後形成熱點,誘發爆轟;阻塞比為0.1時,激波在邊界層處多次反射,形成能量聚焦,誘發爆轟;對於高阻塞比0.8,爆轟的誘發同時具有上述兩種機理。圖13為不同阻塞比下,火焰前鋒隨時間的變化。障礙物的阻塞比越大,對火焰的擾動越厲害,越容易誘發湍流,進而更容易形成爆轟。圖14為阻塞比為0.1時,火焰加速和DDT形成的三維反應物質量分數等值面圖。層流火焰透過障礙物時開始加速,在t=0.071ms時,經過第三個障礙物,此時,在管道的下側壁面附近開始形成湍流火焰結構,經過第六個障礙物時,形成充分發展的湍流火焰,t=0.102ms時,在下壁面開始起爆。與二維數值模擬的結果相比,火焰加速和DDT形成的過程是相似的。但是,在三維的數值計算結果中,湍流使得火焰加速更快,也就越早形成爆轟。圖15表示阻塞比為0.1時,二維和三維數值計算的火焰鋒面位置隨時間的變化曲線。對於二維數值計算的DDT過程,經過13個障礙物,大約t=0.1472ms,開始形成爆轟波,而三維數值計算的DDT過程,只需經過9個障礙物,用時0.102ms就可以形成爆轟波。這也表明,不考慮湍流效應的DDT過程,其計算結果無法用來對DDT進行定量預測,比如DDT距離。
圖11有障礙物的管道中,火焰加速和DDT過程
圖12不同阻塞比的二維管道中,火焰加速和爆轟形成過程
圖12不同阻塞比的二維管道中,火焰加速和爆轟形成過程
圖13不同阻塞比下,火焰面前端隨時間變化
圖14阻塞比為0.1的三維管道中,以反應物質量分數的等值面表示火焰加速和爆轟形成過程
儘管之前的直接數值模擬研究採用了較細的網格,但是湍流中的最小尺寸Kolmogorov尺寸卻沒有提及。Emami採用大渦模擬對氫氣-空氣的DDT過程進行了數值模擬[23],亞網格的湍動能採用輸運方程描述[24],燃燒模型採用ATF方法,化學反應採用9組分27步詳細反應機理模型,採用ISAT方法,以減小詳細化學反應帶來的計算消耗。圖16和圖17為火焰在障礙物之間傳播時的計算陰影圖,燃燒產物的膨脹在火焰的前方形成壓縮波,該波在與障礙物和壁面的反射中不斷加強,形成激波,激波隨後與障礙物附近的渦相關作用,已有的研究表明,激波-渦和激波-湍流的相互作用可以增加湍動能和渦量,同時減小流動的長度尺度[25],因此障礙物附近的湍流得到增強,進一步使火焰加速(圖16)。隨著激波與渦的作用,激波及其反射激波在壁面和障礙物上反射,火焰面的前方出現複雜的湍流區域(圖17中的2.5ms)。當火焰傳播速度達到壓縮過的未燃混合物的聲速時,遠處障礙物的下游流動沒有得到加強,反而逐漸衰減。因此,障礙物前方沒有形成較強的渦量場,該現象在圖18中可以觀察到,圖18中依次為計算紋影圖、熱量釋放圖、湍流強度圖和渦量圖,時間依次為2.64、2.65、2.67ms。在2.64ms時刻,火焰前鋒透過第十個障礙物,此時,火焰沒有與壁面的反射激波作用,火焰鋒面的熱量釋放率和湍流強度較低。當火焰速度達到未燃物的聲速時,遠處障礙物的流動減弱,湍流強度降低,因此,障礙物與火焰的強作用沒有發生。在2.65ms時刻,壁面反射的激波開始與火焰面作用,導致能量釋放、湍流強度和渦量均急劇增加。在2.67ms時刻,火焰前鋒到達第11個障礙物,火焰與更強的反射激波作用,使得能量釋放進一步增加,這與Ciccarelli提出的快速火焰傳播機理[26]是一致的。基於大渦模擬計算的資料,火焰透過障礙物加速時,涉及的湍流燃燒處於不同的湍流燃燒區域,如圖19所示,其中19(a)表示Peters提出的湍流燃燒分割槽[27],19(b)表示Pitsch提出的針對大渦模擬的修正的湍流燃燒分割槽[28]。在這兩幅分割槽圖中可以觀察到,傳播的火焰位於“薄火焰區”(Ka>1)和“厚火焰區”(Ka>100)。隨著火焰的傳播,湍流燃燒進入“厚火焰區”,此時,燃燒速率由化學反應控制,而不是由混合控制,這表明計算採用的ATF模型是合適的。
圖15阻塞比為0.1、高度為0.16cm的管道中,二維和三維數值模擬的火焰面前端隨時間變化
圖16火焰在障礙物5和7之間傳播的計算陰影圖
圖17火焰在障礙物7和9之間傳播的計算陰影圖
圖18、熱量釋放速率、湍流脈動速度和渦量的變化圖
圖19在預混湍流燃燒分割槽圖中,火焰在有障礙物的管道中傳播時的位置
2、爆轟波結構中的湍流燃燒
2.1弱不穩定與強不穩定的爆轟波
爆轟波在管道中傳播時,在管壁會留下魚鱗狀的胞格結構[37]。這些胞格結構與爆轟波陣面上激波的相關作用有關,如圖20(a)所示,其中橫波對爆轟波的傳播起到關鍵的作用。每次橫波相碰時,其距離大約等於爆轟波結構中反應區寬度的100倍左右,該距離稱為爆轟胞格寬度,如圖20(b)所示,它是可燃系統的本徵值,是爆轟的動力學引數[38],反映了系統氣體動力學和化學反應動力學之間的非線性關係。
爆轟在本質上是不穩定的,胞格結構較規則的可燃系統稱為“弱不穩定”胞格結構不規則的可燃系統稱為“強不穩定”[39],如圖21所示。穩定性強弱與可燃系統的活化能密切相關。NG提出了一個穩定引數來區分爆轟波的穩定性[40],該引數可表示為:
其中,,表示誘導區的溫度感度,Ts為引導激波溫度。ΔI和ΔR分別為誘導區和反應區的長度。χ愈小,爆轟愈穩定。
圖20爆轟波的結構
圖21初壓為20kPa下的爆轟胞格
對於弱不穩定爆轟的可燃系統來說,混合物具有較低的活化能,比如H2+O2、C2H2+O2或者氬稀釋的燃料-氧氣混合物。低活化能使激波後的未燃氣體有較短的點火延遲,能量可在較短的時間釋放,爆轟波陣面處的燃燒呈現層流燃燒。此時,弱不穩定爆轟的傳播僅由激波壓縮來驅動,其結構可以較好地透過波後氣體的點火延遲歷程來預測,而輸運效應可以忽略[41]。
對於強不穩定爆轟的可燃系統來說,混合物的活化能較高,反應誘導區較寬,三波點附近的剪下層及各種不穩定使得波陣面處的燃燒呈現湍流燃燒[42,43,44,45,46]。此時,爆轟波的傳播由激波壓縮和湍流輸運共同維持,這類混合物主要是碳氫燃料和氧氣或其他氧化劑組成,形成的胞格尺寸有較寬廣的範圍。
2.2強不穩定的爆轟波結構中的湍流燃燒
已有的實驗表明,對於強不穩定的爆轟波,激波陣面脈動較大。馬赫幹較強,波後的可燃氣體在較短的時間內完全燃燒,而入射激波的強度較弱,波後的誘導區較長,反射橫波分為兩部分,一部分在入射激波壓縮後的未燃氣體中傳播,使其燃燒,另一部分在燃燒產物中傳播。同時,橫波與入射激波後的火焰面作用,產生Richtmyer-Meshkov(RM)不穩定,加強了區域性燃燒速率。在反射橫波與馬赫幹後的燃燒產物具有不同的速度,因此在這兩道波間出現一剪下層,該層是由Kelvin-Helmholtz(KH)不穩定引起的,如圖22所示,其中圖22(a)是實驗紋影圖,圖22(b)是流場簡圖。入射激波後的火焰面為湍流燃燒,剪下層是一道接觸間斷,也呈湍流狀態,是湍流剪下層[43]。
圖22甲烷與氧氣混合物在初壓3.4kPa下的爆轟波的精細結構
此外,由於入射激波較弱,可燃氣體不能完全燃燒,在波陣面的後部形成被燃燒產物包圍的未燃氣團,如圖23所示,未燃氣團清晰可見。該氣團被燃燒產物包圍,其大小和距離波陣面的位置隨活化能的增加而增加。實驗表明,這些未燃氣團的燃燒速度非常快,其數量級明顯快於定常激波的點火時間。因此,ZND模型不能預測前導激波後的流場特性。這意味著波後的未燃氣團與周圍的燃燒產物以湍流混合的方式進行燃燒,而不僅僅是激波壓縮引起的燃燒。這些未燃氣團仍然在爆轟波的流體力學結構中,即激波陣面與平均聲速面之間,因而壓力脈衝可以影響爆轟波陣面[6]。而且,三波點對未燃氣團的燃燒動力過程起到關鍵的作用,這是由於三波點不僅能提供高溫高壓的環境,而且能加強湍流混合。
圖23甲烷與氧氣混合物在初壓3.4kPa下的爆轟波的精細結構
目前為止,數值研究表明,在精度足夠的條件下,中等活化能的不規則爆轟波結構可以較好地透過數值求解Euler方程得到[47,48]。然而,更多的數值研究表明,採用同樣的方法求解帶有較高活化能的不規則混合物時,取得的成功有限[6]。儘管這種努力使人們對理解激波壓縮或湍流運動對爆轟波傳播的影響有限,得到的解也受限於精度的影響,不能收斂於唯一解。但是,這種研究證實,波陣面存在較長的誘導時間,其數量級是實驗中觀察到的100倍左右,未燃氣團透過數值演算法的精度誤差引起的擴散迅速地燃燒。一些研究者試圖透過直接數值求解Navier-Stokes(N-S)方程,得到流場涉及到的完整譜尺度,包括分子擴散效應。不幸的是,這些研究表明,對二維問題涉及的全譜尺度的求解,得到的數值解不足以正確地反映未燃氣團的燃燒速率[49]。因此,全尺度的直接數值模擬只能針對單個的事件,比如三波點的碰撞[50]。此外,湍流本質上是三維的,湍流的運動滿足能量串級,其耗散取決於第三個方向的拉伸[51]。
Radulescu分析了高活化能的不穩定爆轟波的流場中的Kolmogorov尺度,認為Kolmogorov尺度是爆轟波ZND模型誘導區長度的1×10-4倍,意味著誘導區內至少有1×104個網格,網格尺度只有達到精度,才能準確模擬爆轟波結構中的湍流擴散過程,目前的計算能力還無法完成這種計算[6]。因此,目前數值模擬無法透過直接模擬來求解爆轟波中的湍流燃燒,而大渦模擬(LES)兼顧求解精度和計算能力的平衡,其中大尺度的運動透過直接數值求解N-S方程,無法求解的小尺度湍流採用建模的方法[52,53,54,55,56,57,58]。
雖然二維流動只能描述大尺度的流體運動,Radulescu採用二維Euler方程對高度不穩定爆轟波結構整體特性進行了數值研究,如圖24所示。在爆轟波陣面後方也出現了未燃氣團,橫波與未燃氣團作用,不會明顯改變氣團的形狀,這與實驗中觀察到是一致的。但是,該未燃氣團的燃燒是透過數值擴散進行,速度較慢,無法維持激波的自持傳播[43]。
Mahmoudi對不穩定爆轟波的結構分別採用Euler方程、Navier-Stokes方程和大渦模擬進行了數值模擬[49]。大渦模擬中亞網格模型採用的是Smagorinsky渦黏模型,化學反應模型採用濾波後的Arrhenius定律,即假定湍流的亞網格時間小於所有的化學反應時間。圖25是密度等值雲圖,圖25(a)~25(c)分別為Euler方程、N-S方程和大渦模擬計算的結果,Euler方程和N-S方程計算的結果定性是一致的,但是N-S方程的結果中KH不穩定引起的小尺度渦被分子擴散所抑制。採用大渦模擬計算的結果,由於湍流擴散的存在,KH不穩定引起渦的尺度更加小,並且與射流有關的長舌狀未燃氣體幾乎消失,這使得該射流與激波作用形成的第二三波點B也不存在,結構更加規則些。圖26是相應的壓力等值雲圖,由於湍流使未燃氣體的快速消耗,橫波未與未燃氣體作用,因此區域性最高壓力比Euler方程和N-S方程計算的均低,且橫波直接在壁面上反射。透過與Kiyanda的實驗[59]對比(圖27),大渦模擬計算的結果吻合的更好。
Mahmoudi的研究雖然對爆轟波的結構進行了較好的模擬,但其對反應封閉問題的處理採用了一定的假設,爆轟波後面的燃料的反應速率的求解精度還是有問題的,該研究工作是將湍流混合與燃燒速率分開單獨求解。隨後,Maxwell採用CLEM-LES方法對爆轟波結構進行了數值模擬[56,57,58],其中N-S方程採用LES,組元守恆方程採用線性渦模型[60,61,62,63,64](LinearEddyModel,LEM)。計算時,需要採用兩套網格,LES在大尺度主網格中進行,基於LEM的組元守恆方程在小尺度亞網格中進行,湍流擴散用隨機翻轉模型處理,該方法的主要優點是可以同時處理化學反應與同一尺度的流動,不需要對反應速率進行假設。圖28是爆轟波結構的數值計算結果與實驗結果,其中圖28(a)為Maxwell數值計算結果,圖28(b)為Kiyanda的實驗自發光圖片[65]。爆轟波後部出現明顯的未燃氣團,該氣團的湍流火焰速度可透過數值結果計算得到。對於氣團,區域性湍流火焰速度可以採用下式計算:
圖24數值實驗中的密度等值雲圖
圖25熱力學引數:Ea/RT0=20,Q/RT0=50,γ=1.2,精度為半個反應區600網格時,爆轟波結構的密度等值線雲圖
圖26熱力學引數:Ea/RT0=20,Q/RT0=50,γ=1.2,精度為半個反應區600網格時,爆轟波結構的壓力等值線雲圖
圖27爆轟波的反應區結構的紋影圖
其中,是反應物的消耗速度,ρu是未燃物密度,Ac是未燃物的面積。整個湍流火焰速度可以透過在氣團表面對火焰速度進行空間和時間的系綜平均:
為了得到區域性湍流混合速率對湍流火焰速度的影響,圖29表示平均湍流火焰速度St/SL隨湍流強度u′/SL的變化曲線,對於每一湍流強度,火焰速度採用u′/SL±0.5之間的平均值。結果表明,平均湍流火焰速度隨著湍流強度呈線性增長,這與Abdel-Gayed的實驗結果[66]是一致的。
圖28爆轟波的精細結構
圖29根據數值計算結果與Abdel-Gayed的實驗結果,湍流火焰速度隨湍流強度的變化
3、總結與展望
爆轟的生成和傳播是爆轟的兩個重要現象,其中的爆燃轉爆轟(DDT)和強不穩定的爆轟波結構是關注的重點,目前主要採用實驗觀測和數值模擬研究。在DDT的研究中,燃燒產物的膨脹導致燃燒波前質點的流動,形成背景流場,無論是管道中的邊界層還是障礙物均對背景流場施加影響,使火焰面變形加速,燃燒速率增加,而背景流場的速度隨著的燃燒速率的增加而增加,這又導致流場雷諾數的增加。當雷諾數大於臨界值時,背景流場出現湍流,形成湍流燃燒,當燃燒速率超過CJ爆燃速率時,流場極不穩定,或出現熱點形成區域性爆炸中心,或出現強激波誘發燃燒,最終形成爆轟。在強不穩定的爆轟波結構研究中,較高的活化能使得反應誘導區較寬,三波點附近的火焰面和剪下層出現了湍流,加強了燃燒速率和產物之間的混合速率。此外波後的未燃氣團也出現了湍流燃燒,燃燒釋放的壓力脈衝有可能會影響爆轟波的結構,這取決於未燃氣團的位置。無論是DDT中火焰的加速,還是強不穩定的爆轟波結構中激波與火焰的耦合,湍流在其中都起了關鍵的作用,因此,在爆轟的未來研究中需要結合其自身特點開展研究。
爆轟是一種超聲速燃燒,具有高馬赫數、高雷諾數和高溫高壓的特點。對該物理現象的描述可以採用反應流N-S方程(包括質量方程、動量方程和能量方程)處理,這是一組偏微分方程,具有不適定性(方程不穩定導致的湍流燃燒)和奇異性(跨聲速中的聲速點),至今沒有解析解,這屬於數學層面的難題,在未來相當長的時間可能也無法得到解析解,而爆轟的重要特性顯然與方程的這種不適定性和奇異性密切相關。關於爆轟現象的實驗測試,目前主要還是主要採用光學測試技術,這是一種非接觸式測量技術,它對流場的干擾小,有著高精度、高靈敏度、快速和實時測量的特點,能對爆轟波流場進行清晰的測試,其結果多用於爆轟現象的定性討論和少量的定量測試,比如實驗測量的爆速,一直是判斷爆轟是否形成的標準引數。對於爆轟現象的定量分析還得更多借助於數值模擬,模擬方法可以分為直接數值模擬、基於RANS的湍流模型和大渦模擬。直接數值模擬具有流場解析度最高、資訊量最大等優點,其缺點也很明顯,比如需佔用較大的計算資源,因此,該方法主要用於小尺度的基礎研究。基於RANS的湍流模型得到的流場資料不是流場的真實資訊,而是流場引數的平均值,可以反映流場的整體結構,因此,該方法可以用於爆轟的工程應用,比如各種爆轟推進系統。大渦模擬是介於直接數值模擬和基於RANS的湍流模型之間的湍流數值方法,無論是基礎研究還是工程應用,該方法都具有較大的潛力,其面臨的難題是各種模型的封閉問題,比如湍流的亞格子應力模型、燃燒模型、高速流動源項的封閉模型等。由於組分守恆方程中含有溫度的指數項,故燃燒模型的封閉是其關鍵難題。線性渦模型(LEM)已被用來處理爆轟中的燃燒問題,並取得了較好的效果。此外,Flamelet模型、TPDF模型和ODT(模型已用於高速湍流燃燒,並取得了一定成果,未來也可用於爆轟的模擬中,這些值得進一步研究。