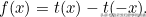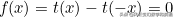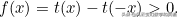在任何一個時刻,地球赤道上都有兩個溫度相同的點。
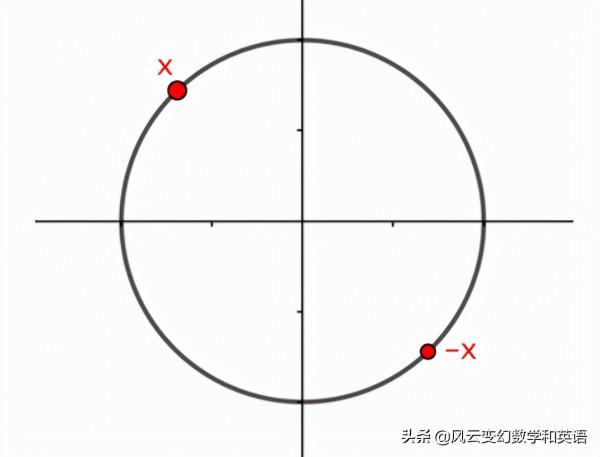
我們是怎麼知道的?這裡有個證明。我們來看看赤道面,它在赤道處穿過地球。赤道是平面上的一個圓,我們可以在平面上選擇一個座標系,使點(0,0)位於赤道的中心。對於赤道圓上的每一個點x,都有一個點-x,它與x完全相反。
赤道上的每個點,都有一個溫度,t(x)。我們可以假設函式t,為每個點分配一個溫度,是連續的。這是因為當你在地球上移動時,溫度不會突然上升或下降。
現在考慮函式
它也是連續的。
如果這個函式在某點x上等於0,那麼我們就證明完了,因為如果
那麼
所以x的溫度和-x的溫度是一樣的。
如果f(x)在任何地方不等於0,那麼我們假設(不失一般性)存在一個點x,在這個點上f(x) >0, 所以
這隱含著
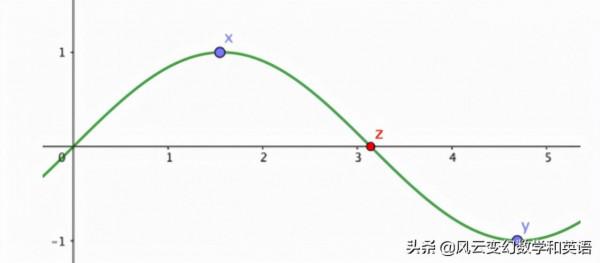
有一個結論,叫做介值定理,它說的是如果一個連續函式在它定義域的某一點大於0,而在另一點小於0,那麼它在這兩者之間的某一點一定等於0。
因為f(x) >0, f(-x) <0, 所以一定有一點有使得f(y)=0:
這意味著
所以點y的溫度等於點-y.
這個結果實際上適用於地球上的任何圓周,不僅僅是赤道。