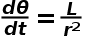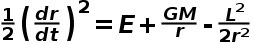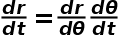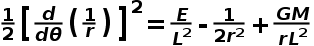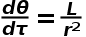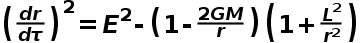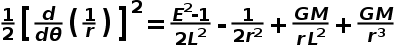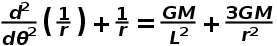如果你曾經在極座標系下推導行星在牛頓引力下的方程，你會得到：

角動量守恆

能量守恆

其中L和E分別是行星的角動量和能量，利用以下這個等式可以消去t：

可以得到軌道方程：

等式兩邊對θ進行微商，得到：

等式1

把1/r看成一個整體，我們就可以解出這個常規的微分方程，得到軌道方程。

廣義相對論中的行星軌道

廣義相對論中的能量守恆、角動量守恆與牛頓力學不同，此外還有一個四速歸一化條件：

能量守恆

角動量守恆

四速歸一化

其中我們採用了光速c=1的自然單位制度，τ是固有時。我們可以利用同樣的技巧消去dτ，等到方程：

同樣等式兩邊對θ進行微商，得到：

等式2

在天文學的精確測量之下，我們知道行星的軌道並不是像牛頓力學預測的那樣封閉的，在太陽系中水星的近日點進動效應最為顯著。每一百年水星的近日點進動5600''，扣除掉歲差和其它行星攝動的影響，牛頓力學預測的進動值與真實值還差43''。

等式2相比等式1，多了一個附加項3GM/r²，而這一項正是廣義相對論效應的體現，可以看成是牛頓理論的廣義相對論修正項。也正是有了這一項，讓我們可以解釋43''的差距。感興趣的同學可以自行解這個難度較大的非線性微分方程，然後就可以得到真正的軌道方程，代入資料就可以得到進動值。