帶電粒子在正交的勻強磁場和勻強電場(或重力場)所形成的複合場中運動,若所受洛倫茲力與電場力(或重力)不平衡,電場力(或重力)會改變粒子的速度,而速度的變化又會使洛倫茲力不斷變化,使粒子做複雜的曲線運動,它的軌跡不是圓,也不是拋物線,而是旋輪線,就是行駛的汽車輪子上某點的運動軌跡.
旋輪線的運動可以分解為繞圓心的圓周運動(母圓)和圓心的平動.
受速度選擇器的啟發,配速法就是“無中生有”配上一個速度,配上的速度所對應的洛倫茲力和電場力(或重力)抵消.
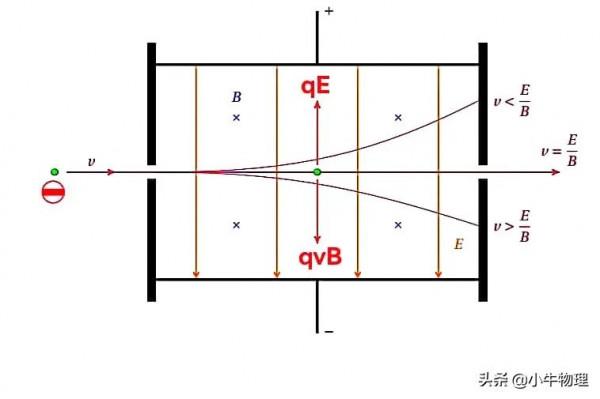
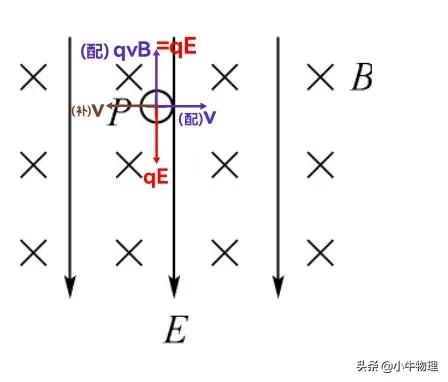
帶電粒子在速度選擇器中的運動
如果粒子的速度v=E/B,就有qvB=qE,粒子軌跡為直線,若粒子的速度大於或小於E/B,粒子的軌跡就不再是直線而是比較複雜的曲線。這種曲線既不是圓弧也不是拋物線,數學上把這種軌跡稱為“擺線”、“最速降線”、“旋輪線”.
①繞圓心轉動速度等於圓心平動速度(相當汽車輪子不打滑)
②繞圓心轉動速度大於圓心平動速度(相當汽車輪子原地打轉)
③繞圓心轉動速度小於等於圓心平動速度(相當汽車輪子剎車滑行)
常用方法:動能定理和牛頓第二定律
特殊方法:配速法
配速法步驟:
①找到電場力(或重力)
②配上一個電場力(或重力)等大反向的洛倫茲力
③配上一個和所配洛倫茲力對應的速度
③補償所配的速度
特點:
①最大速度圓心平動速度和繞圓心轉動速度之和;最小速度圓心平動速度和繞圓心轉動速度之差.
②最高點或最低點距圓心為R.
③一拱週期為2πm/qB.
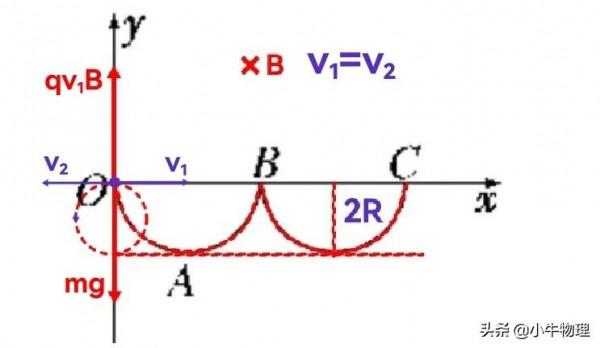
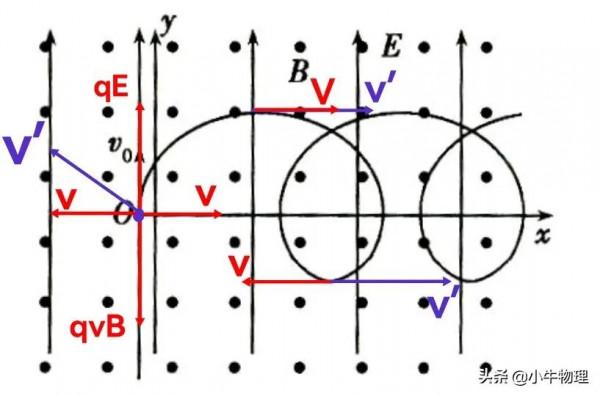
例題:如圖所示,勻強電場E的方向豎直向下,勻強磁場B的方向垂直紙面向裡,粒子質量為m(重力不計),電荷量為+q,以水平速度v₀從左側射入,且V₀>E/B.
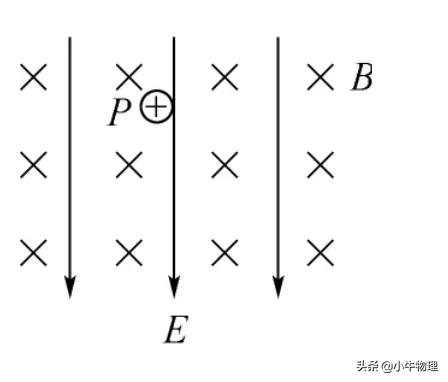
例題:如右圖所示,在垂直紙面向內的勻強磁場B和豎直向下的電場E中,有一質量m、帶電量十q粒子由點P無初速釋放,請分析它的運動,求:
(1)粒子向下運動的最大位移dm。
(2)粒子運動過程中的最小速度和Vmin最大速度Vmax
【解析】
【軌跡】
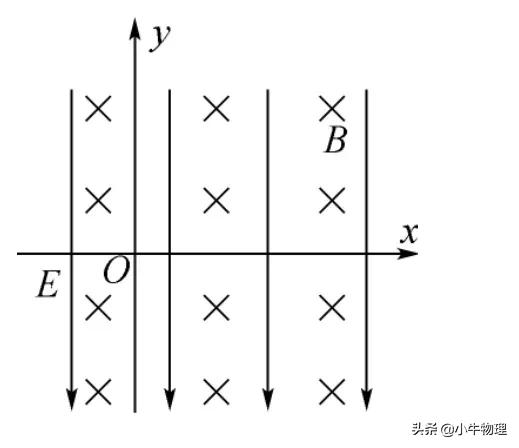
例題:如圖所示,二維座標系中存在著垂直紙面向內的勻強磁場B和豎直向下的勻強電場E,一電子從座標原點處靜止釋放,求電子在y軸方向運動的最大距離yₘ。(電子的重力不計)。
例題:如圖所示,xOy座標平面在豎直平面內,x軸沿水平方向,y軸正方向豎直向上,在圖示空間內有垂直於xOy平面的水平勻強磁場.一帶電小球從O點由靜止釋放,運動軌跡如圖中曲線.關於帶電小球的運動,下列說法中正確的是(BD)
A.OAB軌跡為半圓
B.小球運動至最低點A時速度最大,且沿水平方向
C.小球在整個運動過程中機械能不守恆
D.小球在A點時受到的洛倫茲力大於重力
【解析】配上一個速度v₁,使得qv₁B=mg,補償速度v₂=v₁,
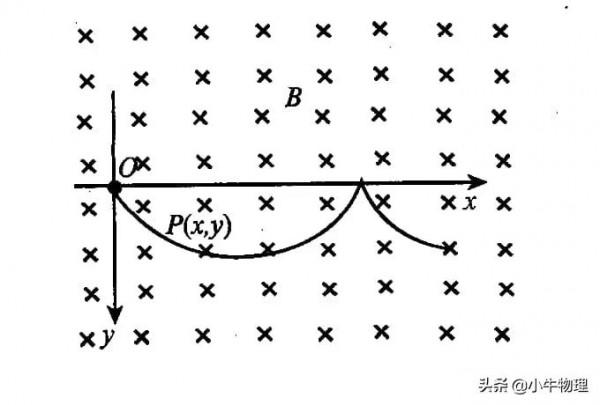
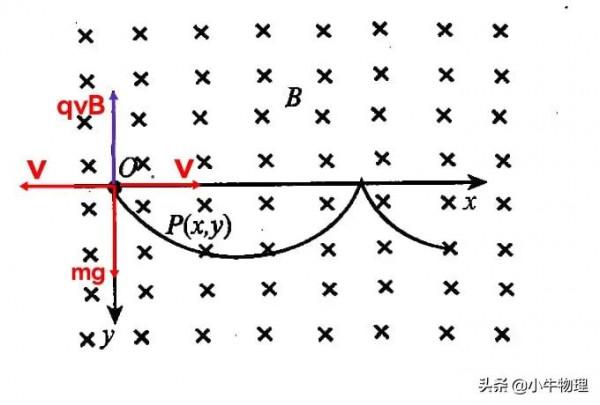
例題:在場強為B的水平勻強磁場中,一質量為m、帶正電q的小球在O點靜止釋放,小球的運動曲線如圖所示。已知此曲線在最低點的曲率半徑為該點到x軸距離的2倍,重力加速度為g。求:
(1)小球運動到任意位置P(x,y)處的速率v.
(2)小球在運動過程中第一次下降的最大距離ym.
(3)當在上述磁場中加一豎直向上場強為E(E>mg/q)的勻強電場時,小球從O靜止釋放後獲得的最大速率vₘ.
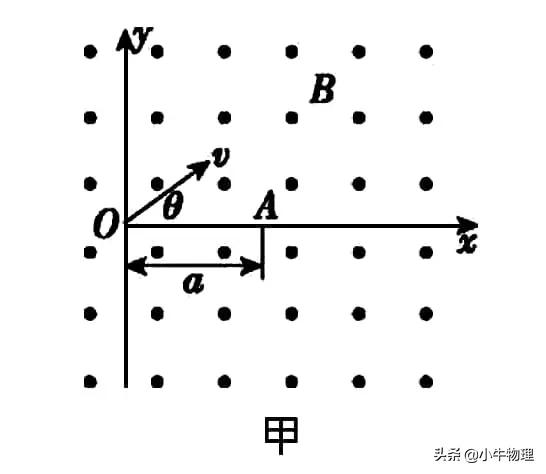
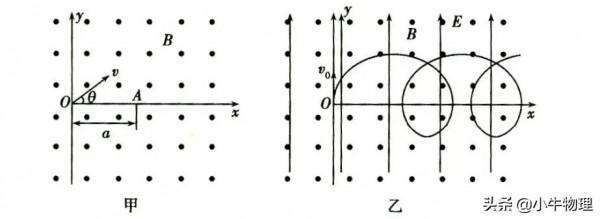
例題:如圖甲,空間存在一範圍足夠大的垂直於xOy平面向外的勻強磁場,磁感應強度大小為B。讓質量為m,電量為q(q>0)的粒子從座標原點O沿xOy平面以不同大小和方向的初速度入射到該磁場中。不計重力和粒子間的影響。
(1)若粒子以初速度v₁沿y軸正向入射,恰好能經過x軸上的A(a,0)點,求v₁的大小;
(2)已知一粒子的初速度大小為v(v>v₁),為使該粒子能經過A(a,0)點,其入射角θ(粒子初速度與x軸正向的夾角)有幾個?並求出對應的sinθ值;
(3)如圖乙,若在此空間再加入沿y軸正向、大小為E的勻強電場,一帶電粒子從O點以初速度v₀沿y軸正向發射,研究表明:帶電粒子在xOy平面內做週期性運動,且在任一時刻,粒子速度的x分量vₓ,與其所在位置的縱座標成正比,比例係數與場強大小E無關。求該粒子運動過程中的最大速度值vₘ。
【配速法】
例題:如圖所示,已知圓盤的半徑為R,豎直放在水平面上,開始時圓盤邊緣上的一點P位於座標原點,當圓盤在軌道水平面上沿直線以角速度ω無滑動向前滾動時,圓盤上的固定點P的運動軌跡為旋輪線。試推導圓輪邊緣上的固定點P的運動軌跡方程.
解析
利用幾何法推導方程。建立直角座標系如圖所示,開始時圓輪的頂點位於座標原點,與x軸相切,當圓盤沿水平軸勻速滾動時,設某時刻輪緣上固定點P的座標為P(x,y),半徑轉過的圓心角為θ,圓輪在x軸方向的位移等於弧長s=Rθ=Rωt,O′點座標為(ωRt,R).
P點的軌跡方程為:
(x-ωRt)²+(y-R)²=R²
P點的座標為:
x=s一Rsinθ=R(θ-sinθ),
y=R一Rcosθ=R(1-cosθ).
P點的引數方程為:
x=R(ωt一sinωt),
y=R(1一cos ωt).
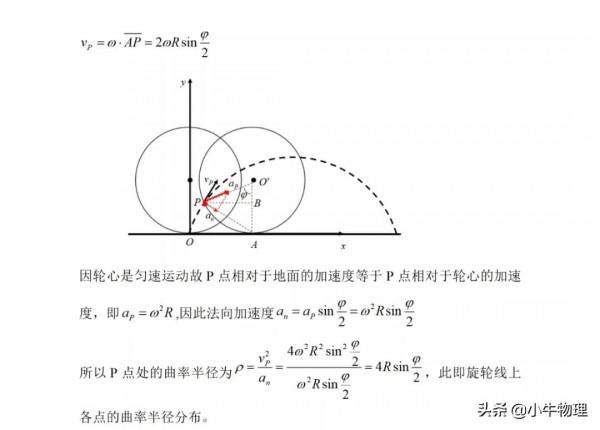
旋輪線曲率半徑:
旋輪線四個性質:
①旋輪線的長度等於旋轉圓直徑的4倍,是一個不依賴於π的有理數;
證明:在旋輪線上取一小段弧元ds,則(ds)²=(dx)²+(dy)²
因為:x=Rθ-Rsinθ;y=R-Rcosθ,所以dx=R(1-cosθ)dθ;dy=Rsin θdθ(ds)²=R²(1-cosθ)²(dθ)²+R² sin²θ(dθ)²=2R²(dθ)²(1-cosθ)=4R²(dθ)² sin²(θ/2)
ds=2 Rdθsin(θ/2),
旋輪線長度s=2R∫₀²ᴾᴵdθ=-4R∫₀²ᴾᴵdcosθ/2=8R
②旋輪線在弧線下的面積,是旋轉圓面積的三倍;
③圓上描出旋輪線的那個點,具有不同的速度,在某個特定的地方它甚至是靜止的;
④當彈子從一個擺線形狀的光滑容器的不同點放開時,會同時到達底部。