有理數“有道理”，無理數“沒道理”嗎？

大家在讀中學時都學習過有理數與無理數，這裡給出幾個數，你能立刻說出它是有理數還是無理數嗎？

怎麼樣，是不是很簡單？

不過，你有沒有想過，為什麼要稱這兩種數為“有理數”、“無理數”？你是否認為它們分別指的是“有道理的數”和“沒道理的數”？今天就和大家來聊一聊“有理數”和“無理數”名稱的由來。

1 有理數

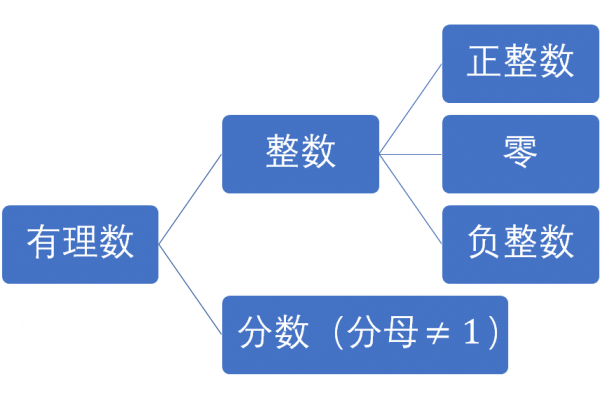
有理數，是整數和分數的統稱，而整數又可以分為正整數、負整數和零。

而整數總能寫成的形式，其中是整數（零可以寫成）。

因此有理數就是能夠化為兩個整數之比的數，有理數的希臘文為，原意為“成比例的數”，英文以ratio（比例）為詞根，在字尾加上-nal構成形容詞，全名為rational number，直譯成漢語應該是“可比數”。

那麼，為什麼如今我們學習的名稱不是“可比數”，而是“有理數”呢？這是由於數學知識在飄洋過海的過程中出現了“誤讀”，這是東西方數學文化傳播中的一個著名烏龍事件。

有理數這一概念最早源自西方《幾何原本》，在中國明代，從西方傳入中國，明末數學家徐光啟和學者利瑪竇翻譯《幾何原本》前6卷時的底本是拉丁文。他們將這個詞（）譯為“理”，這裡的“理”指的是它的本意“比值”。

徐光啟與利瑪竇

而日本在明治維新以前，歐美數學典籍的譯本多半採用中國文言文的譯本。因此日本學者將中國文言文中的“理”直接翻譯成了“道理”，而不是文言文所解釋的“比值”。後來，日本學者直接用錯誤的理解翻譯出了“有理數”和“無理數”。

在明治維新之後，日本的數學得到了迅猛的發展。到了清末，近代處於落後地位的中國不得不開始派遣留學生到日本進行學習，中國留學生又將錯誤傳回中國，大有“出口轉內銷”的意味，於是“有理數”以訛傳訛，沿用至今。

2 無理數

有理數聽起來就像是“有道理的數”，這個觀點若是放在古希臘時代可能會非常流行，特別是對於奉行“萬物皆數”，將（有理）數看作是宇宙萬物本源的畢達哥拉斯學派更是如此，他們認為所有事物的性質都是由數量關係決定的，萬物按照一定的數量比例而構成和諧的秩序。

畢達哥拉斯（約公元前580年~約公元前500年）

然而畢達哥拉斯的學生希帕索斯發現正方形對角線與邊長為不可公度量（即兩者的長度之比不能表達為整數之比），無理數的發現對畢達哥拉斯的哲學造成了毀滅性的打擊，發現了真理的希帕索斯被畢達哥拉斯學派的門徒們拋進大海處死。於是很多中學教師這樣告訴學生：希帕索斯因為發現無理數而失去生命，此事太沒有“道理”，所以他所發現的數被稱為“無理數”。

然而，這個傳說未必可信，畢達哥拉斯學派有許多嚴格且奇怪的規矩，比如“禁食豆子”，“東西落下了，不要用手揀起來”等等，最重要的是，在畢達哥拉斯建立的團體中，財產是公有的，而且學派的成員們有一種共同的生活方式，甚至於科學和數學的發現也被認為是集體的，所以更可能的情形是——希帕索斯因違反了畢達哥拉斯學派的規矩而被驅逐出學派。

因此認為無理數是“沒有道理的數”實際上是對其的誤解。同有理數一樣，無理數的命名也是源於翻譯問題。實際上，無理數的英文為irrational number，irrational的原意是“不可比的”或“不能表達成比率的”。所謂的“無理數”，不過是“無比數”的誤譯而已。