女士們,先生們,老少爺們兒們!在下張大少。
Rangolee是一種古老的印度地板裝飾藝術,建立在矩形或六邊形點陣上,作為基於自然/文化世界抽象的設計和圖案的基礎。在本文中,我們根據rangolee設計的創作方法和出現的動機對其進行分類。我們將這些傳統和當代設計與數學領域獨立出現的圖案和模型聯絡起來。這包括各種對稱群、螺旋、映象曲線、分形自相似和迭代過程。
印度大嬸的Rangolee藝術
Rangolee:“Rangolee”在印度語中稱為Marathi,意思是彩色線條:"rang "指顏色,"oralee "指線條。Rangolee是一種古老的地板裝飾藝術,用於歡迎客人、帶來新的季節、婚禮、生日等場合。Rangolee這個詞也被用來指用於繪製圖案的粉末。這種粉末可以透過碾碎火石或大米制成。在印度南部,最常使用的是米粉。
用拇指和食指夾住一撮粉末。滾動拇指,慢慢地將粉末釋放出來,形成一條細流。自由移動手,畫出點和線。這需要大量的手和眼的協調,就像最初繪製等距離的長方形或六邊形的點陣一樣,開始了繪製過程。
分類:有三種基本的繪畫方法,我們可以用這些方法對設計進行大致分類。
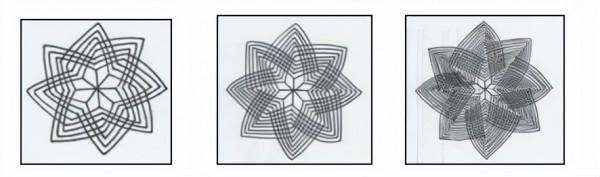
(a) 將點畫成矩形或等距格子的一部分,然後按照一定的順序連線起來,形成幾何形狀,或圖案,或自然物體,如水果、樹葉、花朵、動物或鳥。圖1a、1b、1c和1d就是這種形式。
(b)如(a)所示繪製點,並在點周圍繪製曲線,形成幾何圖案或自然物體。這些被稱為kolam。圖1e中的梵天結是kolam。
(c)徒手繪製幾何形狀的圖畫(圓形更常見,但也有正方形和三角形的形式)歷史、史詩或宇宙古史(傳統故事)中的自然物體或場景。一個對稱的頂篷可以圍繞著一個餐盤或木板,邀請客人、新婚夫婦或新媽媽坐在上面。

圖1a: 椰子 圖1b: Koyaree 圖 1c: Bilve patra 圖 1d: 海龜 圖1e: 梵天結
人們也可以將rangolee分為傳統設計和當代設計。
傳統設計:圖1a-1e和2a-2c中的傳統設計要麼具有特殊的文化意義,要麼具有宗教意義。簡而言之,koyaree代表芒果種子,saraswatee代表知識女神,nabhi kamal代表宇宙臍帶的蓮花,bilve patra代表Rutaceae(溼婆神的最愛)的葉片,dnyan kamal代表知識的蓮花。除此以外,還發現了太陽、月亮、卍字、牛蹄印和海螺的自由手繪。

圖2a:Saraswatee 圖2b:Nabhi Kama l圖2c:Dnayn Kamal 圖2d:當代
當代設計:當代設計要麼是用點畫的,要麼是徒手畫的。點被連線起來形成自然物體,如花、鳥、動物或幾何形狀,如圖2d所示。在rangolee中,人們更容易看到像玫瑰、芙蓉和蓮花這樣的花朵,或者像天鵝、鸚鵡和孔雀這樣的鳥類,或者像大象、魚或鹿這樣的動物。
在Rangolee設計中感受到的數學
因為它們本質上是基於晶格對稱性和從自然世界中抽象出形式的設計,所以在rangolee設計中我們可以從數學世界中找到各種形式和模型的表現也就不足為奇了。在這一節中,我們說明了一些我們已經能夠找到的形式:對稱性、分形、映象曲線、迴圈順序和迭代。
圖案:以六邊形陣列畫點,在垂直向上或向下移動時減少每一行的點的數量,這在傳統的rangolee 設計中是很常見的。有趣的是,從一組給定的點中,我們可以看到有多少種可能的方式來繪製一個圖案。一個由四個水平等距的點組成的基礎,在頂部和底部都減少為一個,可以連線起來形成封閉的圖案。在一個案例中,這創造了椰子的基本圖案,而在另一個案例中,一個小的菱形被嵌入一個較大的菱形中。椰子圖案很突出,因為它既有趣又漂亮。原因可能是所有的點都以某種方式相互連線。
分形:分形大約在30年前開始流行,儘管它們一直存在於自然界中,像謝爾賓斯基地毯這樣著名的分形可以追溯到近一個世紀。分形的一個共同來源是遞減的自相似性。我們可以在圖3a中感知到2級分形的自相似性,其中基本的十字架在三個尺度上重複。
映象曲線:Gerdes[4]將非洲的一些設計描述為m-canonical映象曲線。這些設計與kolam rangolee非常相似。其中的線條是尤拉路徑的例子,設計完成後不需要從表面提起鉛筆,也不需要回溯線條的任何部分。它們被稱為單線。其他的是雙線或三線。有三種映象曲線:簡單、規則和米字形。見圖3b和圖3c。

圖3:(a)葡萄藤 (b)簡單圖 (c)規則圖 (d)Saraswatee:前三次迭代
迴圈順序:
A.Dnyan kamal:有兩種方式連線點,產生相反形式的迴圈對稱,如圖2c所示。
1) 1到4,2到5,形成兩個順時針螺旋;3比1、4比2和5比3形成三個逆時針螺旋。這是最常見的連點方式;
2)連線1到3、2到4、3到5形成三個順時針螺旋;並且連線2比1和3比2以產生兩個逆時針螺旋。
Siromoney [2]將點連線的順序描述為(1,3,5,2,4,1)。重複這個模式8次後,dnyan kamal就完成了。這是一幅單線圖。
B.Saraswatee:圖3d顯示了用一根、兩根和三根手杖繪製的Saraswatee。手杖上的數字應該有助於理解連線它們的順序,如下所述。
用一根手杖連線的Saraswatee的順序是1到1
兩根手杖的順序是1到2,2到1
三根手杖的順序是1到3,2到2,3到1。
……
N根手杖的順序是1到N,2到N-1,...N-1到2,N到1
迭代:從基本圖案中製作更大的圖案是一項有趣的、具有挑戰性的活動。例如,我們在上面看到如何繪製椰子的基本圖案。我們可以在六邊形格子的八個點的基礎上進行迭代構建。進一步的迭代是基於十二個點。我們可以把這寫成遞迴的形式,其中點的數量由n(i+1) = n( i ) + 4給出。
複雜的迭代中的椰子圖案彼此之間沒有任何聯絡。而bilve patra在第一次和連續的迭代中,有一個或兩個點與下一個圖案相連。所有其他的圖案在連續的迭代中顯示出一個或多個線條或形狀的重疊。在椰子、烏龜、nabhi kamal和koyaree設計的第n次迭代中,人們還發現了(n+1)^2個基本圖案,這些圖案是基於六角形的點陣。見以下對圖4a和4b中例子的描述。
Koyaree迭代:Koyaree的基本圖案是先畫7個水平等距的點,然後從六邊形陣列中遞減行,直到我們在頂部和底部兩端各畫一個。下一次迭代從11個點開始,如圖4a所示。圖4b顯示了進一步迭代的koyaree,從15個點開始。你在第一次迭代中發現了四個基本圖案,在第二次迭代中發現了九個。
在繪製Dnyan Kamal的迭代圖時,我們希望保持圖紙中的單線性,因為它允許編寫高效的計算機程式來在計算機的幫助下建立設計。圖4c、4d和4e分別顯示了具有8、13和21個點的圖。儘管看起來很漂亮,圖4C中的8個點並不是單線的。圖4c將透過以下數字模式(1,4,7,2,5,8,3,6,1)8次顯示5個順時針和3個逆時針螺旋來完成。圖4d將透過以下數字模式(1,6,11,3,8,13,5,10,2,7,12,4,9,1)8次顯示8個順時針和5個逆時針螺旋來完成。迭代也是用不同的臂數繪製的。例如,花瓣可以是4、6、12、16……而不是8個。
計算機科學:印度金奈基督教學院的SiroMoney[2]和美國伊薩卡學院的Ascher[3]廣泛研究了隱藏在dnyan Kamal、葡萄藤、Koyaree和其他kolam設計中的邏輯和遞迴語言。最近在對kolam設計的分析中發現了更多的內容[4]。
參考文獻
[1] P. Gerdes, Geometry from Africa: Mathematical and Educational Explorations. Washington, D.C.: Mathematical Association of America. 1999.
[2] G. Siromoney, Kolam, Kavyashastra Quarterly, April 1978. http://www.cmi.ac.in/gift/Kolam.htm
[3] M. Ascher, The Kolam Tradition; American Scientist, 2003.
[4] Y. Kawai, K. Takhashi, S. Nagata, PsyKolo3D-Interactive Computer Graphical Content of “Kolam” Design Blocks. Forma, Vol. 22, pp.113-118, 2007
[5] Madhuri Bapat, Mathematics in Rangolee Art from India
青山不改,綠水長流,在下告退。
轉發隨意,轉載請聯絡張大少本尊。