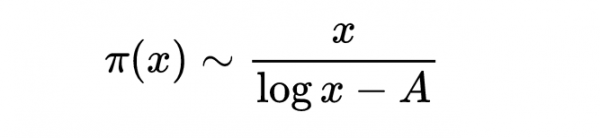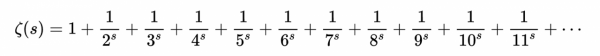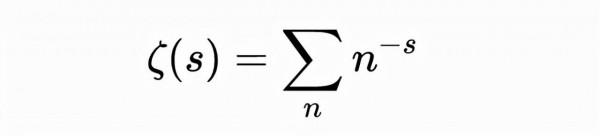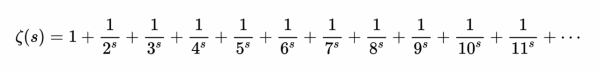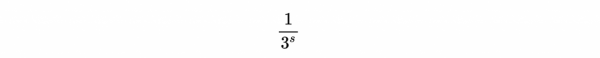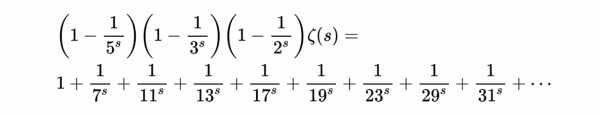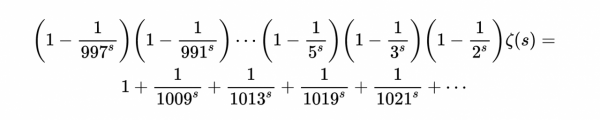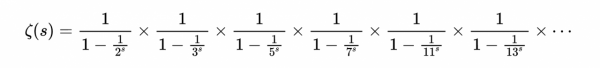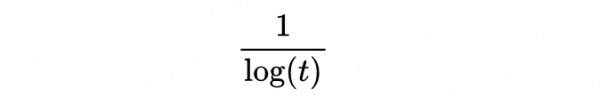用最簡單的方式解釋黎曼猜想（二），黎曼ζ函式，素數的金鑰匙

高斯對素數的研究‍

第一個發現素數定理（PNT）真理的人是卡爾·弗里德里希·高斯。高斯是有史以來最偉大的數學家之一。他被稱為“數學王子”。1849年12月，高斯與天文學家約翰·弗朗茨·恩克通訊說：

你對質數頻率的說法使我感興趣，這讓我想起了我自己對這一主題的研究，在1792年或1793年，我將我的注意力集中到質數頻率的降低上……我很快意識到，這個頻率，平均來說，與對數近似成反比。

高斯計算的是1000個連續整數中有多少個質數，從1792年開始（那時他才15歲），高斯把所有質數以1000個數字為單位一次計數，一直到幾十萬（還沒算到一百萬），以此作為消遣。

1798年，也就是高斯發現PNT的幾年之後，勒讓德出版了一本名為《論數論》的書，在書中，他推測：

在這本書的最後一個版本中，他對這個猜想進行了改進：

其中，當x較大時，A趨於1.08366附近的某一數值。高斯在1849年寫給恩克的信中討論了勒讓德的猜想。他否定了1.08366的值，但沒有得出其他非常明確的結論。

巴賽爾問題‍

巴塞爾問題要求的是自然數平方和的倒數的精確和，即無窮級數的精確和：

巴塞爾問題的名字來源於一座瑞士城市，伯努利兄弟曾先後在這座大學擔任數學教授二人都證明了調和級數（所有自然數倒數之和）是發現的。雅各布·伯努利陳述了上述問題（巴賽爾問題）。

我們知道調和級數發散非常“勉強”，前10^43項之和仍不超過100！而巴塞爾級數中的每一項都小於調和級數中的對應項。因此，我們猜測巴賽爾級數應該是收斂的。

計算表明確實如此。巴賽爾級數前10之和為1.5497677，前100項之和為1.6349839，前1000項之和是1.6439345，前10000項之和是1.6448340。它確實收斂到1.644或1.645附近的某個數值。但那個收斂值具體是多少？

這個問題終於在1735年被年輕的尤拉解開。令人吃驚的答案是：

答案包含了我們熟悉的圓周率π。這在當時讓數學家們感到非常吃驚。

巴塞爾問題打開了zeta函式的大門，這是黎曼猜想所關注的數學物件。巴塞爾問題的尤拉解不僅給出了平方倒數級數的閉形式，它還把N推廣到了整個偶數範圍：

當N=2時，級數收斂到（π^2）/6（這也是兩個自然數互質的機率，很神奇是不是）。N=4時，收斂值為（π^4）/90；N=6時，收斂值是（π^6）/945。尤拉自己一直把N算到了26，結果是：

但如果N是奇數呢？尤拉的結果與奇數無關。此後的260多年時間裡，數學家都不知道N為奇數時的收斂值如：

沒有人能夠找到這些級數的封閉形式，我們只知道它們確實是收斂的。直到1978年才證明N=3時，級數收斂值是無理數。到18世紀中葉，很多數學家都在思考無窮級數如下表1：

N	收斂值
1	發散
2	1.644934066848
3	1.202056903159
4	1.082323233711
5	1.036927755143
6	1.017343061984

表1

表1是對黎曼ζ函式的初步瞭解，這是理解黎曼猜想的第一步。

為了紀念這個新的認識，我將把“N”換成一個不同的字母，一個與整數沒有那麼聯絡的字母。當然，顯而易見的選擇是“x”。然而，黎曼本人在1859年的論文中並沒有使用“x”，他用的是“s”。最後，是黎曼zeta函式形式是：

用求和符號表示為：

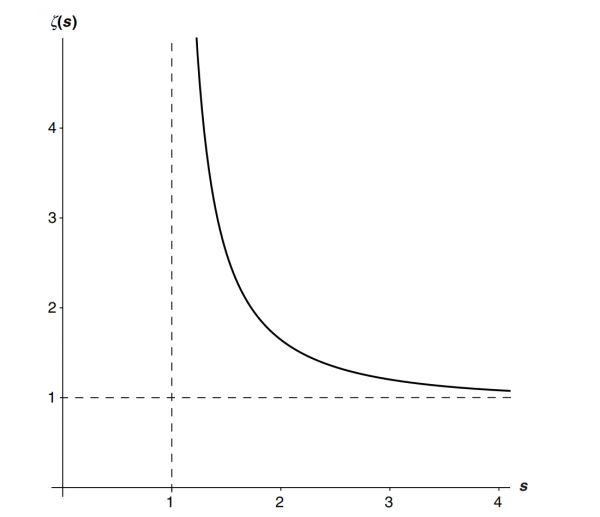
讓我們把注意力轉向引數s，當s = 1時，級數發散，因此函式沒有值。當s為2，3，4時，它總是收斂的。事實上，可以證明這個級數對任何s大於1的數都是收斂的。當s為1.5時，收斂到2.612375；當s為1.1時，收斂到10.584448.；當s為1.0001時，它收斂於100000.577222。當s = 1時級數發散，但當s = 1.0001時級數卻收斂，這似乎很奇怪。

畫出函式圖更能說明情況。下面是zeta函式的曲線圖。

可以看到，當s從右邊接近1時，函式值上升到無窮大；當s在最右邊趨於無窮時，函式值越來越接近於1。如果s=0呢？

根據冪法則4，這個和是1 + 1 + 1 + 1 + 1 + 1 + 1 +…，它很明顯是發散的。

對於負數，情況更糟。由冪法則5，知道2^（-1）=1/2，3^（-1）=1/3……而1/（1/2）=2，1/（1/3）=3……因此，s=-1時，級數是1+2+3+4+5……顯然是發散的。如果s=1/2呢？由於2^（1/2）=sqrt（2），因此：

因為任何整數的平方根都比這個數小，所以這個級數中的每一項都比調和級數中相應的項大，因此它是發散的。

上圖似乎顯示了黎曼zeta函式的所有特徵。函式只有當s大於1時才有值。或者，正如我們現在所知道的，用恰當的術語來說，函式的定義域是所有大於1的數。對吧？錯了！

埃拉托色尼篩選法‍

埃拉托色尼是亞歷山大大圖書館的圖書管理員之一。他提出了著名的尋找質數的方法。原理是這樣的：首先，寫下所有的整數，從2開始。當然，你不可能把它們都寫下來，所以我們就用100個左右吧：

現在，保持2不變，剔除數表中所有2的倍數的數，得到：

2之後的第一個數字是3。保持2、3不變，剔除數表中所有3的倍數的數，得到：

3之後第一個未受影響的數字是5。保持2、3和5不變，剔除數表中所有5的倍數的數，得到：

第一個未受影響的數字是7。下一步是讓2、3、5、7保持不變，剔除數表中所有7的倍數的數，以此類推，最後剩下的數就是質數。這就是埃拉托色尼篩選法。

Tip：

埃拉托色尼的篩選法很簡單，已有2230年的歷史。它是如何讓我們進入19世紀中期，並對函數理論產生深遠影響的？

黎曼ζ函式‍

這一次，我將把它應用到黎曼ζ函式上，我在上面定義了黎曼函式，函式只有當s大於1時才有值。

表示式1

注意，這樣寫需要寫出所有的正整數，這與埃拉托色尼的篩選法有什麼聯絡？我要做的是在等號兩邊同時乘以：

得到：

表示式2

現在，我用表示式1減去表示式2，得到：

這消除了所有的偶數項，只剩下奇數項。

回顧下埃拉托色尼篩選法，我現在要在等號兩邊同時乘以：

3是右邊第一個沒受影響的數字。

表示式3

現在用表示式2減去表示式3，得到：

所有3的倍數都消失了。右邊第一個數字變成了5。繼續下去得到：

注意到和埃拉托色尼篩選法相似了嗎？實際上，你應該首先注意到區別。在埃拉托色尼篩選法中，我讓以此讓2、3、5、7……保持不變，依次剔除它們的整數倍。而現在，我從右邊刪除了原始質數（2、3、5、7……）以及它的所有倍數。

如果我一直下去直到一個較大的質數，比如997，得到：

表示式4

右邊，如果s是任何大於1的數，那右邊就比1稍大一點。例如，如果s為3，則得到1.00000006731036081534。所以說，如果一直重複這個過程，會得到如下結果：

依次將上式兩邊重複地除以每個括號內的“東西”，得到：

這就是開啟質數大門的“金鑰匙”。為了展示它的優雅，讓我把它整理一下。我和你一樣不喜歡帶有分數分母的分數。用一點代數知識，整理得到：

表示式5

這又一次證明了質數有無窮多個。你可能會想，表示式5有什麼特別之處，或有什麼意義？這個問題的答案要到黎曼猜想系列文章的最後才能清楚。表示式5有個名字，叫“尤拉乘積公式”。

一個重要的函式‍‍

首先，考慮函式：

具體如圖1所示。我把變數x的符號換成了t。

圖1

我在圖中加了陰影，因為我要做一點積分。積分是一種計算函式下面積的方法。首先求出函式的積分。1 / log t的積分是多少？

不幸的是，沒有普通的函式可以用來表示1 / log t的積分。但這個積分又是非常重要的，它在我們對黎曼假設的研究中經常出現。數學家不想每次提到這個積分都寫一次下面的表示式：

因此，數學家給它一個名字叫“log積分函式”，通常用“Li（x）”表示，有時也用“li（x）”。求這個函式值（也就是陰影面積）需要一定的技巧，因為1 ⁄ log t在t=1時沒有值。我將輕鬆地克服這個小困難。只需要注意的是，當計算積分時，水平軸以下的面積被認為是負的，因此隨著t的增加，1右邊的面積抵消了左邊的面積。

下圖2是Li（x）的函式圖。

圖2

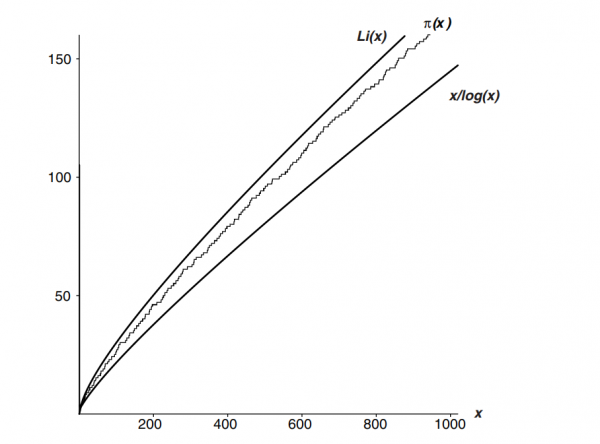
注意，當x<1時，它是負的。它在x = 1時向負無窮下降，但隨著x向1右側移動，正的面積逐漸抵消負的，使Li(x)從負無窮返回，在x = 1.4513692348828處達到0。此後穩步增長。它在任意點的梯度，當然是1 / log x。此外，回顧一下我上篇文章，一個整數在x的附近是質數的機率是？

這就是為什麼這個函式在數論中如此重要。你看，隨著N變大，Li(N) ~ N / log N。現在根據素數定理， π (N) ~ N ⁄ log N。我們知道這個小波浪號“~”是可傳遞的。如果P ~ Q並且Q ~ R，那麼P ~ R。因此，如果素數定理是正確的（確實正確，在1896年得證），那麼也一定有 π (N) ~ Li(N)。

Li(N)實際上是π (N)比N / log N更好的估近似。