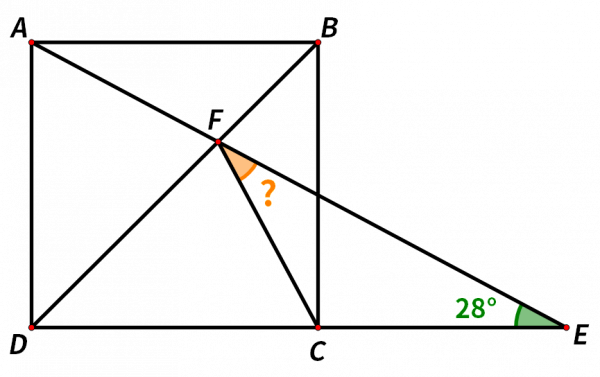
如圖,四邊形ABCD是正方形,延長DC到點E,連線AE,AE和BD交於點F,連線CF,∠E=28°,求∠CFE的度數。這道題怎麼做呢?
這道題只是看起來有些複雜,實際上就是隻紙老虎。
根據題目條件,我們很容易得到三角形ADF和三角形CDF全等。為什麼?
在三角形ADF和三角形CDF中,
AD=CD(正方形ABCD的邊長相等),
∠ADB=∠CDB=45°(正方形ABCD的對角線BD平分正方形的內角),
DF=DF(公共邊),
由邊角邊證全等,可得三角形ADF和三角形CDF全等。
三角形ADF和三角形CDF全等,∠DAF=∠DCF。
而在直到三角形ADE中,∠DAF和∠E互餘,∠DAF+∠E=90°,∠E=28°,所以∠DAF =62°,
∠DCF=∠DAF =62°。
根據三角形的外角會等於不相鄰的兩個內角之和,又可以得到∠DCF=∠CFE+∠E,
∠DCF=62°,∠E=28°,
所以∠CFE =∠DCF-∠E =62°-28°=34°。
以上就是這道題的解法,除此之外你還有其他方法嗎?可以在評論區留言~