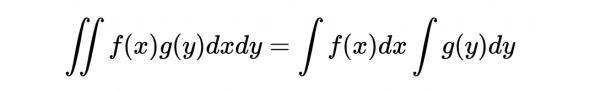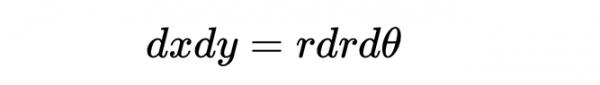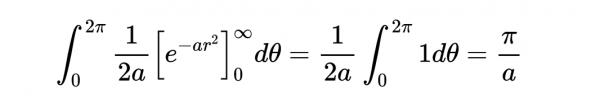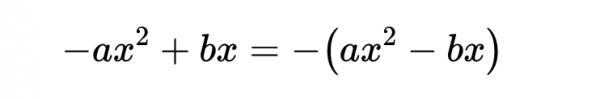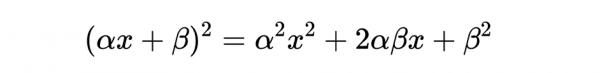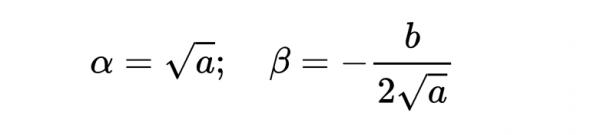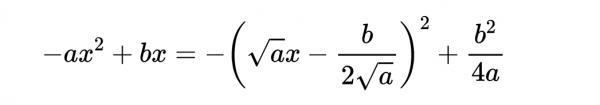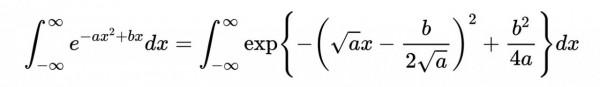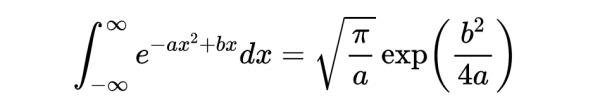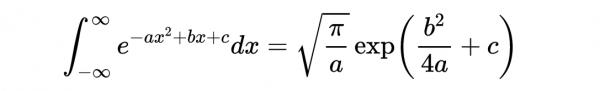高斯積分在科學、統計學和機率論中經常出現。事實上，如果熟悉統計學中的正態分佈（也被稱為 "貝爾曲線"），那麼你可能知道什麼是高斯函式。

高斯積分本質上是高斯函式下的面積。本文將研究高斯函式下的總面積是多少，這意味著我們將計算一個無限域的積分，並將這個結果應用於高斯函式的多種變化。

最簡單的高斯積分的形式是：

• 式1：高斯積分結果

引數a用來控制高斯分佈的 "寬窄 "程度。高斯分佈的中心是x = 0，它有以下特性：a越小，高斯分佈越“寬”，a越大，高斯分佈越 "窄"。從這個結果來看，比較令人驚訝的是，總面積是：

我們也許會猜想它與a成反比，因為高斯分佈的寬度會影響面積，但是為什麼π會出現在這裡呢？為了弄清楚這個問題，我們將從二維的角度來處理這個問題。

一個技巧：轉換為極座標

首先，讓我們把積分寫成：

我們也可以用不同的變數來表示，比如用y：

將兩者相乘，我們可以得到：

這裡我們可以做一個簡化處理。首先，我們注意到，根據福比尼的積分定理（Fubini’s theorem of integration），如果一個雙積分有常數（或與變數無關的）極限，我們可以將兩個積分的乘積合併為一個雙積分，即：

在這個的例子中是：

現在，看一下指數項，我們注意到有平方和。根據勾股定理，們可以將另一個變數寫為：

其中r是三角形的斜邊。在極座標下，r是圓的半徑。同樣地，我們可以定義一個相對於正X軸的角度。利用這兩個新變數，我們可以對積分進行變換。然而，這還不夠。積分的極限肯定會改變，因為在笛卡爾座標系中，積分的定義域是一個長為無窮大的矩形邊（因為在x和y上從負無窮到正無窮積分），在極座標中會是什麼樣子？

那麼，肯定也會有一個無限的域。然而，有一些限制：半徑r根據定義被限制在[0,∞]內，因為半徑不能是負的。其次，角度被限制在[0,2π]。因此，極座標下的積分是不同的。

另外需要注意的是，從直角座標轉換為極座標時，無窮小的增量dx和dy也將發生變化。事實上，由於兩者的乘積是一個 "無限小的矩形區域"，當我們將這個矩形轉換為極座標時，我們應該得到：

其中d是一個無窮小的弧長，dr是半徑方向的無窮小變化。將所有這些結合起來，我們的積分就變成了：

這裡，我們可以用換元法求解內積分：

得到：

這就是I^2的值，所以現在為了得到我們想要的積分值，我們只需取兩邊的平方根，從而得到所需的結果：

擴充套件

我們還可以用不同的形式來研究高斯積分。例如，考慮：

這稍微有點複雜，但我們可以這樣來求解：

也可以把它寫成：

其中：

得到：

因此：

這裡，我們可以做一個替換：

這樣：

利用公式1的結果：

因此，結果是：

• 方程2：形式為ax^2+bx的高斯積分

有趣的是，同樣的過程也可以用於得到下面的結果：

• 方程3：形式為ax^2+bx+c的高斯積分

如前所述，高斯積分有多種用途。其中最常見的是在統計學中的正態分佈中，實際上一個連續隨機變數X的點的分佈是高斯分佈：X的大多數隨機樣本將落在均值E[X]附近，方差Var[X]決定高斯分佈的寬度或狹窄程度。因此，Var[X]越大，點的分佈越廣。