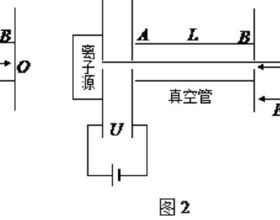
運動的週期性是形成多解問題最難的也是最常考的一個因素。帶電粒子在部分是電場、部分是磁場的空間運動時,運動往往具有往復性,從而形成多解。如圖所示.
強調的是,構造週期性問題的方法很多,角度也很多樣,特別是從題目表面根本無法識別它是否是考察週期性問題。這就需要我們分析問題的時候時刻緊繃多解這根弦。
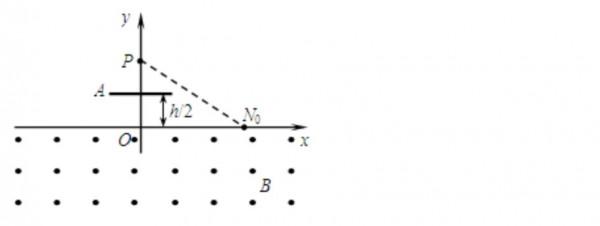
還是拿一道例題說明。如圖,在x軸下方有勻強磁場,磁感應強度大小為B,方向垂直於x y平面向外。P是y軸上距原點為h的一點,N 0 為x軸上距原點為a的一點。A是一塊平行於x軸的擋板,與x軸的距離為 h 2 ,A的中點在y軸上,長度略小於 a /2 。帶電粒子與擋板碰撞前後,x方向的分速度不變,y方向的分速度反向、大小不變。質量為m,電荷量為q(q>0)的粒子從P點瞄準N 0 點入射,最後又透過P點.不計重力.
(1)若粒子從P點射出的速率為v,求粒子在磁場中運動的軌道半徑R;
(2)求粒子從N 0 點射入磁場到第一次穿出磁場所經歷的時間.(可用反三角函式表示)
(3)求粒子入射速度的所有可能值。
解析:這是一道非常經典的高考壓軸題,它的難度在當時乃至現在來說都是比較難的。而今天我們就來試圖用程式化的方法看能否快速解決或者快速拿到足夠多的分數。
第一問如果你告訴我不會,那我真的無語了。不再贅述,半徑R=mv/qB。
第二問時間。兩個方法,顯然本題只能用其中一個。總之,只要知道速度偏轉角或者速度與位移方向的夾角或者軌跡圓對應的圓周角,問題就可以解決。入射速度方向與位移方向的夾角θ在直角三角形PN0O中非常容易就可以得到。不再贅述。應該說前兩問沒有什麼難度,但有的小夥伴心理素質不好造成失分,實屬可惜。
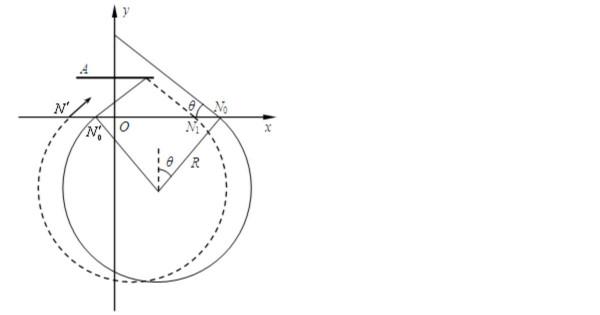
第三問就是精華所在,如果你碰到類似的問題不會,怎麼辦?稍微動一點聰明的大腦,就可以發現不碰擋板有可能過P點,此時的速度是一個可能值吧?答上這個答案,又拿到了一部分分數。如果要衝刺高分,那麼既然說碰擋板如何如何,那麼畫圖的時候我們就先讓它碰到最右端,看會怎樣。如圖所示。動態圓中的平移、單邊界磁場區域的偏移、擊中P點需要滿足條件中的對稱,種種我們以前談到的知識點綜合在一起就構成了此題的難點。網上關於本題的處理方法有很多,但是我認為均不是很調理。我提供一種思路。透過畫圖和一定的分析可知,要想擊中P點,入射點和最終的出射點距離一定是2a。所以我們就算這個距離如何實現。碰撞一次這個距離應該是2Rsinθ-h/2/tanθ*2+2Rsinθ,那麼碰撞n次呢,這個距離應該是(2Rsinθ-h/2/tanθ*2)*n+2Rsinθ=2a,說白了每碰撞一次入射點和出射點的距離在2Rsinθ的基礎上增加一個偏移量。先看一個週期,再看次數影響什麼,最後寫等式,三步搞定。具體的數學運算或者次數的選取就給你留下了[耶]
結論:週期性問題的關鍵是找到什麼是週期,這個需要大家體會。
如果你有今日頭條app,麻煩順手點一下關注@中學物理知識傳播者,每天都會傾情奉獻一段小乾貨,我會繼續努力的!