我們知道數有很多分類,其中很重要的一點就是無理數。
π是我們最早認識到無理數,另外在解方程的時候,我們發現了了開方運算,就出現了無理數。
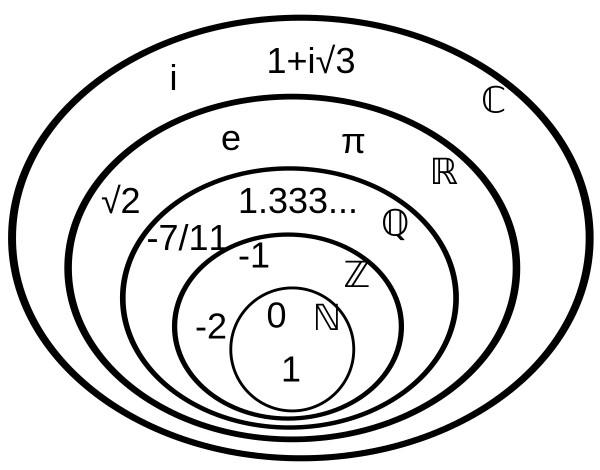
數的認識逐漸形成了以下的分類。
0、正整數與負整數,小數與整數,負數與正數,實數與虛數,有理數與無理數,對數與指數。另外還有一種多維數,可以有無數個維度組成的數。不過由於虛數的關係,我們的多維數研究基本停留在了二維的虛數環節。
由於我要發展多維空間理論,要找到一些數學依據,所以我對多維數好好進行了深入思考。
我發現多維數對於我們認識和理解事物有很大的幫助,對於進一步研究數也是非常有意義的。
比如通常情況下我們認為一條數軸,就能包括所有的實數。但是我們不清楚無理數,之所以會是無理數,是因為這些無理數是多維數在一維空間中的數值。
比如根號二,在二維空間中根號二可以表示成(1,1)到(0,0)的距離。我們可以將二維點到原點的距離定義為/1,1/(可以用其他方式表示,就是用新的符合去表示),這樣根號二就有了二維空間中的精確數值。
同樣我們可以將所有有理數的開多次方,放到多維空間中,找到一個點,用//的方式將開方的無理數表示為多維空間中的數。
不過多維空間中的點到原點距離有很多個,比如根號二在二維空間中,這個點是一個圓環。在圓環上的所有點到原點的距離都是根號二。圓環上也有很多無理數,不過很多也是有理數。
多維數對於我們解決問題有很多好處,其中一個就是那可以是精確值。不過數之間的計算我們現在基本上是停留在一個維度上,所以多維數都需要轉化為一維數。
我覺得很多時候可以用多個維度的有理數去計算這樣會更加準確。
我們可以知道物理是有一個叫做粒子性,物體總是一份一份的。這說明了什麼呢?物體的粒子性,代表一種有理性,而不是如同無理數一樣小數永遠計算不玩。
無理數的小數之所以一直永遠計算不完,是因為我們將二維數變化成了一維數,兩個維度構成的數,要放在一個維度,就是無法斬斷另外一個維度的影響,另外一個維度永遠會影響一維,這就是一種垂直關係的間接影響。
無理數數的無理性就是一種多維空間的間接影響。
我們知道相互垂直方向,不能產生相互作用力,但是會形成空間維度的間接作用。我猜測正式這樣空間維度的間接作用導致了萬有引力的產生。
我們知道萬有引力定律有一個常數G,我猜猜這個常數G就是由於空間維度的間接影響帶來的。也就是說,可能常數G就是其他維度在多維空間對三維空間的間接影響。物體之間的關係的根本是一種多維空間中的相互作用。
比如地球與太陽之間是一種多維空間中的相互作用,最終形成了現在的現象。生活中有很多數,這些數可以說就是分佈在多維空間中的數。要進行一些計算,其中一個方法就是在每個維度進行各自維度的計算,這樣認識起來會更加清楚,一目瞭然。如果我們將一些多維數轉化為一維數去計算,那麼將會更加複雜。
比如多元一次方程,x+y+z=1如果我們要這麼去解答方程就不太容易,如果我們能在三維空間中去看,這個方程就有更加明確的認識。一個三元方程沒有唯一解,如果要有確定的解,就需要三個三元方程。
如果我們畫出三維影象就可以更加明確這些解到底是怎麼回事。
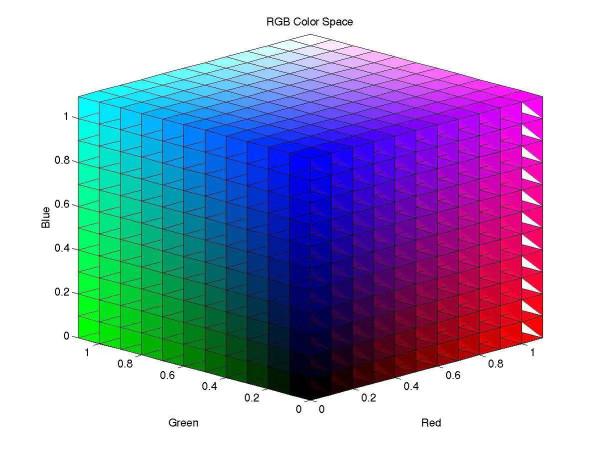
另外四維影象也是能畫出來的。我們可以用顏色代表一個維度來畫。五維也是能畫出來的。我們可以增加一個時間維度,得到一個動態的影象。
在增加時間維度之後,更多的維度都是能畫出來的。我們可以用不同形狀代表不同的維度變化。很多三維空間中看到的形狀變化也就是物體在多維空間中運動變化的間接影響,或者說說一種對映。
我們很多時候將形狀在三維空間中就以為是三維空間的。這是一種三維世界觀造成的。
三維世界觀導致了我們無法解決很多問題,無法解釋很多問題。
多維空間理論能更好去解決很多實際問題,看清楚以前一直無法看清楚的很多問題。
要認識多維空間應該從多維數開始,多維空間中的計算應該更多地從各個空間維度去計算。
未來必然需要一種多維空間中的計算,透過多維空間理論的發展也會發展出新的計算機。這樣的計算機計算效率將大大提高。
歡迎大家多多關注沙漠月亮灣,我將帶大家進入多維空間世界!