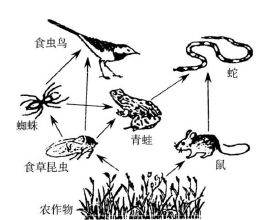
從數學角度分析全民核酸檢測
對於病毒群體檢測而言,區塊與群在特定時候是可以互動的。
今天是清明時節,春和景明,我們寄託哀思。為快速徹底阻斷疫情發生,提高精準防控的效率,全國各地都在做全民核酸檢測。那麼從核酸檢測中就抽象出一個數學問題-區塊測試,每次測多少樣本是最佳標準呢?
在有近2年來抗疫經歷後,獲得的實際經驗,需全面跟蹤確診者(陽性患者)包括無症狀感染者及確診者的(次)密接者。但是,這跟蹤檢測精準防疫經驗要真正實施,需保證核酸檢測率得跟上。美國在前總統的拖延下,錯過最佳時機,後來檢測跟不上,不得已選擇“躺平”。在現有情況下,提高檢測效率就成了當務之急。
根據群檢方法,每次把5個人或10個人的取樣先部分混檢,如果是陰性,則大家全部陰性;如果混檢是陽性,再進行每人單獨分測。這個初衷很好,但操作有些許麻煩。採用這種方法要想達到真實高效,重點的前提是必須滿足假設很低的陽性率,即當地社會面已幾乎全部清零。而若陽性率大於0.2,就幾乎不划算了,也會造成社會基層民眾的負面感。
當前,我們國家醫療水平已大體解決了取樣操作問題,現在我們單純從效率來考慮問題。
假設基於給定一個已知的陽性率0.1,每次檢測多少樣本(樣本容量)才能達到最大效率。疫情初前期,有專家(含國外)建議是每次5個,但是在陽性率是0.1的情況下,5個是最好的選擇嗎?
在回答這個題目之前,我們先來看經典的找次品問題。
有一批零件裡有一些分量不足的次品,次品率是1%,也就是說平均每100個零件裡有一個次品(分量不足)。現在讓你用秤來找出這些次品。怎樣秤效率最高?(假設你已經有很多標準零件)。
現比如,假設有100個零件。一個一個地秤,需要秤100次。每次進行兩個地秤,需要先秤50次。如果有些組發現有次品,還需對有次品的那些組每一個再秤一次。如果次品率是1%的話,50組裡平均有一組會有次品,也就是說還得再秤兩次,總共52次,這樣的秤法立馬就幾乎把效率提高了一倍。當然,兩次不是最佳選擇,多少次是最佳選擇呢?
我們把這個問題一般化,假設次品率是p,每次秤m個,這樣平均需要秤幾次?用統計學語言來表達,系需要計算檢測次數的期望值。
期望值的演算法是把每一種可能發生的情況的機率乘以其所對應的數值,然後加起來求和。
現比如:你花3塊錢去買彩票。為了增加變數,你買了三張不同種類的彩票。第一張獎額是10塊,中獎率是1/20;第二張獎額是100塊,中獎率是1/300;第三張獎額是10000塊,中獎率是1/60000。那麼,三張彩票你期望得到的錢是10•1/20 + 100•1/300 + 10000•1/60000 = 1/2+1/3+1/6 = 1。你花三塊錢買了一個1塊錢的期望值,另外兩塊錢交了智商稅。一般來說買彩票的人都是買同一種彩票,期望值演算法更簡單,而交智商稅的本質是一樣的,即以小獲多。
把這個期望值演算法應用到我們這個題目。一次秤m個零件,全都正常的機率是(1-p)^m,這種情況全過關,只需秤一次。有問題零件的機率是 1-(1-p)^m,這種情況,必須每個再秤,多秤m次,總共m+1 次。
數學期望值是:
E(x)=(1-p)^m + (1 - (1-p)^m)•(m+1) = 1 +(1 -(1-p)^m)•m
計算效率,把這個期望值除以m(逐個地秤需要m次)。如果商小於1,說明效率提高了。如果商大於1,說明效率降低了。要求最大效率,就是要求這個商的最小值。
上面的等式除以m得到期望效率為:
1/m + 1-(1-p)^m
在微積分學中,導數為0時會出現極值。所以,問題變成求導函式的零點。上面式子對m的導數是:
-1/m^2 - (1-p)^m • log(1-p) = 0
因為有對數和指數,它的零點(原函式的極值)很難求得。可以用數學軟體進行數值逼近。
考慮到通常 p 的值很小,我們可以透過近似方法直接進行運算求解。
由極限思想,把上面的期望效率展開為p的多項式並近可以省略高階項,我們得到 1/m +m•p , 對這個式子求導解極值就很容易了。
p - 1/m^2 = 0 ==> m = 1/sqrt(p)。這個雖然是近似值,但因為結果很漂亮,簡單好記,是粗估最佳解的好公式。比如,當 p = 1% 時,最佳解大概是10。
下圖是根據不同的p 值算出的最大效率 m值。藍線是精確解,紅線是近似解。可以看出,因為省略了高階項,近似解比精確解略小,但十分接近。把近似解朝上取整就與精確解相近。
橫座標-次品率
回到病毒檢測問題,從數學角度來說,與找次品零件是完全相同的問題。不過,實際操作起來,病毒檢測的生物操作要複雜的多。而且還要考慮時間成本。有些核酸檢測方法需要1天以後看結果,群測需要再測的話就要等2-3天,導致疫情雪上加霜。所以,群測問題還要考慮到隨之引起的操作複雜度及高度降低容錯率,出錯率的增加以及其它問題。
從上已知,如果陽性率超過0.2,最佳群測個數已經要小於3了。其提高的效率與增加的複雜性就需要一個權衡。單純從數字上來說,專家建議的5人一組,需要陽性率在0.5左右才是最優解。最新資料表明全美檢測的陽性率接近25%,韓國陽性患者已接近30%,一直保持高位執行。對於這麼高的陽性率,這個群測方法的實際意義就需要再三考慮了。
現我們具體實際情境化:
某大型社群為了切實保障居民的健康安全,貫徹好疫情期間衛生防疫工作的相關要求,決定在全社群範圍內舉行一次NCP普查,為此需要抽驗10000人的血樣進行化驗,由於人數較多,檢疫部門制訂了下列兩種可供選擇的方案.
方案①:將每個人的血分別化驗,這時需要驗10000次.
方案②:按k個人一組進行隨機分組,把從每組k個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這k個人的血只需檢驗一次( 這時認為每個人的血化驗1/k次);否則,若呈陽性,則需對這k個人的血樣再分別進行一次化驗,這樣,該組k個人的血總共需要化驗(k+1)次。
假設此次NCP普查中每個人的血樣化驗呈陽性的機率為p,且這些人之間的實驗反應相互獨立。
(1)設方案②中,某組k個人的每個人的血化驗次數為X,求X的分佈列;
(2)設p=0.1,試比較方案②中,k分別取2,3,4時,各需化驗的平均總次數;
並指出在這三種分組情況下,相比方案①,化驗次數最多可以平均減少多少次?(最後結果四捨五入保留整數)
解: 設每個人的血呈陰性反應的機率為q,則q=1-p,
所以:k個人的血混合後呈陰性反應的機率為qk,
呈陽性反應的機率為1-qk.
依題意可知X=k(1),1+k(1),
所以X的分佈列為:
|
X |
k(1) |
1+k(1) |
|
P |
qk |
1-qk |
在方案②中,結合(1)知每個人的平均化驗次數為:
E(X)=k(1)·qk + k(1)·(1-qk)=k(1)-qk+1 ,
k=2時,E(X)=2(1)-0.92+1≈0.69,此時10000人需要化驗的總次數為6900;
k=3時,E(X)=3(1)-0.93+1≈0.6043,此時10000人需要化驗的總次數為6043;
k=4時,E(X)=4(1)-0.94+1=0.5939,此時10000人需要化驗的總次數為5939,
即k=2時化驗次數最多,k=3時次數居中,k=4時化驗次數最少,
而採用方案①需化驗10000次(全都化驗),
故在這三種分組情況下,相比方案①:
需化驗次數最多可以平均減少10000-5939=4061次。
我們現在迎來好訊息,即新的更簡便、更快的補充檢測方法-抗原檢測試劑盒已經問世,可以大大提高檢測效率避免交叉感染。
現在從國家層面全民守“滬”,堅持動態清零目標不動搖,大機率是4月中旬全國絕大部分地區回到年初的正常生活水平。
讀書使人思想,思想使人領悟,領悟使人寬廣,寬廣才能承載。延古至今凡引領者,必善讀書、善思想、善領悟,胸懷寬廣承載萬千。