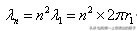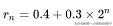新發現：核外電子軌道分佈與行星軌道分佈規律具有一致性！
核外電子軌道分佈
在半經典量子理論中，多電子原子中的電子軌道分佈遵循玻爾的軌道能級理論，即核外電子能級軌道半徑分佈規律為：
如果將原子核外電子分佈軌道半徑規律改寫成以軌道周長λ來描述的形式，則有：
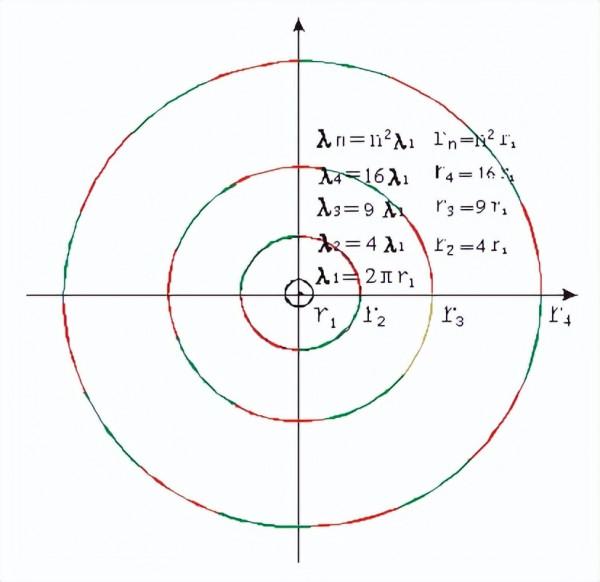
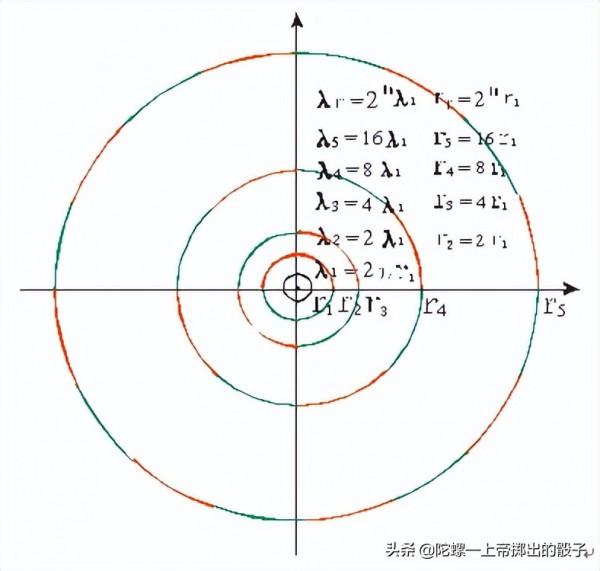
可見，不同穩定軌道周長之間按n=n²×r1規律拓展的本意是，電子第一軌道周長是λ1=2πr1，第二軌道周長就是第一軌道周長的4倍，即λ2=4×2πr1，第三軌道周長就是第一軌道周長的9倍，即λ3=9×2πr1……以此類推，第n軌道周長就是第一軌道周長的n²倍，即λn=n×2πr1，n∈[1、2、3、4…….]，現將這種軌道周長按n²倍式拓展形式繪成圖，如圖-1所示。
圖-1 . n^2 軌道拓展形式
我們從圖-1中還可以看出，玻爾電子穩定軌道周長按第一軌道周長n²倍拓展時，軌道周長拓展倍數不完全具有對稱，即有奇數不對稱情況出現，這就違反了埃米·諾特對稱與守恆及拉格朗日最小作用量原理，這種不具有完全對稱性的根源來自於玻爾的軌道角動量量子化假設條件，即他將電子核外軌道角動量規定為L=nh/2π後，其軌道周長拓展必然就不全具有對稱性，即存在奇數軌道周長拓展的形式，這也是半經典量子力學存在侷限性的原因之一。
核外電子運動
我們知道，現代原子模型起源於盧瑟福的原子行星結構模型，也就是說太陽系行星分佈模型與原子核外電子分佈有相通之處，但現行物理理論認為，行星在太陽系中的分佈規律與原子的電子分佈規律不同的，這是為什麼？難到真的是不一樣？
行星軌道分佈
早在1766年德國的一位中學教師戴維·提丟斯（Johann Daniel Titius，1729~1796）發現了一個關於太陽系中行星軌道分佈的簡單幾何分佈規則，即Ｒ＝ａ＋ｂc^n ；後來柏林天文臺的臺長波得（Johann Elert Bode）歸納成了一個經驗公式來表示，即
式中Rn是以天文單位表示的第n顆行星離太陽的平均距離，n是離太陽由近及遠的次序（但水星n=－∞為例外）。
1781年發現的天王星正符合n=8的位置上 ，因而促使人們去尋找n=5的天體，1801年果然發現了小行星，但這個公式物理意義仍不明確，因為在1846年發現的海王星、1930年發現的冥王星與該公式計算得距離偏離很大，故許多人至今持否定態度，認為充其量不過是幫助記憶的經驗式。隨著研究的深入，已提出了許多種行星距離公式，更常用的形式為an+1∶an=β（β為與行星質量有關的常數，而且在一些衛星系統中，規則衛星也同樣存在著類似關係，因此，該定則的物理意義還有待進一步探討。
行星及小行星帶軌道分佈
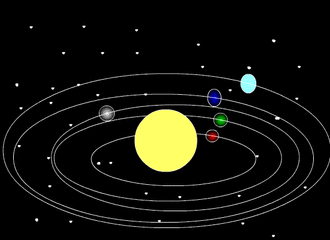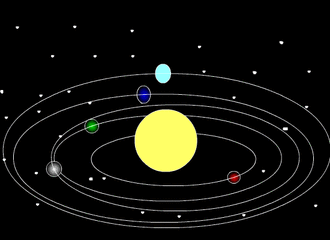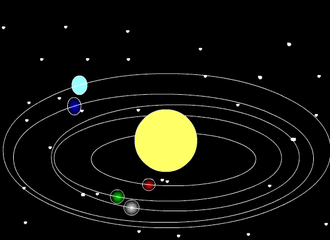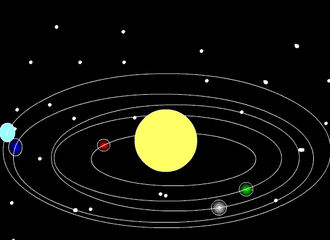
其實，仔細分析公式rn=0.4+0.3×2^n的拓展規律（n∈[0、1、2、3、4……]）就可以發現，這種分佈完全符合周長λ拓展呈對稱性原則，即其他行星軌道周長是以最內層行星軌道周長的2^n倍形式向外拓展的，用公式描述就是
將這種描述繪圖就如圖-2所示。
圖-2 . 2^n軌道拓展形式
原子中電子軌道分佈情況，我們是看不見摸不著的，對它軌道半徑或周長的n²倍拓展形式只存在於理論推理中，而太陽系行星軌道半徑或周長的2^n形式拓展形式是我們看得見摸得著的，而且也完全符合埃米·諾特對稱與守恆及拉格朗日最小作用量原理，結合玻爾軌道能級理論的侷限性，由此，我們可不可以做一個大膽推理：原子核外的電子分佈也應該符合2^n倍拓展形式，這樣微觀與宏觀世界的運動規律就是一樣的了，宇宙中也就不存在二套不能相容的支配規律，也就是說微觀與宏觀的運動規律也就具有了統一性。
太陽系行星運動
