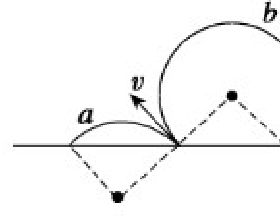
臨界狀態不唯一也是形成多解問題的其中一個因素。帶電粒子在洛倫茲力作用下飛越有界磁場時,由於粒子運動軌跡是圓弧狀,因此,它可能穿過去了,也可能轉過180°從入射面邊界反向飛出,如圖所示,於是形成了多解。當然,也有可能會構造其他的臨界狀態,這都需要我們會識別。
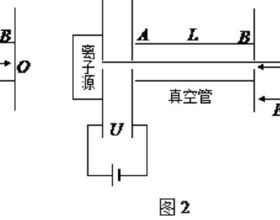
還是舉一道例題看一看。長為l的水平極板間有垂直紙面向裡的勻強磁場,如圖所示,
磁感應強度為B,板間距離也為l,板不帶電,現有質量為m、電荷量為q的帶正電粒子(不計重力),從左邊極板間中點處垂直磁感線以速度v水平射入磁場,欲使粒子不打在極板上,可採用的辦法是( )
A.使粒子的速度v<Bql/4m B.使粒子的速度v>5Bql/4m
C.使粒子的速度v>Bql/m D.使粒子的速度v滿足Bql/4m<v<5Bql/4m
解析: 構造直角三角形是帶電粒子在勻強磁場中運動軌跡問題解決的一個重要手段,大家要把握入射方向某點垂線和出射點如何構造直角三角形的方法。
帶電粒子剛好打在極板右邊緣,有r1²=(r1-l/2)²+l²,又因為r1=mv/Bq,解得v=5Bql/4m;粒子剛好打在極板左邊緣,有r2=l/4=mv/Bq,解得v=Bql/4m。所以D錯,B比C大,所以選AB,不過這種估算的準確率不是百分之百,算是死馬當活馬醫的時候的方法吧。
如果沒有時間也可以大致估算,顯然速度特別快或者特別慢的時候,粒子肯定無法打到板上。
如果你有今日頭條app,麻煩順手點一下關注@中學物理知識傳播者,每天都會傾情奉獻一段小乾貨,我會繼續努力的!