如有疑問且看本人的上一篇文章 在平坦宇宙中,平行線將永遠平行,物質,比如宇宙中的星系的平均分佈將呈現在我們面前,就如它的本來面目。這一假設狀態透過愛因斯坦的影象得到了證明:在平坦的幾何結構下,不發生任何扭曲。這一幾何狀態被直到現在為止對於深空的研究結果所證實。現在,天文學家相信:宇宙的膨脹並不再減速,而是在加速中。
在開放宇宙的情形下,空間有著雙曲面的形狀,像馬鞍樣。在這樣的幾何結構下,平行線最終背離。如果這種形狀下影象被投影到平坦表面上,我們能夠看到與球面上相反的扭曲:影象的中心被拉伸,外圍被壓縮。這意味著遙遠星系將看起來比鄰近星系更緻密。
閉合宇宙的幾何形狀如這裡的半球和變形的阿爾伯特·愛因斯坦的圖片所示(他本人並不相信宇宙是處於膨脹中的)。在球面上,平行線相交。如果愛因斯坦的標準影象被投影到球面上,再重新繪製到平面(就如我們在球面上看到的那樣)上,臉部的四周將被拉伸,而中心被壓縮。這支援了關於閉合字窗中遙遠星系將比鄰近星系看起來密度更低的見解。
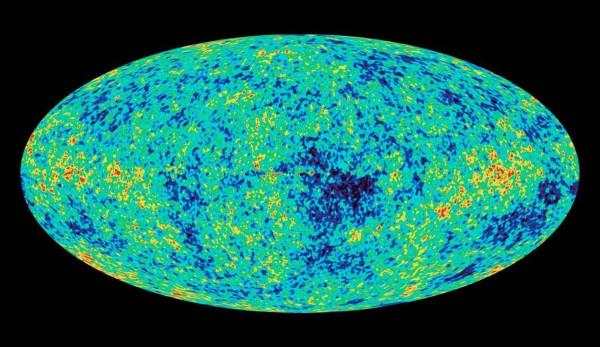
儘管天文學家有著計算恆星乃至星系中物質的量的可靠方法,但要計算整個宇宙中所有物質的重量並不那麼容易。天文學家轉而關注於我們看到的遙遠星系在宇宙上的曲率效應。如果空間在引力下是正曲率的,我們認為平行線將會最終相交,因此我們看到遙遠的星系的密度將下降。事實上對於深空的研究(如下圖)說明星系的分佈或多或少是調和的,這表明空間有著平均的幾何結構。對非常遙遠星系密度的研究同樣支援了這一結論:如果宇宙是閉合的,我們可以認為遙遠星系的密度下降。