迭代版本：161

本文，將會通俗易懂地介紹——量子態、波函式與粒子自旋的概念和影象，它們對於理解微觀世界的奧妙（難以理解）與玄妙（難以想象），有著十分重要且基礎的作用。

相信透過本文的描述，可以建立起對微觀粒子世界，更清晰深刻的理解和認知。

主題目錄如下：

• 什麼是量子態
• 什麼是波函式
• 量子態與波函式
• 什麼是粒子自旋
• 自旋影象
• 自旋是如何發現的
• 不同自旋的含義
• 複合粒子的自旋
• 結語
• 後記：自旋與化學的微妙關係

什麼是量子態

在量子力學中：

• 量子態——是由一組量子數所確定的微觀狀態。
• 量子數——是表徵微觀粒子運動狀態的一些特定數值。
• 量子——是不可分割的最小量（如光量子即光子，是光的最小量）。
• 量子化——就是存在非連續，呈現離散數值的最小量（量子）。

表徵——是指用資訊描述某一事物的狀態，即：資訊符號可以代替某一事物本身。

量子態中的每種量子數，都是量子化的非連續數值，其取值只能是“某個最小量”的整數或是半奇數倍，這個最小量就是量子，其數值與普朗克常數有關，即以普朗克常數為單位，而一個量子化的系統，至少需要一個量子數。

普朗克常數——可以理解為“作用量”的單位，即：能量 * 時間 = 動量 * 位移 = 普朗克常數的倍數。

作用量（Action）——是一個物理系統內在的演化趨勢；如一段運動的作用量，是動能與勢能之差對時間的積分；其數值為，能量 * 時間（S = Et）或動量 * 位移（S = px），單位和普朗克常數一樣（S = kh，k是倍數，h是普朗克常數）。

需要指出的是，光子碰巧是基本粒子，但並不是說量子就是基本粒子，只要是最小量即可——就如自旋角動量是最小量h / 2π的倍數，那麼最小量h / 2π就是量子，這個量子的倍數就是自旋量子數，即量子數以量子為單位——不過，如果把基本粒子看成“小份能量”的同義詞，那麼視其為量子的近義詞也未嘗不可。

h / 2π——稱為約化普朗克常數，h是普朗克常數，又寫作“ℏ”，讀作“h拔”。

量子數的數值，物理上代表著粒子可觀測到的狀態量，而在未觀測之前，這些數值出現的可能性是疊加和糾纏的，其中：

疊加——是指量子數的數值是不確定的，每個數值出現的可能性，都是一個機率，於是不同數值出現的機率，就可以疊加在一起，其總和是100%。

例如，自旋量子數，可以上自旋出現的機率是50%，下自旋出現的機率是50%這樣——上下自旋是Z軸上的方向，自旋在XY軸上也存在，即：X是左右自旋，Y是前後自旋——而上下自旋，就是量子數的兩種數值，對應了兩種量子態。

例如，薛貓的生死狀態，如果由一個量子數來決定，那麼量子數不同的數值，就代表了“生”的機率與“死”的機率，而在觀測之前，薛貓就是處在了量子數“生死數值”的疊加態。

糾纏——是指一個量子數在不同的子系統上，其不同的數值仍然會相互協調，表現為一個數值在子系統上確定，那麼與其疊加數值，在其它子系統上也會“瞬間”確定。

例如，一個自旋為0的粒子，衰變成了兩個糾纏粒子，每個粒子都是上下自旋的疊加態，如果一個粒子被確定是上自旋（即隨機到50%），那麼另一個糾纏粒子不用測量（即不用在50%中隨機）一定是下自旋——因為自旋會保持角動量守恆。

這就意味著，粒子的量子態是可以疊加和糾纏的，也就是通常所說的——量子疊加態與量子糾纏——前者就像是“上帝的骰子”，後者就像“上帝的意志”（即捉摸不定的運氣）。

實際中，量子數有很多種，其中自旋量子數，也就是粒子自旋，而在描述原子核外電子運動狀態時，有四種量子數：

• 主量子數（軌道能量層級，確定電子能級大小，正整數）。
• 角量子數（軌道空間角動量，確定電子雲形狀，正整數）。
• 磁量子數（軌道角動量的投影，確定電子雲方向，整數）。
• 自旋量子數（自旋的方向，確定電子自旋方向，半奇數）。

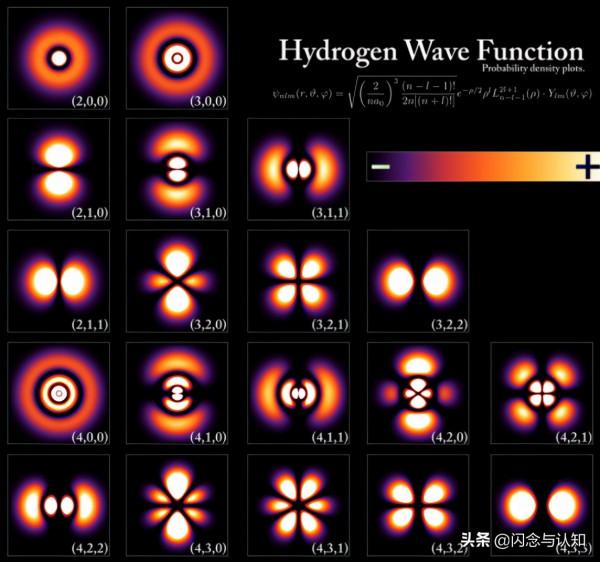
例如，下圖展示了氫原子的電子影象，包含了主量子數、角量子數、磁量子數——由於自旋量子數沒有空間可見性，所以沒有體現在影象中。

氫原子的電子雲，右下角數字代表的是（主量子數，角量子數，磁量子數）對應（1能級，2形狀，3方向），1代表不同的範圍大小，1相同2代表不同的形狀，2相同3代表不同的方向所看到的相同形狀，圖片來自維基百科（Wave function）

其它還有一些味量子數（Flavour），如重子數、輕子數、奇異數、同位旋等等，那麼多個量子數就可以共同描述一個量子態，其中每個量子數在觀測之前都是機率疊加，所以在觀測之前，量子態就是多個量子數所有機率的疊加。

也就是說，用多個量子數每個可能的數值，進行排列組合（即數量相乘得到組合數，可見量子數必須是離散的），而每個組合都對應一個量子態的機率（即由組合中每個量子數的機率相乘得到），所有這些量子態的機率是疊加的，其總和是100%。

最後，量子態涉及到一個——泡利不相容原理（Pauli Exclusion Principle），即：自旋半奇數的粒子（即費米子），其組成的系統，不能有兩個或兩個以上的粒子，處在相同的量子態；而自旋整數的粒子（即玻色子），其組成的系統，則可以有多個粒子，處在同一個量子態。

也就是說，費米子系統——不能有全同粒子，量子態可計數；玻色子系統——可以有全同粒子，量子態不可計數。

量子態相同，就沒有辦法計數的原因在於，粒子沒有明確的軌道，由於不確定性原理，它可以出現的位置是“機率雲”，所以就沒有辦法追蹤多個相同量子態中的一個，即不能給相同的量子態“編號”，這樣多個相同的量子態就沒辦法區分，只能算一個，同時測量還會改變全同粒子的量子態，使其變得不同。

什麼是波函式

在數學上，描述量子態的函式，就是——波函式，它是時間和空間的複變函式，其空間引數，是位置XYZ方向的三維組合，即ψ(x, y, z, t)，其結果是複數（也看成是復向量空間的向量），而它的表示式，是在具體的微觀條件下，由相應的薛定諤方程解出的。

複變函式（Complex Function）——是指以複數作為自變數和因變數的函式。

從某種角度說，薛定諤方程描述了粒子（包括原子及亞原子），其能量與動能、勢能的關係，即：總能量 = 動能 + 勢能——方程可以描述一對多的關係，函式只能描述一對一的關係——而薛定諤方程解出的波函式，則描述了粒子，其狀態與時間、空間的對映關係，這個對映關係在薛定諤方程中，就決定了粒子能量隨時間的演化，即：

總能量 * 波函式 = 動能 * 波函式 + 勢能 * 波函式。

需要指出的是，如果粒子的總能量是一個定值，即總能量不隨時間演化，這樣的粒子狀態就被稱為“定態”，那麼描述定態的薛定諤方程就不含時間，所以就被稱為“定態薛定諤方程”。

例如，原子內部的電子，就具有確定的能量狀態（即定態），它可以被定態薛定諤方程描述。

薛定諤方程——iℏ * (∂t)ψ(r, t) = (-ℏ^2 / 2m) * (∂r^2)ψ(r, t) + V(r, t) * ψ(r, t)，i是虛數，ℏ約化普朗克常數，r是XYZ座標，t是時間，∂t是波函式在t方向上的偏導，∂r^2是波函式在XYZ三個方向上的二階偏導再求和，m是粒子質量，V是粒子勢能。

方程等式的左邊是總能量，右邊是動能和勢能，即：總能量（波函式關於時間的變化，∂t）= 動能（波函式關於空間的變化，∂r^2）+ 勢能（波函式所在場的變化，V）——可見方程中，沒有一階以上的變數（線性）且有未知函式（波函式）及其二階偏導（微分），所以它是一個線性二階偏微分方程。

定態薛定諤方程——Eψ(r) = (-ℏ^2 / 2m) * (∂r^2)ψ(r) + V(r) * ψ(r)，E是粒子的總能量是一個定值，定態方程不含時間，也就是假設勢能V(r)和波函式ψ(r)都與時間無關，即不隨時間變化，這種不含時波函式稱為定態波函式，但其仍具有波動性，代表了粒子自身與時間無關的空間波動性。

事實上，量子力學中的薛定諤方程，就像是經典力學中的牛頓方程，它的表示式來自牛頓方程的“粒子化”，整個方程建立在各種假設之上，其正確性由實驗保證，並且它只適用於低速的非相對論粒子（狹義相對論），也不包含自旋描述——當涉及到相對論效應與自旋時，由狄拉克方程描述（其中也有波函式），可見狄拉克方程就像經典力學中的狹相方程。

有趣的是，“波函式”起初只是一個數學函式，雖然物理學家薛定諤，透過假設“湊出”了薛定諤方程，但他並沒有“理解”波函式，而是物理學家玻恩，對波函式做出了正確的“機率詮釋”，或說“統計詮釋”。

需要指出的是，物理學詮釋只是對“真理”的一種解釋，而解釋可以有很多種，所以物理學詮釋並不唯一，但得到共識且符合實驗觀測的詮釋，就可以獲得諾貝爾獎，如玻恩對波函式的機率詮釋。

相比解釋（Explain），詮釋（Annotation）不僅說明原因關聯，還具有某種代表性的獨特理解。

那麼，之所以稱之為波函式，是因為薛定諤方程在數學上，是一種型別的波動方程，而波函式又產生並解釋了粒子的波粒二象性，所以描述量子態的函式，其實是在描述一種“波”。

在物理上，波函式的影象，即ψ(x)，就代表了粒子位置的機率分佈（類似正弦波的形狀），其模平方，即|ψ(x)|^2，就是粒子位置的機率密度，而透過機率密度可以得出，粒子在某位置的機率。

需要指出的是，波函式的物理意義——是量子力學（哥本哈根學派）的一個基本假設，不需要推導，也不需要解釋，只需要預設接受即可。

換言之，波函式是粒子的機率分佈函式，取值為複數，物理意義為機率幅度（Probability Amplitude）；波函式的模平方是粒子的機率密度函式，取值為正實數，物理意義為區域機率。

縱軸是波函式的實部，藍線是機率幅度，紅線是區域機率，紅色透明度代表了粒子在x位置出現的機率，圖片來自維基百科（Wave function）

機率分佈函式——取值是小於某值的機率，如：P = F(b)，這個機率是小於某值（b）的機率累加，那麼它可以計算某個區間的機率，如：P = F(b) - F(a)，而區間斜率越大，說明機率的變化率越大，即F(b) - F(a)越大，也就是機率越大，這個變化率（或說導數）就是機率密度。

機率密度函式——取值是機率的變化率，那麼它在某個區間的面積越大，就是隨機到其中的機率越大，也就是機率密度的面積（或說積分）是某個區間的機率分佈，而這個變化率越大，如f(a)越大，表明在該點（a）附近的機率越大，但不是該點（a）的機率越大，不過這個變化率可以理解為，在該點（a）無窮小區域內的機率。

複數的模——就是係數平方和的平方根，如：|a + bi| = |a - bi| = sqrt(a^2 + b^2)。

從物理角度繪景，波函式就像是一個“複數場”，場裡的每一個複數都是波的幅度，其模平方是波的機率，其方向（即復向量的向量角）是波的相位。

相位（Phase）——就是一個波，其迴圈中的位置，如：波峰、波谷、或是峰谷之間某個點的標度。

需要注意的是，波函式的干涉疊加，是機率幅度的疊加，而不是機率（即模平方）的疊加，兩者是有區別的，即：“先相加再模平方”與“先模平方再相加”的區別；如：|0.1 + 0.1|^2 = 0.04與|0.1|^2 + |0.1|^2 = 0.02的結果是不一樣的。

綜上可見，波函式就是粒子所具有的機率波動性，因此波函式也被稱為——機率波，或波粒二象性中的物質波。

量子態與波函式

具體來說，量子態與波函式有著微妙的關係，即：

量子態在數學上稱之為“態向量”（State Vector，或稱“狀態向量”），它是復向量空間上的一個復向量——關鍵在於，態向量（即量子態）在被波函式描述之前，是“不可見”的，這就像一個向量必須被投影到座標系上，才能描述出來被“看見”——可見波函式，其實是量子態（即態向量）在座標系上的投影。

需要指出的是，物理上的向量就是數學上的向量，向量存在於真實空間，向量存在於數學空間，所以態向量在物理上被稱為“態向量”，而由於態向量（數學抽象）必須由波函式（座標表象）描述，所以波函式也被稱為“態函式”，態向量則可以簡稱為“態”。

換言之，量子態這個向量，在某些基底（即基向量）方向上的投影，就是波函式，所以波函式也是一個向量（可以用一維矩陣表示這個波函式向量），只不過這個向量具有機率波動性——其模平方就是，粒子在此向量處出現的機率，而這個向量可以看成是，波函式“波形影象”的相位。

那麼顯然，一個向量可以由多個基底方向上的向量來線性疊加組合，所以一個量子態就可以由多個波函式線性疊加組合來描述，而每個波函式都是一個量子態的投影，這意味著一個量子態可以由多個量子態線性疊加表示，即：量子疊加態（它是薛定諤方程的一個解）。

需要注意的是，波函式ψ(x)所有的取值，都是其向量的分量，每一個分量也是向量——分量代表了波函式“波形影象”上某處的幅度和相位——如果有無窮多個分量（如位置座標），疊加態就要使用積分代替求和。

可見，波函式蘊含了所有可能的狀態，每一個狀態都是一個向量，而所有這些向量之和，則就是“波函式向量”。

例如，量子態ψ，由量子態ψ1和ψ2疊加，即：|ψ> = a|ψ1> + b|ψ2>，符號“| >”中的ψ、ψ1、ψ2只是一個名稱用於標識量子態、量子數或物理操作等，而每一個“| >”都是一個基底量子態，前面的係數a、b的值是複數，也就是波函式對應的取值，所以係數就是波函式，代表了這個量子態出現的機率。

量子態的符號——量子態ψ，用右矢“|ψ>”或左矢“<ψ|”表示，由於其數值是一個複數，所以右矢和左矢就是共軛複數，即實部相同且虛部不同的複數，而從向量角度看，右矢|ψ>是一維列向量，左矢<ψ|是一維行向量。

需要指出的是，基底量子態又稱為“本徵態”（Eigen State），通俗地說，就是可以被觀測到的量子態，從這個角度看，量子疊加態就是——任意多個可以被觀測到的本徵態的係數線性疊加（也就是波函式的線性疊加），並且所有係數對應的機率相加必須得到100%，即：實際中必須要能（也只能）觀測到，任意多個本徵態中的某一個。

需要注意的是，波函式雖然是複數，但其投影的本徵態的複數軸可能為0（即與複數軸垂直），此時這個本徵態對應的係數（即波函式、複數、向量）就沒有虛數i。

例如，|薛貓生死態> = a|生的本徵態> + b|死的本徵態>，其中a（波函式、複數、向量）決定了生的機率，b（波函式、複數、向量）則決定了死的機率——如果生或死的機率都是50%，那麼a = 1 / sqrt(2)，b = i / sqrt(2)，|a|^2 + |b|^2 = 1，這裡假設要求本徵態的機率之和是100%——如果是兩個波函式的干涉疊加，則其機率是|a + b|^2，而不是|a|^2 + |b|^2。

本徵（Eigen）——就是事物本身的特徵。

在數學上，可用公式表達，即：pf = cf，p是操作，f是對映，c是常數，意思是一個對映的操作結果等於這個對映的常數倍，可見這個操作的效果就是常數倍的縮放，所以常數（c）就是操作（p）的本徵值（Eigen Value）。

在物理上，操作p就是一種物理變換（也稱算符），對映f（數學上稱運算元）可以是函式（態函式）或向量（態向量），所以可以稱之為本徵態（Eigen State）或本徵向量（Eigen Vector），可見本徵態和本徵向量經過算符的操作，只是縮放其狀態和方向不變。

事實上，波函式也可以用量子態的符號表示，那麼上述量子態疊加就可以寫成：|ψ> = |a> <a | ψ> + |b> <b | ψ>，其中<a | ψ>就是量子態ψ在本徵態a方向上的投影，<a | ψ>就是波函式ψ(a)，其模平方就是量子態ψ在本徵態a方向上出現的機率。

所以，波函式有兩種表示形式：

• 從ψ(x)函式形式看——是將x對映到一個複數；
• 從<x | ψ>量子態形式看——是將量子態ψ投影到本徵態x。

而向量的投影，其實就是向量的內積，因此<x | ψ>就是量子態ψ與本徵態x的內積——可見波函式ψ(x)，就是向量內積的產物。

那麼，如果x不是本徵態，而是另一個量子態ψ2 ，此時<ψ2 | ψ1>就表示波函式ψ1和波函式ψ2的內積，意思是量子態ψ1坍縮到量子態ψ2的機率（這是玻恩規則，量子力學的一個基本假設），其結果仍然是一個波函式、複數、向量——自然也是量子態ψ1到量子態ψ2的投影。

但一個波函式與其自身（共軛複數）的內積，就表示其模平方，即：<ψ | ψ> = |ψ|^2，意思是（前面所說的）量子態ψ的機率密度，其結果是一個正實數——可以理解為，自身的投影就從“複數世界”投影到“實數世界”去了。

而如果一個波函式，是疊加態（或稱混態）則<ψ | ψ> = 1（這是量子力學的一個基本假設，即這個向量的空間內積被歸一化），是非疊加態（或稱純態）則<ψ | ψ>小於1，表示疊加態（如薛貓生死態）在某個本徵態（如薛貓生的態）上的投影機率。

回到量子數的角度，一個粒子的量子態，可以由多個量子數描述，所以波函式其實是描述了多個量子數疊加的機率分佈，如：ψ(r, p, E, s, t)，r是位置，p是動量，E是能量，s是自旋——這相當於，將連續（如位置）和離散（自旋）的變數都放到了一個多維向量中來描述。

換言之，波函式可以給出特定“位置、動量、能量、自旋”狀態粒子的機率分佈——其機率依然是波函式的模平方，即：|ψ(r, p, E, s, t)|^2——事實上，所有的量子數都與“位置、動量、能量、自旋”有對應關係，因此波函式就可以描述所有的量子數。

需要指出的是，在數學上，函式的一個引數就是一個維度，而超過四維引數（即三維位置和一維時間）的超空間，都可以投影到四維的位置空間或動量空間。

因為，時間與能量有對應關係（時間平移對稱性的守恆量是能量），空間與動量有對應關係（空間平移對稱性的守恆量是動量）——別忘了，物理系統的演化，可以用“作用量”描述，而作用量 = 能量 * 時間 = 動量 * 位移 = 普朗克常數的倍數——所以波函式可以寫成，隨時間與能量變化的位置函式（對應位置空間）與動量函式（對應動量空間）。

那麼，觀測一個粒子的量子態，就相當於獲取了粒子的量子數，於是波函式對應的機率密度，就會坍縮到一個確定的點上，即機率隨機出結果（觀測到本徵態），這也就是——“波函式坍縮”，而此時，波函式就演化成了一個“確定態”的函式（不再具有“疊加態”），於是粒子的波動性也就變成了粒子性。

最後，總結一下，量子態是一個數學抽象，需要用波函式具體描述（表示），那麼：

• 在數學上，波函式映射了，複數（函式值）與時間、空間（函式引數），其影象是一個波形，而將複數看成復向量空間的一個復向量，則波函式代表了所有映射向量的疊加向量，即態向量（也是一個復向量）。
• 在物理上，波函式映射了，粒子狀態的機率幅度（函式值）與時間、空間（函式引數），其影象是一個機率分佈，而將機率幅度的模平方看成是機率，則波函式包含了所有狀態機率的疊加機率，即量子態（也是一個態向量）。

可見，數學描述了量子態（疊加向量），物理則詮釋了量子態（疊加機率）。

什麼是粒子自旋

粒子自旋——是粒子的重要屬性，可以用來對粒子的標識和分類，因為每個粒子都有特有的自旋，自旋數不同就是不同類別的粒子，性質也不同。

但粒子自旋，並不對應宏觀上的物體自轉，如：陀螺自轉、地球自轉——因為點粒子沒有轉軸以外的部分（其它點），也沒有更小單元圍繞質心自轉。

所以，粒子自旋是唯象（Phenomenology）的描述，僅能將自旋視為一種內在性質，是粒子與生俱來帶有的一種角動量。

角動量——是質點矢徑掃過面積的速度大小，或是剛體定軸轉動的劇烈程度 。

而自旋具有可觀測的量子化數值——無法被改變，但其方向可以透過一些操作來改變，並且自旋（角動量）與方向（角度）遵循不確定性原理，即：自旋可以分解到XYZ座標軸方向，每個方向的自旋就會此消彼長——也就是說，確定一個Z方向的上下自旋，就不能確定另外XY方向的自旋。

弦理論專家——布賴恩·格林（Brian Greene），在《宇宙的琴絃》中，指出：

“宇宙的每一個電子，總是永遠地以固定不變的速率旋轉。電子自旋不是我們習慣的那類物體偶然發生的短暫的旋轉運動，而是一種內稟的性質，跟它的質量和電荷一樣。如果電子沒有自旋，它也就不是電子了。”

自旋影象

一個自旋糾纏的光子，“翅膀”就是疊加態的自旋，圖片來自影片《宇宙時空之旅：未知世界》

最後“翅膀”合併了，是量子自旋糾纏態坍縮了，圖片來自《宇宙時空之旅：未知世界》

自旋是如何發現的

首先，是在斯特恩-蓋拉赫實驗中（Stern-Gerlach Experiment），發現了銀原子束經過不均勻磁場，產生了偏轉，並最終在螢幕垂直方向上，形成了兩個上下對稱的非連續分佈。

預期是一條線，實際是兩個點，圖片來自維基百科（Stern-Gerlach Experiment）

這裡有兩個奇怪的事情：

第一，為什麼銀原子電中性，會被磁場影響？

這是因為，銀原子有一個非配對電子，這個電子繞著原子核的軌道運動，形成了閉環電流，而閉環電流會產生磁矩，正是這個磁矩，讓銀原子產生了偏轉。

磁矩——就是磁場中的磁性力矩，方向垂直於線圈所在平面，且當電流方向為逆時針時磁矩為正，順時針時為負。

需要注意的是，如果是均勻磁場，閉環電流的磁矩就是0，只有不均勻的磁場，才能產生垂直方向上的磁矩。

第二，為什麼螢幕上，預期是連續分佈，但實驗結果卻是非連續分佈？

這是因為理論上，銀原子電子的磁矩方向，是隨機連續的，其取決於電子的軌道角動量——也就是說，電子雲與垂直方向有一個隨機連續的角度。

那麼，擁有不同磁矩方向的銀原子，進入不均勻磁場，就會有不同的固定偏轉，而大量不同磁矩方向的銀原子，最終在螢幕垂直方向上，就應該是隨機連續分佈的。

而實驗結果表明，電子的軌道角動量不是連續的，而是量子化的，也就是電子雲與垂直方向的角度只有兩個固定值，所以銀原子的磁矩就只有上下兩個固定值。

但如果是這樣，就會存在一個問題，就是根據理論：

• 軌道角量子數，只能是正整數，即：l = 0，1，2，等等中的一個。
• 軌道磁量子數，受制角量子數，即：針對每一個角量子數l，磁量子數都可以取值為——從+l到-l之間的整數，如：l = 1對應1，0，-1；l = 2對應2，1，0，-1，-2——也就是有2l + 1個可能的數值，代表著磁矩可能的方向。

那麼在實驗中，銀原子的磁矩有上下兩個，即：2l + 1 = 2得出l = 1 / 2，然而電子角量子數——並不能等於非正整數。

要解決這個問題，就可以假設電子自身，擁有一個半奇數（1 / 2）的自旋量子數，然後自旋角動量磁矩與軌道角動量磁矩，其“合磁矩”才是銀原子（基態）的兩個磁矩。

這等同於說，銀原子角動量 = 電子軌道角動量 + 電子自旋角動量——於是，電子自旋就被引出了。

其次，在實驗之後，物理學家狄拉克，用狄拉克方程解出了“自旋解”——它是狄拉克方程內在的數學要求。

至此，所有的粒子從理論上就都有了——自旋。

不同自旋的含義

粒子的自旋角動量，是可觀測的量子化數值，其值是——自旋量子 * 自旋量子數 ，其中自旋量子是h / 2π，而自旋量子數是整數或半奇數，可正負代表了不同的自旋方向。

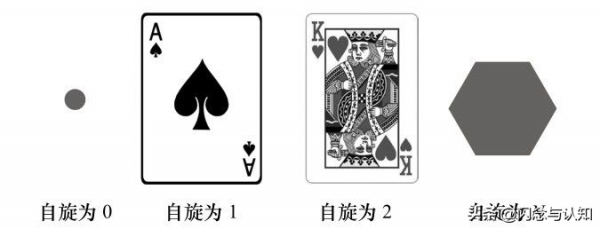
• 自旋為0——粒子，從各個方向看都一樣，就像一個點（如希格斯玻色子）。
• 自旋為1——粒子，在旋轉360度（1圈）後看起來一樣（如光子、膠子）。
• 自旋為2——粒子，在旋轉180度（1 / 2圈）後看起來一樣（如引力子，未證實）。
• 自旋為1 / 2——粒子，在旋轉720度（2圈）後才會看起來一樣（如電子、中微子、夸克）。
• 目前發現的粒子中——自旋為整數的，最大自旋為4，自旋為半奇數的，最大自旋為3 / 2。

A中黑桃的方向360度還原，K中人物的方向180度還原，圖片來自《物理史話》

事實上，自旋為s的粒子通常有2s + 1種自旋，如：自旋1 / 2的電子有2種自旋，自旋1的光子有3種自旋，自旋為0的希子（希格子玻色子）有1種自旋。

那麼，對於自旋1 / 2，反映到波函式（即機率波的影象）上——就是粒子轉一圈之後，波函式的相位會與原來的正好相反，只有轉2圈，波函式才能徹底恢復原狀。

當然，直接測量波函式的相位，是不可能的，但是我們可以測量相位差。 就像雙峰干涉實驗一樣，相位差不同的兩束波，疊加在一起會發生干涉現象。這樣的話，透過干涉條紋的分佈，就可以計算出相位差，也就可以證明粒子自旋，確實是1 / 2了。

不過，在現實中，物理學家費曼曾用水杯演示了，需要旋轉2圈（即720度）才能復原的情況，如下圖所示：

費曼的水杯自旋表演，360度到540度，需要手過頭頂才能完成，圖片來自科學網《統一路-7-奇妙的旋轉2》

那麼，對應到泡利不相容原理，在費米子系統中，粒子的量子態之所以不能相同，就在於費米子自旋整數圈不能對稱，只有自旋半整數圈才對稱。

這意味著，費米子波函式不具有交換對稱性，只有交換反對稱性，即：交換費米子位置，其波函式就會改變正負號。

因此，費米子波函式的對稱中心點，就必須是0（否則就沒有反對稱性），而這個點，就是量子態相同的點，其出現費米子的機率是0，即：沒有量子態相同的費米子。

對此，英國粒子物理學家——布萊恩·考克斯（Brian Cox），在《量子宇宙》中，指出：

“可以證明，自旋就是不相容原理的原因，因此也是原子結構之所以如此的原因……現在我們知道了，我們鞋的原子包含的電子與地面的電子，不僅是由於同性電荷相斥而相互推開；根據泡利不相容原理，它們也因自然的互相避開而排斥。”

可見，正是自旋帶來的相互排斥力（即簡併壓力，Degeneracy Pressure），才使得原子具有結構穩定性，從而支撐了原子之上的結構穩定性——顯然，這也是我們體內原子具有結構穩定性的原因所在。

複合粒子的自旋

複合粒子，是由基本粒子構成的，基本粒子是不可再分的點粒子。這裡不可分割的意思，是指沒有體積與模型影象，無法檢測到其內部結構，如：光子、電子和夸克。

那麼，複合粒子的自旋——就是其內部各組成部分之間，相對軌道角動量和各組成部分自旋的向量和，即：按照量子力學中，角動量相加法則求和，如質子的自旋——可以從夸克和膠子的自旋得到。

結語

綜上可見，量子態透過多個量子數，描述了微觀粒子的運動狀態，量子數代表的，就是微觀粒子，最小的不可分割的一個狀態性質，可以稱之為——“自由度”。

而自由度，可以理解為狀態呈現的一些數值——這些數值是量子化的，即不連續、跳動、隨機的，顯然這是非常“自由”的，所以波函式也是自由度的函式。

在眾多量子數中，自旋是所有微觀粒子，所普遍共有的，那為什麼所有的粒子都要自旋呢？

這和波函式坍縮一樣，目前是一個未解之謎。

後記：自旋與化學的微妙關係

我們知道，化學元素即是原子，而元素的化學性質，是由原子其核外電子的數量與排列，所決定的——於是，元素的化學性質，就和電子繞核運動所具有的能量，關聯在了一起。

由前文可知，電子繞核運動的狀態，由四個量子數來描述，即：主量子數（n），角量子數（l），磁量子數（m），自旋（s）——而它們之間約束關係，就決定了核外電子的數量與排列，即元素的化學性質。

具體來說：

• n是電子的能級，取正整數，如：n = 0，1，2，3，等等。
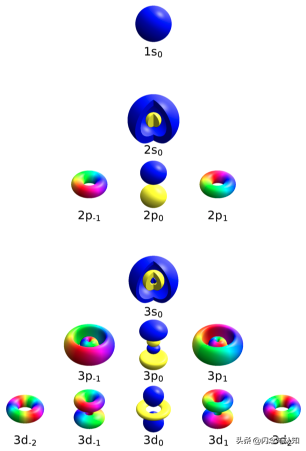
• l是電子的形狀，取正整數，且每個n對應[0, n-1]個l，如：n = 1對應l = 0；n = 2對應l = 0，1；n = 3對應l = 0，1，2；即：l = n。
• m是電子的方向，取整數，且每個l對應[-l, +l]個m，如：l = 0對應m = 0；l = 1對應m = -1，0，1；l = 2對應m = -2，-1，0，1，2；即：m = 2l + 1
• s是電子的自旋，取半奇數，固定對應兩個數值，即：- 1 / 2與+ 1 / 2。

那麼，代入物理意義就是，電子在特定的能級（n）只能有數量有限的形狀（l = n），在特定的形狀（l）只能有數量有限的方向（m = 2l + 1），在特定的方向（m）只能有兩個自旋數值——所以，m個方向就有2m個不同的電子。

於是，電子數量就被能級給固定了，即：電子數量 = 2m = 2(2l + 1)，且l = [0, n-1]，如：

• 能級n = 1則l = 0——可以容納2個電子。
• 能級n = 2則l = 0，1——可以容納2 + 6 = 8個電子。
• 能級n = 3則l = 0，1，2——可以容納2 + 6 + 10 = 18個電子。

類氫原子軌道，從上到下：能級大小n = 1，2，3；軌道形狀l = 1（s軌道），2（s-p軌道），3（s-p-d軌道）；軌道投影方向m = 1s，1s + 3p = 4，1s + 3p + 5d = 9；自旋沒有空間可見性，圖片來自維基百科（Quantum number）

至於，為什麼一個能級在一個形狀和方向上，最多隻能放2個電子——這是前文所提到的，泡利不相容原理的要求，即：電子的量子態不能相同，而電子自旋只有兩個數值，來區分相同形狀和方向上的量子態。

更為底層的一個原理是，萬物總是趨向於處在最低能量狀態——對原子來說，就是總是傾向於用電子填充其能級（否則就會增加其自身的能量），於是原子就會有動力與相鄰的原子共用電子，而這就是化學作用的基礎。

例如，氫原子外層n = 1能級有1個電子，但可以填充2個電子，於是它與另一個氫原子共用1個電子，就形成了氫分子H2。

例如，碳原子有兩個能級，外層n = 2能級有4個電子（內層n = 1有2個電子，一共6個電子），但可以填充8個電子，於是再結合4個氫原子的電子，就形成了甲烷CH4。

例如，氧原子有兩個能級，外層n = 2能級有6個電子（內層n = 1有2個電子，一共8個電子），於是再結合2個氫原子的電子，就形成了水H2O，而它也可以一對結合一個碳原子的4個電子，從而形成二氧化碳CO2。

可見，正是自旋決定了原子核外電子的排列方式，才形成了元素之間相互結合的驅動力，最終才形成了從氫、氧、碳、到水與基因，等大自然中的萬物。