基於量子霍爾效應發展而來的拓撲絕緣體是凝聚態物理重要的科學前沿之一。其最為鮮明的特點是存在拓撲非平庸的能帶結構，通常由拓撲不變數描述。量子反常霍爾效應（又稱陳絕緣體），無需外磁場和朗道能級，因而有更高的實際應用價值。對應的拓撲不變數為第一陳數，由貝利曲率在布里淵區上的積分給出，描述系統的整體拓撲性質。當波函式不存在奇點時，積分將嚴格為零，導致拓撲平庸的絕緣態。

為了對陳數有更加深入的瞭解，北工大理論物理系博士生常治文，在導師劉鑫教授和北航物理學院郝維昌教授指導下，基於兩帶模型提出了一種新的拓撲規範理論[1]，關注於拓撲缺陷的微分結構。以哈密頓量和布洛赫波函式為基本場，構造 ’tHooft單極模型，波函式的奇點誘匯出單極（monopole）和半子（meron）兩種拓撲激發。經計算發現，在單極缺陷處，系統能隙閉合，處於金屬態；此時將有拓撲相變發生。在半子缺陷處，系統具有有限大小的能隙，處於絕緣態；但同時能帶具有非平庸拓撲，半子的拓撲荷將給出系統的陳數。該理論能夠給出與文獻中相同的結果，同時為實現高陳數模型提供了新的思路。

將上述理論應用於下面的模型中，得到了與文獻中相同的結果

hx = sinkx , hy= sinky , hz= m + coskx + cosky

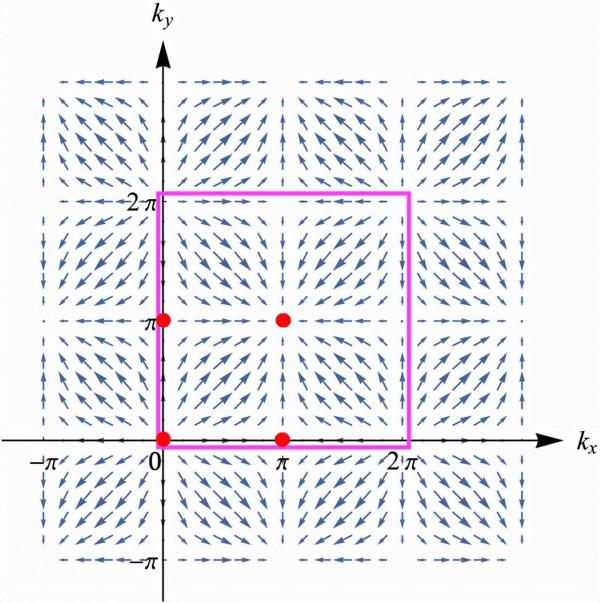
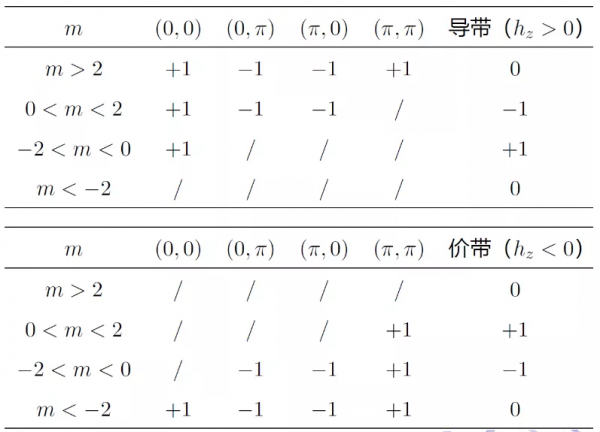
單極拓撲激發是一種三維拓撲缺陷，其位置座標滿足hx =hy = hz = 0。在這些奇點處，系統能隙為零，發生拓撲相變。半子是一種二維拓撲激發，其位置座標滿足hx =hy = 0， hz≠ 0。透過觀察向量場(hx , hy)在半子周圍分佈，可得到其拓撲荷（圖1）。進一步，根據hz在半子處的取值，將得到不同能帶的陳數（表1）。

圖 1：半子拓撲缺陷是一種二位拓撲激發：(0,0)/(π,π)處為源點/匯點，拓撲荷為+1；(0, π)/(π,0)處均為鞍點，拓撲荷為-1。方框區域為第一布里淵區。

表格 1：導帶和價帶的陳數

實現高陳數的量子反常霍爾效應是當前研究的重點方向之一。無耗散的邊緣態（即縱向電阻為零）可用於設計積體電路中的連通器，其效能主要依賴於邊緣態與正常金屬電極之間的接觸電阻。陳數越大，接觸電阻越小，器件效能越高。2020年，實驗上在多層結構中實現了高陳數[2,3]：將多層相同的量子反常霍爾薄膜堆疊在一起, 中間由普通絕緣體層隔開,可形成具有等效高陳數的體系。如果未來能夠在單層結構中實現高陳數，將會是一個重要的突破。我們提出如下高陳數模型，並利用拓撲激發計算陳數，得到的結果與傳統計算方法相同。

hx = sin2kx , hy= sin2ky + sinky, hz = m + cos2kx+ cos2ky + cosky

單極拓撲激發位於能隙閉合處，系統發生拓撲相變；半子的拓撲荷由向量場(hx, hy)的分佈確定（圖2）。

圖 2：高陳數模型中的半子拓撲激發：(0,0), (0,π),(π,0), (π,π)處均為源點，拓撲荷為+1; (π/2,2π/3), (π/2, 4π/3), (3π/2, 2π/3), (3π/2, 4π/3)處均為匯點，拓撲荷為+1;(0, 2π/2), (0, 4π/3), (π/2, 0), (π/2, π) (π, 2π/3), (π, 4π/3), (3π/2, 0), (3π/2,π)處均為鞍點，拓撲荷為-1。

根據hz在半子處的取值，給出不同能帶的陳數：

物理上，該模型可能在單層長方晶格中同時考慮次緊鄰躍遷和自旋軌道耦合實現。

[1] Zhi-Wen Chang, Wei-Chang Hao, and Xin Liu. A gauge theory fortwo-band model of Chern insulators and induced topological defects. Commun.Theor. Phys. 74: 015701, 2022.

[2] Y. Deng, Y. Yu,M.-Z. Shi, et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science, 367:895-900, 2020.

[3] Y.-F. Zhao, R.Zhang, R. Mei, et al. Tuning the Chern number in quantum anomalous Hall insulators. Nature, 588:419-423, 2020.