複合材料力學 致力於複合材料力學與模擬分析領域知識創作與分享! 586篇原創內容 -->
導讀
聚合物複合材料的製造過程中,需要將模具和鋪放的預浸料置於受溫度迴圈控制的熱壓罐內。熱壓罐內的高溫可以固化聚合樹脂,進而形成最終的複合材料產品。這一熱化學過程原理是確定的,並可由一組耦合的非線性偏微分方程表示,來描述熱傳導和樹脂固化動力學。然而,這些偏微分方程的解不是封閉的,需要近似計算。為此,加拿大不列顛哥倫比亞大學Sina Amini Niaki(第一作者&通訊作者)及其團隊在《Computer Methods in Applied Mechanics and Engineering》上發表了題為“Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture”的文章,對物理資訊神經網路(PINN)方法進行了新的改進,旨在解決在高壓釜中複合固化的模擬,透過在不同材料厚度及熱邊界條件下的多個場景下,PINN法得到了驗證。
內容簡介
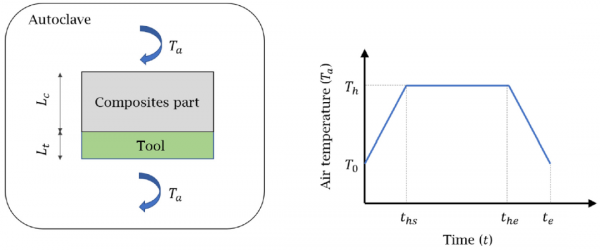
物理資訊神經網路(PINN)方法可以訓練深度神經網路(DNN)模型,使一組訓練點(稱為取樣點或配置點)直接滿足偏微分方程式(PDE)。透過引入基於偏微分方程的損耗函式、初始條件,和邊界條件殘差,不再需要使用任何其他模型或模擬,PINN就可以恢復PDE的解。PINN與有限元方法以及其他替代模型相比具有許多優點:不需要基於網格的空間離散或複雜的網格生成;在已知精度的條件下滿足所有訓練點的微分方程的形式;支援在同一個框架中整合資料和數學模型,並可以構建代理。因此,PINN方法的許多變式已經成功地廣泛應用於工程中。在該研究中,作者重點求解圖1所示的複合系統的微分方程組。在這個雙材料系統中的傳熱是由微分方程組控制的。然而,在複合材料與模具材料的介面交點處,材料效能是不連續。
|
(a) |
(b) |
圖1 (a)高壓釜內複合材料-模具材料系統示意圖(b)高壓釜在製備過程的空氣溫度歷程圖。
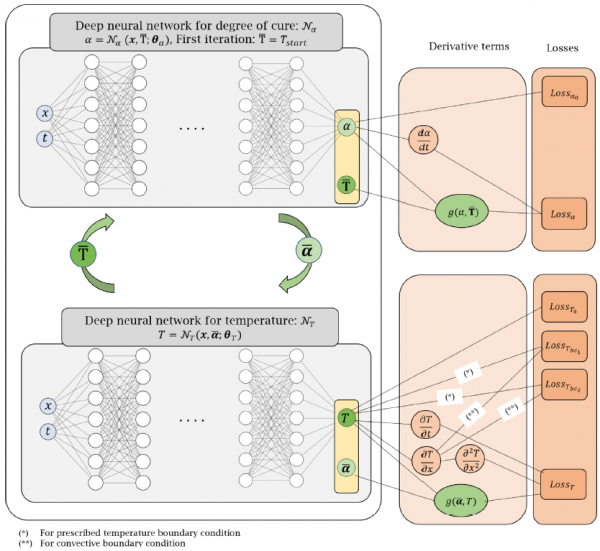
標準物理資訊神經網路原理圖如圖2所示。
圖2 一個具有空間、時間輸入特徵(x,t)、固化度和溫度輸出(α,t)的單一神經網路結構的示意圖,且透過控制方程、初始和邊界條件的損失項組成的總損失函式對網路結構進行多目標最佳化
圖3表明標準的最小化演算法不能將輸出相關的損耗降低到可接受的水平。作者使用了經典的求解方法(例如有限元法),另外,每個輸出都是獨立逼近的,沒有共享的自由度。圖4為網路的結構示意圖與順序訓練過程。
|
(a) |
(b) |
(c) |
圖3 網路訓練中不同損耗項的演化(a)聯合網路架構,5層42個節點(共7436個引數)(b)同時訓練的不相交網路結構,每個網路有5層30個節點(共7682個引數)(c)一種不相交的網路體系結構,採用提出的順序訓練過程,每個網路有5層30個節點(共7682個引數)
圖4 單一材料系統的網路結構示意圖。T和α分別構造兩個獨立的網路,先在α上進行序列訓練,然後在T上進行序列訓練,直到收斂
對於雙材料複合材料-模具體系,固化度僅適用於複合材料。然而,溫度分佈被定義為模具和複合材料部件兩部分。解空間的有關定義如圖5所示。
圖5 一個用於雙材料問題的不連續網路結構的示意圖。將兩個獨立的網路T-和T+與Heaviside階躍函式H結合,進而構造T的解空間
PINN提供了一種不依賴於大量預生成資料的代理的自然構造。特別是,可以簡單地擴充套件DNN,將問題引數作為輸入,並在這些問題引數的期望範圍內複製一組值的原始訓練損失函式集合。這種方法不需要來自單獨的高保真模擬的任何額外資料,但可以自然地包括任何具有額外損失的可用資料。例如,圖6顯示了PINN固化的溫度和固化度,並添加了一個附加引數ζ,從而建立了一個替代複合材料-模具系統模型。一旦經過訓練,該模型幾乎可以實時預測反應變數。
圖6 用於構造一個基於pin的代理模型的網路結構示意圖,模型中包含一個額外的輸入變數ζ。訓練後,該模型可預測在在時空域上任何新的輸入變數的溫度和固化度
為了檢驗PINN方法在預測溫度和場變數時的準確性,將結果與有限元預測結果進行了比較。有限元離散化包括案例1與2的35個單元和案例3與4的260個單元。所有情境下均有926個時間步長。圖7和圖8顯示了對案例1和2溫度和固化度的預測。
|
(a) |
(b) |
圖7 PINN和FEM溫度預測(a)案例1(b)案例2。(頂行)使用PINN預測溫度(第二頂行)使用FEM預測溫度(第三頂行)PINN和FEM預測溫度的絕對誤差。(底部一行)溫度微分方程的殘差
|
(a) |
(b) |
圖8 PINN和FEM固化度預測(a)案例1和(b)案例2。(頂行)用PINN預測固化度(第二頂行)用FEM預測固化度(第三頂行)PINN和FEM預測固化度的絕對誤差。(底部一行)固化度微分方程的殘差
小結
作者提出了一種PINN框架,用於模擬複合材料-模具系統經歷完整的固化迴圈的放熱傳熱情況,解決了複合材料-模具材料中兩個耦合微分方程的解,即在放熱傳熱和樹脂反應時溫度和固化度分佈和演化的規律。
原始文獻:Niaki SA, Haghighat E, Campbell T, Poursartip A, Vaziri R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 384:113959.
稿件整理:Sophia (感謝投稿)