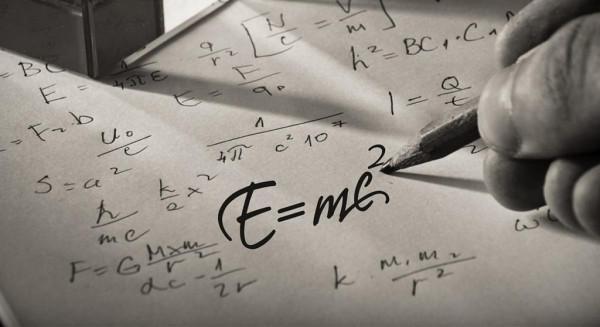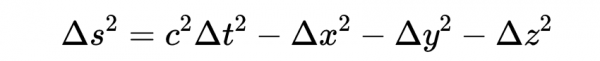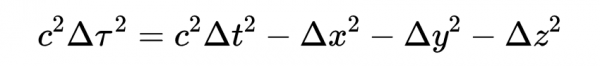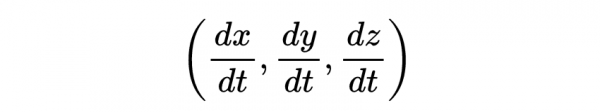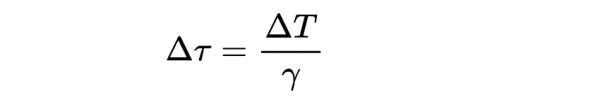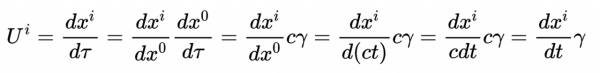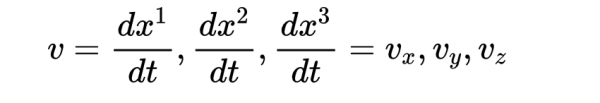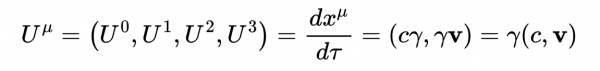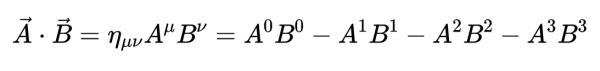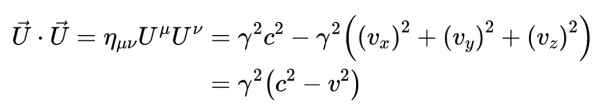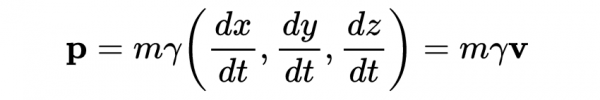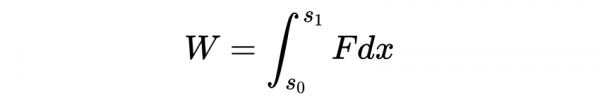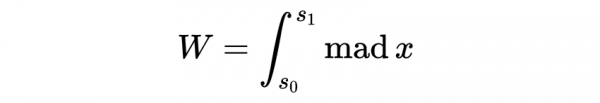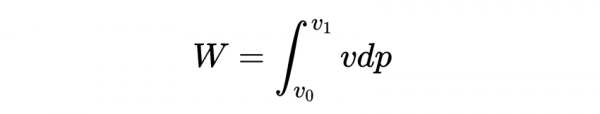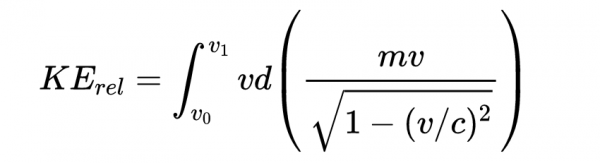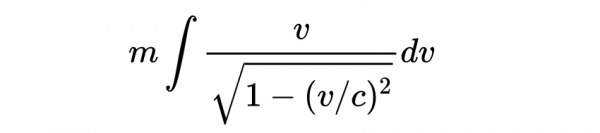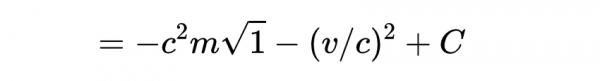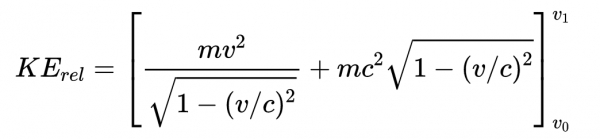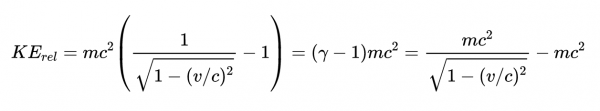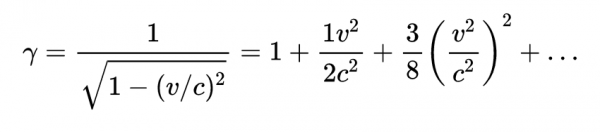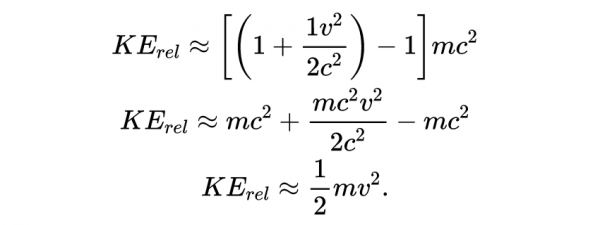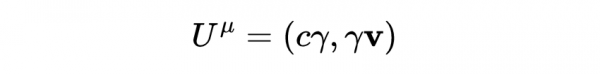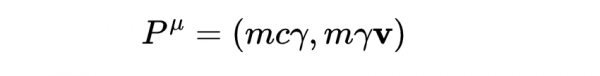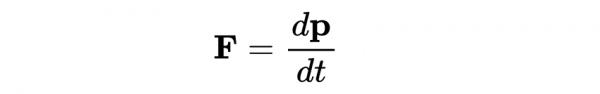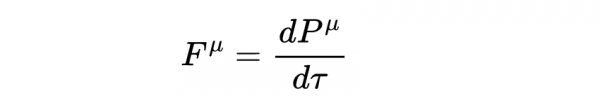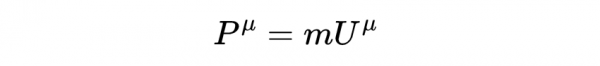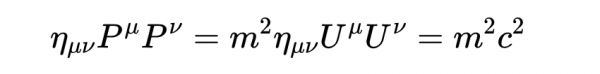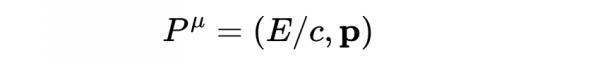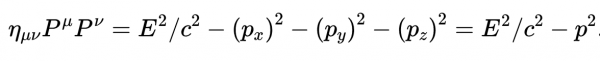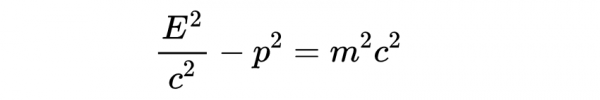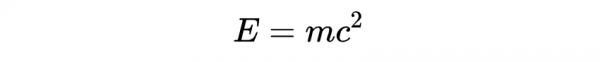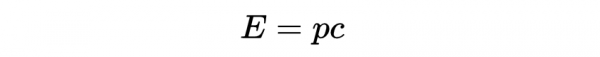我們首先要提到一個物理學中的基本概念,即守恆定律。簡單地說,這些理論表明,無論孤立物理系統如何變化,它的某些特性都是守恆的。能量守恆和動量守恆是我們會遇到的兩個守恆定律。
鐘擺是機械能守恆的一個很好的例子。當鐘擺的球處於最高點時,它暫時靜止,具有最大勢能和零動能。當它透過最低點時,它的勢能為零,動能為最大。但在鐘擺的所有點上,勢能和動能的總和是恆定的,也就是說,機械能守恆。
不變性
一個量在狹義相對論中是不變的,如果它在所有慣性系中有相同的值或相同的形式。“相同值”的不變數指的是不變的物理量(我們已經看到了一些),包括:
- 光在真空中的速度。
- 時空間隔
- 固有時
另一個非常有用的不變物理量是靜止質量m,它是物體或粒子在靜止座標系中的質量。從現在起,每當我們提到質量時,指的是靜止質量,也被稱為不變質量或固有質量。
各種不變物理量之間的關係可以用方程來描述。如果這些方程是不變的(即在所有慣性系中具有“相同的形式”),它們被稱為不變形式或協變(令人困惑的是,協變的用法與我們稍後遇到的“協變向量”的用法不同)。我們知道,物理定律在所有慣性系(相對論原理)中必須採取相同的形式這一假設是狹義相對論的假定之一。現在我們來看一些力學的形式不變定律。
四維速度
我們知道一個引數引數方程可用於定義一條曲線在空間如一個球的路徑。粒子在普通三維歐幾里德空間中的運動路徑可以用t(時間)的三個函式來描述,一個是x,一個是y,一個是z。這三個函式x = f(t), y = f(t), z = f(t)稱為引數方程,並給出一個向量,其分量代表物體在x,y,z方向上的空間速度(或三維速度)。粒子的空間速度是路徑的切線向量,並且有分量
空間速度不使用洛倫茲變換進行變換。然而,在狹義相對論中有一種速度向量是形式不變的,它被稱為四維速度。
考慮四維時空中沿世界線運動的粒子的速度。正如我們所看到的,一個固定在粒子上的時鐘將測量粒子的固有時(我們知道它是不變的),因此使用它作為沿著路徑的引數是有意義的。粒子的四維速度是粒子四位置相對於固有時的變化率。與三速度一樣,四維速度是粒子世界線的切線向量,定義為:
四維速度具有時間分量和空間分量,是一種四維向量,是狹義相對論中一個重要的形式不變數。稍後我們將更詳細地討論四維向量。
為了確定四維速度分量,回想一下,這個方程
給出了與固有時相關的座標時間ΔT,稍作等式變換得到:
使用ct作為時間單位,我們把它改寫成
對固有時求導得到
可以用鏈式法則求出的空間分量
其中
是粒子的普通空間速度,速速分量為
粒子的四維速度由下式給出
在狹義相對論中,兩個四維向量的標量及用閔可夫斯基度規定義為
它在洛倫茲變換下是不變的。四維速度的標量積為
但由於
得到
這顯然是一個不變數。
相對論動量
在牛頓力學中,一個粒子的動量等於這個粒子的質量m乘以它的普通空間速度v:
空間速度有分量
如果牛頓系統(速度遠小於光速)沒有外力作用,動量是守恆的。在狹義相對論中,速度在不同的慣性系之間以複雜的方式變換,因此我們不能使用牛頓動量守恆定律。相反,我們需要引入相對論動量的概念。為了做到這一點,我們用固有時代替座標時間t,並定義相對論動量p為
因為我們已經知道
我們可以把p用座標時間表示為
它會透過洛倫茲變換在不同的慣性系之間變換。重要的是,這意味著和牛頓動量不同,相對論動量在所有慣性系中都是守恆的。
相對論動能
粒子的動能是它由於運動而擁有的能量。在牛頓力學中,質點m以速度v運動的動能定義為使質點從靜止加速到速度v所做的功。做的功W等於力F乘以力作用的距離,也就是
牛頓第二定律將力與質量和加速度聯絡起來F=ma。所以我們可以說所做的功是為
加速度是速度相對於時間的變化率,我們可以把它代入上面的方程來得到
用鏈式法則可以寫成
v_1是粒子在距離s_1處的速度。v_0是粒子距離s_0處的速度。因此積分得到
因為我們把動能定義為使粒子從靜止加速到最終速度v所做的功,而v_0=0並且動能為
因為牛頓動量p = mv,我們可以重寫一下功的計算公式
其中p_0和p_1分別是粒子的初始動量(= 0)和最終動量(=mv_1)。這給了我們一種方法來找到相對論動能。這給了我們一種找到相對論動能的方法,即用相對論動量代替牛頓動量
我們可以先用分部積分法求這個積分
然後,我們需要在第二項上使用代換積分法。首先,提出常數m
讓
把s替換為
得到:
這意味著我們現在可以寫出
然後,右邊項的頂部和底部乘以
讓所有的東西都有一個公分母
讓v_1=v,我們知道粒子從靜止開始加速,因此,我們最終得到了質量為m的粒子以速度v運動的相對論動能的方程:
γ是洛倫茲因子。這看起來和牛頓動能方程很不一樣。然而,使用泰勒定理可以展開洛倫茲因子
因此
在牛頓系統中v<<c,因此忽略平方和更高次項,得到
所以在低速時,相對論動能近似於牛頓動能。
總相對論能量
如果我們重新排列相對論動能的方程,可以寫出
現在我們有了一個方程,它給出了一個粒子在慣性系中的總相對論能量E。總相對論能量由粒子的相對論動能加上第二項mc^2組成(粒子的質能)。它可以在理論上被證明,並且已經在實驗上被證實,在沒有外力作用的情況下,總的相對論能量在所有慣性系中是守恆的,無論質量或動能是守恆的。在高速粒子碰撞中,例如,質量,動能,甚至粒子的總數可能不守恆,但系統的總相對論能量會守恆。
若粒子靜止,則洛倫茲因子減小為1,並且
這是愛因斯坦著名的質能方程,該方程表明,質量和能量在某種意義上是相等的,即使在靜止狀態下,粒子仍然會因為其質量而擁有能量。顯然,c^2是一個很大的數,所以少量的質量產生大量的能量。
四維動量
如果我們把四維速度乘以一個粒子的靜止質量m,就得到另一個四維向量,叫作四維動量:
回想一下四維速度的定義
然後乘以m就得到
而E=γmc^2是相對論總能量,並且p=mγv是相對論動量的方程。我們可以看到mcγ是總相對論能量除以光速,因此四維動量可以重寫為
四動量提供了一個粒子的相對論總能量(它的時間分量)和相對論動量(它的空間分量)的完整描述。Schutz]總結了這一點,他說粒子的四動量是一個向量,在某個座標系中的分量給出了粒子相對於那個座標系的能量和動量。正如我們以後會看到的,所有重要的能量-動量張量,即愛因斯坦場方程的右邊和時空曲率的來源,實際上是四維動量單位面積上的流速的度量。
四維力
牛頓第二運動定律說,作用在物體上的力等於物體動量的變化率
我們可以把它推廣到狹義相對論,定義四維力為四維動量的變化率
它展示了自由粒子如何在彎曲時空中運動。
能量動量關係
四維速度的標量積為:
而四維動量為
因此
但是四維動量的標量積
也可以從
求得,為
把這兩個四維動量標量積的表示式結合起來,我們得到
整理得
對於靜止的質點(即動量為零的質點),這等於
正如我們之前看到的,當我們看相對論總能量時,就是著名的質能方程。光(和其他電磁輻射)可以被認為是一束光子,一種基本粒子。一個“靜止質量”為零的光子,確實有能量和動量。如果我們讓m = 0進來,得到
它描述了光子的能量動量關係。