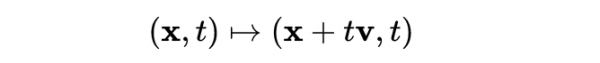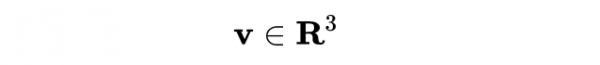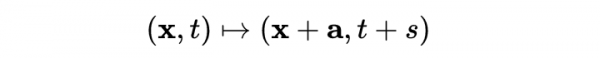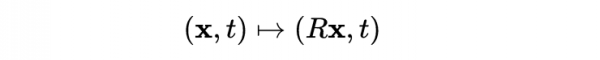常識就是人在十八歲之前形成的各種偏見——愛因斯坦
首先,我們來看看牛頓方程裡沒有什麼。牛頓的方程中不涉及光速c。而光速絕對是愛因斯坦狹義相對論的核心。此外,牛頓力學假定時間和空間是不相關的絕對概念。狹義相對論(只適用於沒有重力的情況)將這兩個量統一成一個稱為時空的單一流體實體。時空中的時間距離和空間距離不再是絕對的,而是取決於觀察者的相對速度。然而,狹義相對論認為,物理定律與任何觀察者的勻速運動無關。
時空圖是將狹義相對論的一些基本性質形象化的一個有用的幾何工具。然後,我們可以在這些見解的基礎上,轉向更代數的方法,引入洛倫茲變換,並努力理解狹義相對論是如何重新表述力學定律的。但首先我們需要介紹一些基本概念。這些都是:時間、時空、事件、參考系、慣性參考系、座標變換、伽利略變、換狹義相對論的兩個假定。
時間
我們已經知道,牛頓力學假設時間是獨立於物理現象的,對所有觀察者來說也是如此。這不是狹義相對論的情況,狹義相對論迫使我們放棄許多關於時間意義的“常識”。例如,同時性不再總是絕對的——空間中分離的兩個事件對一個觀察者來說可能同時發生,但對另一個觀察者來說可能在不同的時間發生。
當我們在狹義相對論中談論時間時,我們不僅僅是在談論讀取的時鐘。相反,我們指的是一種更深刻、更基本的時間概念,即自然過程的內在速率。μ介子是一種微小的亞原子粒子,宇宙射線與地球大氣層的相互作用產生了大量的μ介子。它們的生命週期很短(大約兩百萬分之一秒),很少能活著到達地球表明。大多數能存活下來的原因是,它們以接近光速的速度執行,受到相對論時間膨脹的影響——換句話說,μ介子的“內部時鐘”(不管它是什麼)執行得更慢。
時空
在牛頓力學中,事件是用三維歐幾里德空間加上一個獨立的絕對時間尺度來描述的。在狹義和廣義相對論中,空間和時間都融合成一個單一的四維實體(或連續體),稱為時空。
- 狹義相對論中的時空是平的(平行線不相交)。因此,用笛卡爾座標加上時間座標來描述它是最簡單的。雖然我們用的是笛卡爾座標,但是我們現在已經遠離了我們熟悉的歐幾里德空間。時空是平的,但它不是歐幾里德的,原因很簡單,時空中點之間的距離是用非歐幾里德度規來描述的。
- 相反,廣義相對論的時空是彎曲的,而不是平坦的。
狹義相對論的時空,被稱為閔可夫斯基空間或閔可夫斯基時空,這是以德國數學家赫爾曼·閔可夫斯基的名字命名的,他是愛因斯坦在蘇黎世理工學院的數學老師,1908年,他在一次公開演講中用著名的一句話向世界介紹了時空:
我想在你們面前闡述的關於空間和時間的觀點,是從實驗物理學的土壤中產生出來的。從今以後,單獨的空間和單獨的時間,註定要消逝為純粹的陰影,只有兩者的某種結合才能保持一個獨立的現實。
事件
我們對時空中發生的事情感興趣,我們稱之為事件。事件是在時空中瞬間發生的事情,比如一盞閃爍的燈,或者移動物體上的一個點經過另一個點。時空中的所有事件都用四個座標t,x,y,z來定義。
想象一個粒子在時空中運動。我們可以把粒子的運動看作是一連串事件。如果我們把所有這些事件聯絡起來,我們就會得到一條線來代表粒子在時空中的過程。這條線叫作粒子的世界線。
參考系(參照系)
狹義相對論研究的是相對運動的觀察者如何在時空中測量事件。每個觀測者用來進行測量的座標系稱為參照系。我們用的是簡單的笛卡爾座標,所以我們可以把我們的參照系想象成一系列無限大的笛卡爾座標系在時空中快速移動。我們可以透過使用(x,y,z)座標來確定S中任何事件的空間位置。但我們也需要描述事件發生的時間。因此,我們想象我們的座標系S充滿了無數個有規律間隔的時鐘,所有這些時鐘都是同步的,並以相同的速度執行。要找出事件發生的時間,我們只需查詢與之相鄰的時鐘。
這似乎是一種奇怪的、費力的測量時間的方法。為什麼不想象一個觀察者坐在舒適的椅子上,看到一個遙遠的事件,透過檢視鄰近的超精密鐘錶或手錶來記錄時間。這種情況的問題在於,它並沒有告訴我們事件是什麼時候發生的,只是告訴我們觀察者是什麼時候看到事件發生的,這並不一定是一回事。半人馬座阿爾法星是離地球最近的恆星,距離地球4.4光年。如果它今天爆炸,我們要4.4年才能知道。為了理解時空,我們必須假設我們知道事件發生的確切時間。這就是我們用同步時鐘填充參考系的原因。
它通常有助於避免人類觀察者在一個參照系中進行物理測量的概念。相反,我們可以簡單地將一個參考系定義為一個座標系統,其中每個事件都位於三個空間座標(x,y, z)和一個時間t座標的時空中。
慣性參考系
狹義相對論特別關注均勻運動的參照系,即慣性系。在學習牛頓力學時,我們已經遇到過慣性系,並看到其中的物體遵循牛頓第一定律,即物體將保持靜止或勻速直線運動,除非受到外力的作用。狹義相對論中的慣性系被稱為洛倫茲參考系。
洛倫茲座標系和牛頓慣性座標系一樣嗎?只有在它們都是勻速運動的座標系中物體服從牛頓第一定律。它們在處理引力的方式上有根本的不同:
- 狹義相對論和洛倫茲參考系關注的是在沒有引力的情況下物體和光線的行為。
- 另一方面,牛頓的慣性系,可以包括引力,把它當作另一種力。
洛倫茲座標系只能被精確地構建在平坦時空中,換句話說,這個時空不會因為質能而彎曲。原因之一是引力時間膨脹(在引力場中時鐘執行速度變慢的現象)使得全域性時鐘同步成為不可能。
然而,儘管在引力場中不能建立一個精確的全域性慣性系,但在許多情況下,地球上的區域性參照系是一個有用的慣性系的近似。當討論廣義相對論和等效原理時,我們會看到一個在引力場中自由落體的座標系實際上是一個區域性慣性座標系。
座標變換
我們需要比較觀察者在相對運動中的測量值。假設有一個觀察者O,在S參考系中測量一個事件的時間和空間座標,比如一盞燈忽明忽暗的。我們先搞清楚這是什麼意思。閃光只是時空中發生的一件事。我們可以用無數個參照系來描述這個事件,但我們選擇了一個S。參照系S中的觀測者使用笛卡爾座標和同步時鐘來測量事件,並透過分配四個時空座標t,x,y,z來定義它的位置。
另一個觀測者O'在另一個座標系S'中以相對於S的恆定速度運動,用笛卡爾座標和同步時鐘來測量同一事件,並給它分配了四個座標t', x', y', z'。除非座標系重合,否則t,x,y,z不等於t' ,x', y' ,z'。但是,因為它們都是簡單的笛卡爾座標系,我們希望有一組相當直接的方程,允許我們把座標t,x,y,z,和座標t',x', y',z'聯絡起來。這組方程稱為座標變換。
那麼,對於兩個相對運動的觀察者來說,正確的座標變換是什麼?在狹義相對論出現之前,答案應該是一組非常簡單的方程,即我們現在看到的伽利略變換。
伽利略變換
伽利略變換被用來在兩個參考系的座標之間進行變換,這兩個參考系在牛頓物理學的構造中只有恆定的相對運動。這些變換加上空間旋轉和空間時間的平移形成了非均勻的伽利略群。沒有空間和時間上的平移,群就是同質伽利略群。伽利略群是伽利略相對論作用於空間和時間的四維上的一組運動,形成了伽利略幾何。這就是被動轉化的觀點。在狹義相對論中,齊次和非齊次伽利略變換分別由洛倫茲變換和龐加萊變換代替;相反,龐加萊變換的經典極限c→∞中的群收縮產生了伽利略變換。
伽利略對稱性可以被唯一地寫成,時空的旋轉,平移和均勻運動的組合,設x表示三維空間中的一個點,t表示一維時間中的一個點。時空中的一般點是由一個有序對(x,t)給出的。
速度為v的勻速運動由:
其中:
平移變換由下式給出:
旋轉變換為:
作為李群,伽利略變換群的維數為10。
狹義相對論的兩個假設
愛因斯坦的狹義相對論建立在兩個關於宇宙執行方式的基本假設的基礎上:
- 相對論原理——物理定律在任何慣性參照系中都是一樣的,無論位置或速度如何。
- 在所有慣性參照系中,光速在真空中的恆定值c = 3 × 10^8米每秒。
第一個假設,將伽利略相對論擴充套件到所有的物理定律,並不難接受和理解。第二個假設是令人震驚的。這是一個與我們日常對時間和空間的假設相悖的理論。