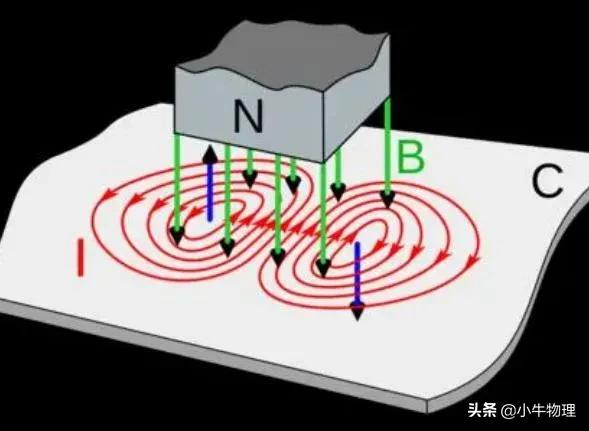
變化的磁場在其周圍空間激發的電場叫渦旋電場,即感生電場。渦旋電場是一種非保守場,其電場線是無始無終的閉合曲線。
感生電動勢源於磁場的變化,跟導體是否構成迴路或迴路是否閉合無關。即使不存在導體或導體迴路,變化磁場周圍的渦旋電場也是存在的,只是這時不存在感應電流。感生電場是一種渦旋電場,渦旋電場會對電荷產生力的作用,電場力與速度均在切線上故電場力在感生電場中做功不為零.
靜電場與感生電場的區別:
(1)產生機理不同,渦旋電場是變化的磁場的產生,而靜電場是電荷產生的。
(2)電場線的特點不同,靜電場的電場線起於正電荷終止於負電荷,是不閉合的;而渦旋電場的電場線沒有起點、終點,是閉合的。
(3)電場力做功不同,渦旋電場線是閉合的,這使得電子在渦旋電場中受到的電場力做的功與其運動路徑有關。比如電子在渦旋電場中沿著導線環運動一週,電場力力做的功W非=ΣF·△S,而在靜電場中電子沿著導線環運動一週,其電場力做功為0。所以在渦旋電場中不能建立“電勢”和“電勢能”的概念。
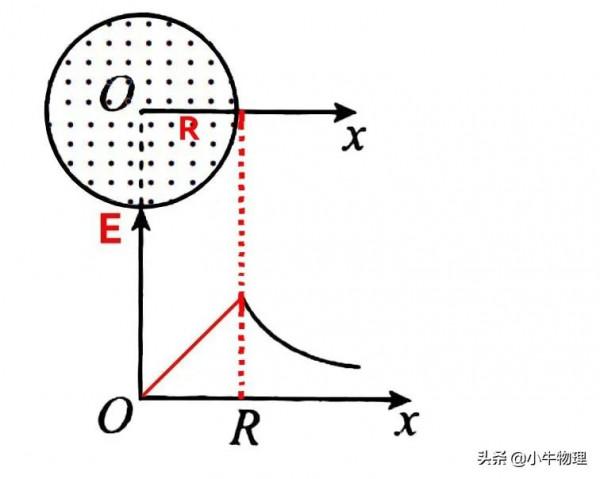
(4)渦旋電場產生的電場強度的分佈有它的特點。
如果以下圖中圓心O為座標原點,向右建立一維座標軸x,在x軸上各處電場強度的大小E與x之間的關係.
求x處的渦旋電場場強,勻強磁場分佈在半徑為R的圓周內.
例題:麥克斯韋電磁理論認為:變化的磁場會在其周圍空間激發一種電場,這種電場與靜電場不同,稱為感生電場或渦旋電場,如圖甲所示。
(1)若圖甲中磁場B隨時間t按B=B₀+kt(B₀、k均為正常數)規律變化,形成渦旋電場的電場線是一系列同心圓,單個圓上形成的電場場強大小處處相等。
將一個半徑為r的閉合環形導體置於相同半徑的電渦旋電場場線位置處,導體中的自由電荷就會在感生電場的作用下做定向運動,產生感應電流,或者說導體中產生了感應電動勢。求:
a.環形導體中感應電動勢E感大小;
b.環形導體位置處電場強度E大小。
(2)電子感應加速器是利用感生電場使電子加速的裝置。它的基本原理如圖乙所示,圖的上部分為側檢視,上、下為電磁鐵的兩個磁極,磁極之間有一個環形真空室,電子在真空室中做圓周運動。圖的下部分為真空室的俯檢視,電子從電子槍右端逸出,當電磁鐵線圈電流的大小與方向變化滿足相應的要求時,電子在真空室中沿虛線圓軌跡運動,不斷地被加速。
若某次加速過程中,電子圓周運動軌跡的半徑為R,圓形軌跡上的磁場為B₁,圓形軌跡區域內磁場的平均值記為B₂(由於圓形軌跡區域內各處磁場分佈可能不均勻,B₂即為穿過圓形軌道區域內的磁通量與圓的面積比值)。電磁鐵中通有如圖丙所示的正弦交變電流,設圖乙裝置中標出的電流方向為正方向。
a.在交變電流變化一個週期的時間內,分析說明電子被加速的時間範圍;
b.若使電子被控制在圓形軌道上不斷被加速,B₁與B₂之間應滿足B₁=B₂/2的關係,請寫出你的證明過程。
例題:如圖甲所示,在圓柱形區域記憶體在一方向豎直向下、磁感應強度大小為B的勻強磁場,在此區域內,沿水平面固定一半徑為r的圓環形光滑細玻璃管,環心O在區域中心.一質量為m、帶電荷量為q(q>0)的小球在管內沿逆時針方向(從上向下看)做圓周運動.已知磁感應強度大小B隨時間t的變化關係如圖乙所示,其中T₀=2πm/qB₀設小球在運動過程中電荷量保持不變,對原磁場的影響可忽略.
(1)在t=0到t=T₀這段時間內,小球不受細管側壁的作用力,求小球的速度大小v₀.
(2)在豎直向下的磁感應強度增大的過程中,將產生渦旋電場,其電場線是在水平面內一系列沿逆時針方向的同心圓,同一條電場線上各點的場強大小相等.試求t=T₀到t=1.5T₀這段時間內細管內渦旋電場的場強大小E及電場力對小球做的功W.