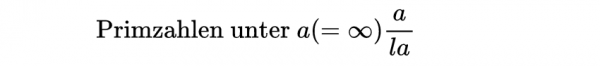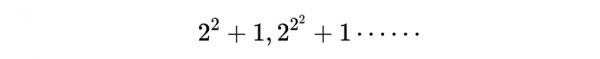卡爾·弗里德里希·高斯(1777~1855)是一個神童。19歲差一個月的他作出了一項非凡的發現。2000多年以來,人們知道如何用直尺和圓規作等邊三角形和正五邊形(還有其他的正多邊形,其邊數是2、3、5的倍數),但不知道如何作出邊數為素數的正多邊形。高斯證明,正七邊形也能用直尺和圓規作出。
- 高斯日記
高斯透過寫日記來紀念他的發現,在接下來的18年裡,他在這本日記中記下了他的很多發現。他還是一個學生的時候就獲得了很多成功。其中有一些是對尤拉、拉格朗日及其他18世紀數學家們已經證明的定理的重新發現;有很多是新發現。在他學生時代的更重要的發現中,我們可以挑出最小平方法、數論中二次互反律的證明,以及他對代數基本定理的研究。他獲得了博士學位,學位論文的標題是《關於所有含一個變數的有理代數整函式都能分解為一次或二次實因子的定理的新證明》。這是他一生中所發表的代數基本定理的4個證明當中的第一個,在這篇論文中,高斯強調了在證明這個定理的過程中證實至少有一個根的重要性。下面的說明可以顯示他的思路。
我們可用圖示的方法解方程
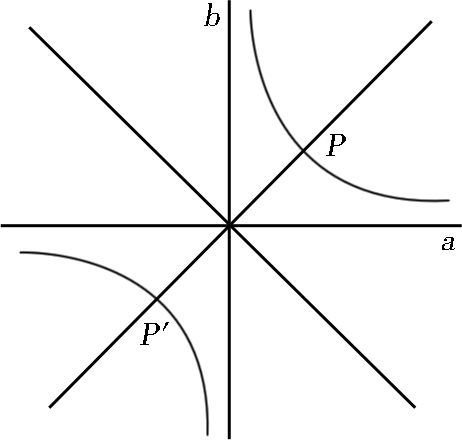
證明存在一個複數值z=a+bi滿足這個方程。用a+bi取代z,並分開方程中的實數部分和虛數部分,我們就得到a^2-b^2=0和ab-2=0。把a和b解釋為變數,並在同一座標系中畫出這些函式,一個座標軸代表實數部分a,另一個座標軸代表虛數部分b,我們就有了兩條曲線;一條由直線a+b=0和a-b=0構成,另一條由等軸雙曲線ab=+2構成。
很顯然,這兩條曲線有一個交點P在第一象限。我們應該特別注意,第一條曲線的一條分支沿著θ=1π/4和θ=3π/4的方向離開原點;第二條曲線的一條分支漸近地向著θ=0π/4和θ=2π/4的方向移動;交點在最後兩個方向θ=0和θ=π/2之間。這個交點的a和b的座標是方程z^2-4i=0的一個解的實數部分和虛數部分。假如我們最初的多項式方程是三次而不是二次,則一條曲線的一根分支就會趨近於θ=1π/6和θ=3π/6的方向,另一條曲線就會趨近於θ=0π/6和θ=2π/6的方向。在每一種情況下這些分支都是連續的,因此,它們一定要相交於θ=0至θ=π/3之間的某個地方。
對於一個n次方程來說,一條曲線的一根分支有漸近方向θ=1π/2n和θ=3π/2n,而另一條曲線的分支有漸近方向θ=0π/2n和θ=2π/2n。這些分支必定相交於從θ=0至θ=π/n之間,這個交點的a和b的座標,就是滿足這個方程的複數的實數部分和虛數部分。因此我們看到,不管一個多項式方程的次數是幾,它必定至少有一個複數根。我們會注意到,高斯依靠這些曲線的圖示來證明它們相交。承認這個結果,多項式方程可以分解為一次或二次實因子也就得到了證明。
數論
高斯在他還是哥廷根大學的一名學生的時候,就開始撰寫一部重要的數論著作——《算術研究》,是數學文獻中的偉大經典之一,在他的博士論文透過兩年之後出版。此書由7個部分組成。前4個部分本質上是對18世紀數論的濃縮重構。討論的基本原則是同餘和剩餘類的概念。第5部分致力於二元二次型理論,特別是形如
的方程的解的問題;這一部分所發展出來的技術,成了後來一代代數論學家所做的大量工作的基礎。第6部分由各種不同的應用所組成。最後一部分起初吸引了最多的關注,處理的是次數為素數的割圓方程的解。
高斯把勒讓德在兩年前發表的二次互反律稱作黃金定律。在後來的作品中,高斯試圖得出同餘式x^n=p(modq)對於n=3和4的類似定理;但對這兩種情況,他發現有必要把“整數”這個詞的意義擴大到包括所謂的高斯整數,亦即形如a+bi的整數,式中,a和b都是整數。高斯整數構成了一個整環,像實整數整環一樣,但更一般。可整除性的問題變得更復雜,因為5不再是一個素數,可分解為兩個“素數”1+2i和1-2i的乘積。事實上,任何形如4n+1的實素數都不是“高斯素數”,而形如4n-1的實素數依然是一般化意義上的素數。在高斯的《算術研究》中,包括了算術基本定理,它是在高斯整數的整環中繼續有效的基本原理之一。事實上,任何一個因子分解是唯一的整環今天都被稱作高斯整環。《算術研究》的貢獻之一是下面這個定理的證明,這個定理自歐幾里得時代以來就被人所知:
任何一個正整數都可以用一種、且只能用一種方式表示為素數的乘積。
高斯關於素數的發現,並沒有全都包含在《算術研究》中。在他還是一個14歲的孩子時,高斯就在一張對數表的背面,用德文寫下了這樣一行隱晦的文字:
這行文字說的是一個著名的素數定理:小於給定整數a的素數的個數在a無窮遞增時趨近於a/lna。
正如我們已經看到的那樣,勒讓德曾經接近於預先發現這個定理;但奇怪的是,正如我們所推測的那樣,高斯寫下了這個定理,但他一直對這個巧妙的結論保守秘密。我們不知道他是否證明了這個定理,甚至也不知道他何時寫下了這個定理的陳述。素數的分佈對數學家有著強烈的吸引力。
1845年,當高斯已經是個老人的時候,巴黎的一位教授約瑟夫·L.F.貝特朗提出了這樣一個猜想:如果n>3,那麼,在n與2n(或者更準確地說是2n-2)之間至少包括一個素數。這個猜想被稱作貝特朗公設,在1850年被聖彼得堡大學的帕夫努蒂·切比雪夫所證明。切比雪夫作為他那個時代首屈一指的俄國數學家,是羅巴切夫斯基的競爭對手,他後來成了法蘭西科學院和英國皇家學會的外籍院士。切比雪夫明顯不知道高斯論述素數的作品,他能夠證明,如果π(n)(lnn)/n在n無窮遞增時趨近於一個極限,那麼,這個極限必定是1;但他不能證明一個極限的存在。直到切比雪夫去世兩年之後,一個證明才廣為人知。
關於素數的個數和分佈的問題,從歐幾里得時代迄至今日,讓很多數學家神魂顛倒。有一個定理,高斯本人在《算術研究》中給出了一個驚人的例項,說明了這樣一個事實:素數的屬性甚至以最出人意料的方式侵入了幾何學的領域。
高斯在《算術研究》的結尾部分,收入了他在數學領域作出的最早的重要發現:正七邊形的作法。他透過證明無窮多種可能的正多邊形中哪些能作出、哪些不能作出,從而把這一課題帶向了其邏輯結果。一般性的定理,比如高斯眼下所證明的,遠比一個特例更有價值,不管這個特例多麼壯觀。我們應該還記得,費馬曾經相信,形如
- 費馬數
的數是素數,尤拉後來證明這個假說是錯誤的。高斯已經證明了,正17邊形是可以作出的,問題自然出現了:正257邊形和正65537邊形是否可以用歐幾里得的工具作出。在《算術研究》中,高斯對這個問題的回答是肯定的,他證明了,只要N是
的形式(式中,m是任一正整數,pn是不同的費馬素數),那麼,正N邊形就可以做出。這個問題還剩下一個方面高斯沒有回答,而且迄今為止沒有人作出回答,這就是:
費馬素數的個數是有限還是無限?
我們已經知道,對於n=5、6、7、8和9來說,費馬數不是素數,但看來很有可能,有且只有5種可以用直尺和圓規作出的邊數為素數的正多邊形,其中兩種在古代已經知道,另外三種是高斯發現的。有一個高斯很讚賞的人,就是柏林的數學教師費迪南德·戈特霍爾德·愛森斯坦,他補充了一個關於素數的新猜想,當時,他大膽提出了一個迄今為止尚未得到證明的想法:形如
等等的數是素數。據說,高斯曾發表這樣的評論:“只有三個劃時代的數學家:阿基米德、牛頓和愛森斯坦。”可惜愛森斯坦在不到30歲的時候便去世了。
高斯的《算術研究》一直處於沉睡狀態,直至1820年代,C.G.J.雅可比和狄利克雷第一次揭示出,一些更深刻的結果正是源自於這部著作。
高斯對天文學的貢獻
1801年1月1日,巴勒莫天文臺臺長喬賽普·皮亞齊發現了新的小行星穀神星;但幾個星期之後,這顆小行星便看不見了。高斯相信,自己有非同尋常的計算能力,還有最小平方法的額外優勢,於是他接受了挑戰,要從這顆行星少量記錄在案的觀測資料中,計算出其執行軌道。為了完成從有限觀測資料中計算執行軌道的任務,他設計出了一種方法,被稱作高斯法,至今依然被用來追蹤衛星。結果是一次引人矚目的成功,這顆行星在這年年底被重新發現,跟他計算出的位置非常接近。高斯的軌道計算吸引了世界各國天文學家的關注,很快就使他在德國數學科學家中贏得了突出聲望,當時,他們當中大多數人都從事天文學和測地學活動。1807年,他被任命為哥廷根天文臺臺長,他保有這個職位將近半個世紀。兩年後,他論述理論天文學的經典著作《天體運動論》出版。這本書為軌道計算提供了一份清晰的指導,到他去世的時候,已經被翻譯成英文、法文和德文。
然而,軌道計算並不是高斯為自己贏得名聲併為後代鋪平道路的唯一的天文學領域。19世紀的頭十年裡,他的很多時間花在了研究攝動問題上。在高斯的好友、希·威爾海姆·奧伯斯於1802年重新發現了小行星智神星之後,攝動問題成為天文學家關注的焦點。智神星的偏心率相對較大,尤其受到其他行星(像木星和土星)的引力的影響。確定這些引力的影響,是n體問題(尤拉和拉格朗日曾對n=2或3的情況進行過研究)的一個特例。
高斯從早年起就有意識地追蹤這兩位天才的足跡,對他來說,找出最近似解法這個難題尤其引人入勝。儘管他認為,他的成果當中只有一部分達到了公開發表的質量,但他對這個問題的研究,不僅導致了一些天文學論文,而且還有兩篇經典論文,一篇是無窮級數,另一篇是數值分析的一種新方法。前一篇論文在1812年提交給了哥廷根協會,致力於研究超幾何級數。因為這篇論文中所提出的收斂準則,常常被認為是開闢了數學分析嚴謹性的新時代。然而,應該指出的是,對收斂性的更深刻的理解,並沒有阻止高斯和當時其他偉大的數學家在解決物理問題時使用發散級數,只要他們認為自己能夠“有把握地”這樣做就行。
微分幾何的肇始
高斯在1827年開始的幾何學分支被稱作微分幾何,它大概更多地屬於分析學,而不是屬於傳統的幾何學領域。自牛頓和萊布尼茨時代以來,人們一直把微積分應用於二維空間的曲線研究,在某種意義上,這項工作構成了微分幾何的雛形。尤拉和蒙日把這一應用擴大到了對曲面的解析研究;因此,他們有時候被認為是微分幾何之父。然而,直到高斯的經典論著《曲面的一般研究》出版,才有了一部完全專注於這一課題的綜合性著作。粗略說來,正統幾何學感興趣的是一個給定幾何圖形的整體,而微分幾何關注的是一條曲線或一個曲面在其上的一點的鄰近區域的屬性。在這個方向上,高斯透過定義一個曲面在一點上的曲率———“高斯曲率”或“總曲率”———從而擴充套件了惠更斯和克萊羅在一條平面曲線或非對稱曲線的曲率上所做的工作。
如果透過一個良態曲面S上的一點P作S的法線N,則透過N的平面束將會跟曲面S相交於一簇平面曲線,其中每一條曲線都有一個曲率半徑。有著最大麴率半徑和最小曲率半徑(R和r)的曲線的方向,被稱作S在點P上的主方向,它們始終互相垂直。R和r的量值被稱作S在點P上的主曲率半徑,S在點P上的高斯曲率被定義為K=1/rR。量值為
被稱作S在點P上的平均曲率。高斯給出了根據曲面對於不同座標系(曲線座標系和笛卡爾座標系)的偏導數的條件求高斯曲率K的公式;他還發現了一些關於在曲面上畫出的曲線簇(比如測地線)的屬性的定理,就連他也認為是“引人注目的定理”。
高斯透過使用尤拉提出的一個曲面的引數方程,開始對曲面的處理。高斯證明了,一個曲面的屬性僅依賴於E、F和G。
這導致了很多的結果。特別是,它使得我們很容易說,曲面的屬性是恆定的。正是在高斯的這一工作的基礎上,黎曼及後來的幾何學家轉變了微分幾何的主題。
高斯的晚期工作
高斯晚期研究貢獻了兩篇重要的短文:一篇是“代數中哈里奧特定理”的證明,另一篇包含了高斯的最小約束原理。歷史學家常常引用第一篇論文(發表於1832年),因為它包含了高斯的複數的幾何表示。這篇論文作為整體的重要性在於下面這個事實:它指出了一條道路,可以把數論從實數擴大到複數領域,甚至更遠。正如上文已經指出的那樣,這在數論領域後來研究者的工作當中是至關重要的。
高斯在他生命的最後20年裡,只發表了兩篇有數學意義的重要論文。一篇是他對代數基本定理的第四個證明,這個證明是他在1849年自己的博士週年紀念的時候釋出的,距離他發表第一個證明已經時隔50年。另外是一篇關於位勢理論的很有影響論文,發表於1840年。地磁學問題在19世紀30年代和40年代早期佔了他的很多時間;在30年代晚期,他還投入了不少時間研究跟重量和度量有關的問題。他生命中最後十年的大部分出版物跟天文臺的工作有關;涉及到課題有:新發現的小行星、對海王星的觀測。
1855年2月23日,高斯死於心臟病發作。