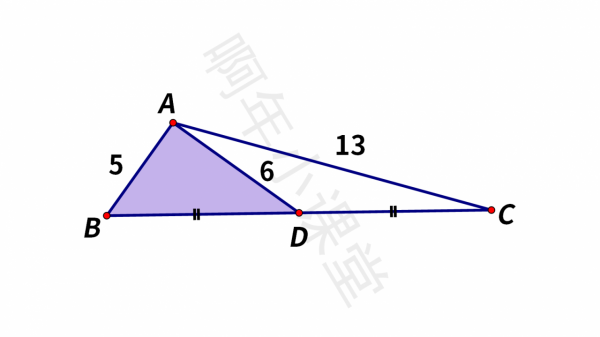
如圖,在△ABC中,AB=5,AC=13,BC邊上的中線AD=6,求△ABD面積。這道題怎麼做呢?
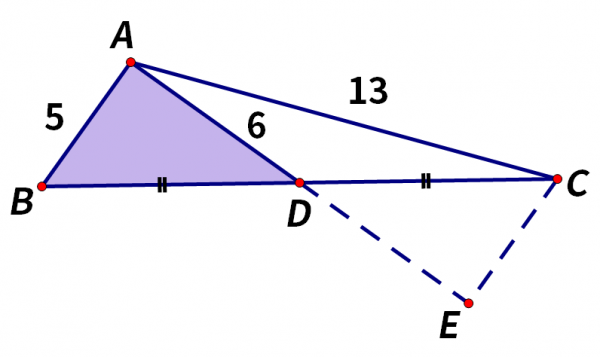
這裡分享一種作輔助線的方法,倍長中線法。
延長AD,使得DE=AD,接著再連線CE。
我們看到三角形ABD和三角形ECD。
在三角形ABD和三角形ECD中,
AD=ED,
∠ADB=∠EDC(對頂角相等),
BD=CD,
由邊角邊證全等,可以得到三角形ABD和三角形ECD全等。
三角形ABD和三角形ECD全等,
EC=AB=5,ED=AD=6,
AE=AD+ED=12。
在三角形ACE中, AC=13,EC=5,AE=12,
AC²=EC²+AE²,
由勾股定理的逆定理可得,三角形ACE是直角三角形,∠AEC=90°。
因為三角形ABD和三角形ECD全等,所以∠BAD=∠CED=90°,
三角形ABD是直角三角形,
三角形ABD的面積=AB×AD÷2=5×6÷2=15。
以上就是這道題的解法,除此之外你還有其他的方法嗎?可以在評論區留言~