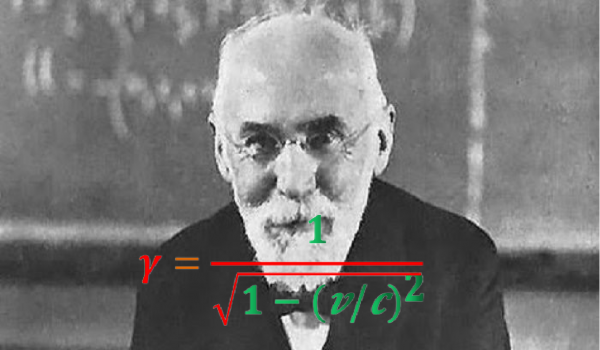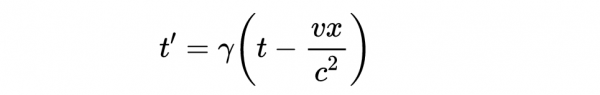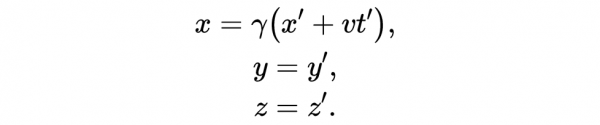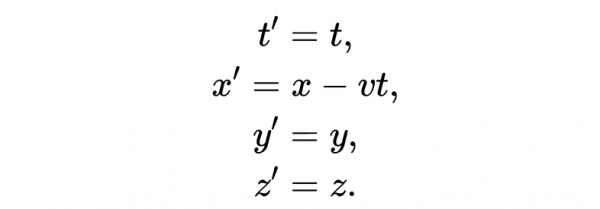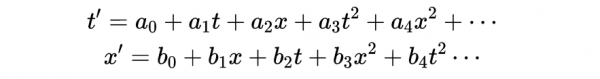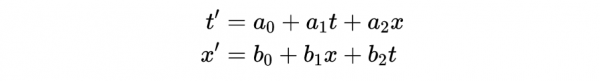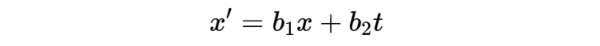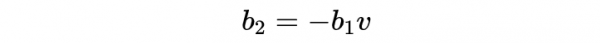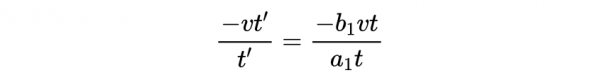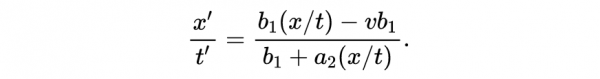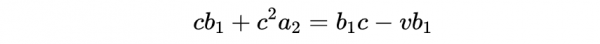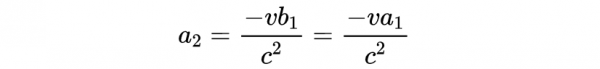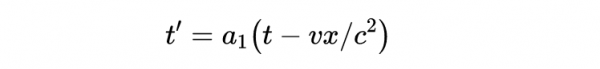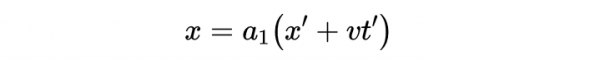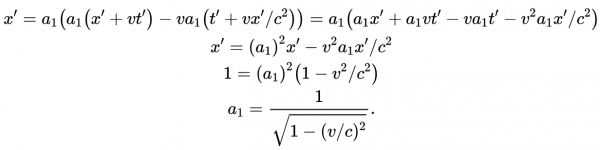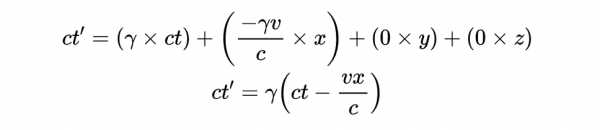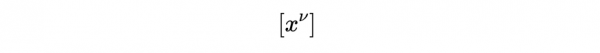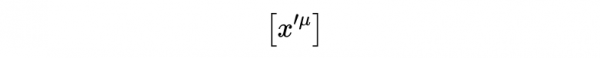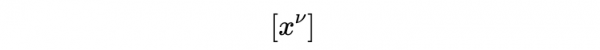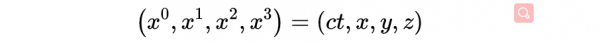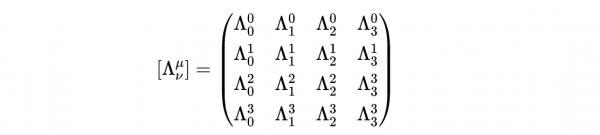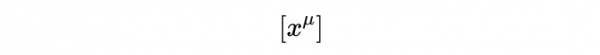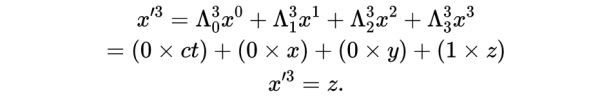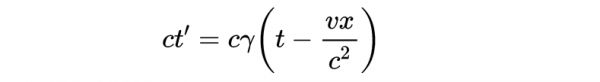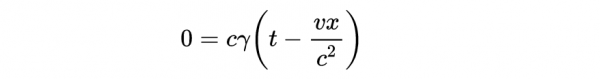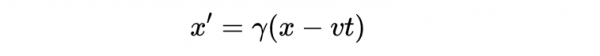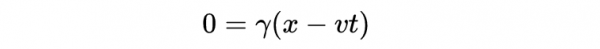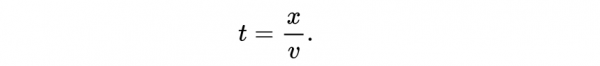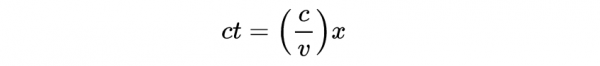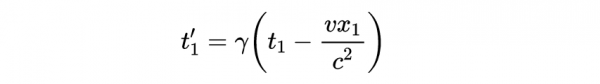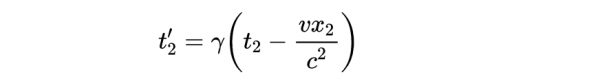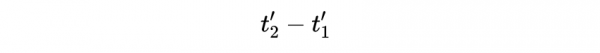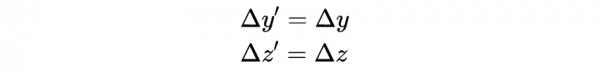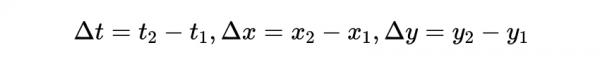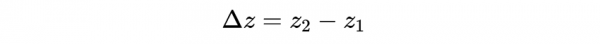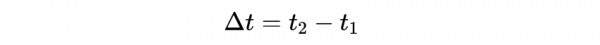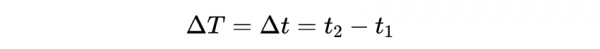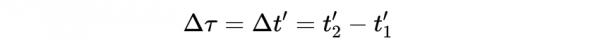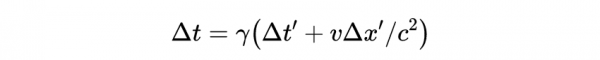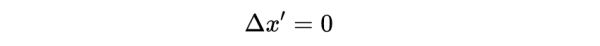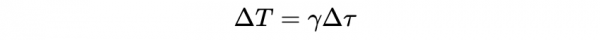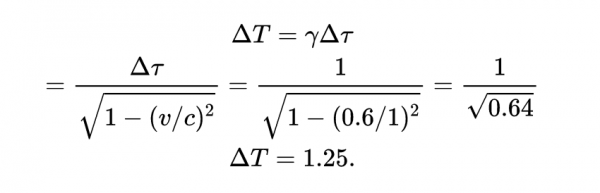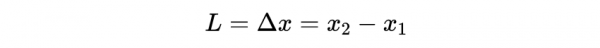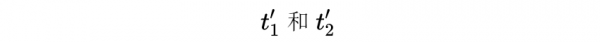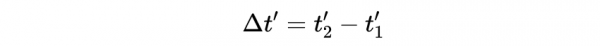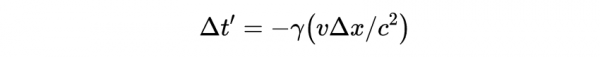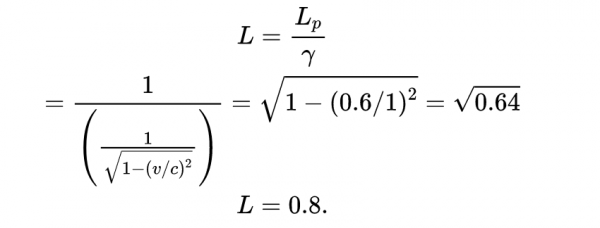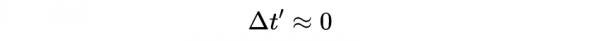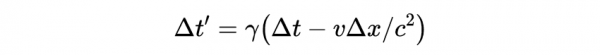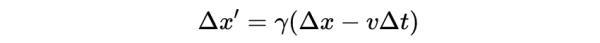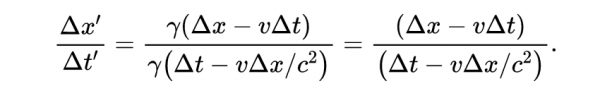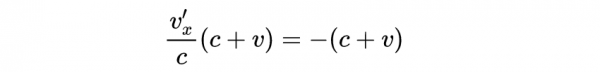透過觀察時空圖從數學角度理解因果關係和狹義相對論中最重要的間隔不變性定理,我們已經對時空的奇特性質有了一些瞭解,我們需要發展出一個精確的代數公式,來說明不同慣性觀測者的座標如何變化。我們用一組叫作洛倫茲變換的方程來做這個,該方程首先由荷蘭物理學家亨德里克·洛倫茲推匯出來。
讓我們重申一下我們正在做的事情的要點。事件t,x,y,z在時空中是由一個觀測者用他的座標系描述的。慣性系S'中的另一個觀察者O'用他的座標系描述了相同的事件t', x',y',z'。基本的問題是:座標t,x,y,z和t',x',y',z'有什麼關係?和往常一樣,我們假設兩個座標系都是標準構型。
我們已經知道,如果第二個假設是正確的(光速c對所有慣性觀測者來說都是恆定的),就不能用伽利略變換來比較一組座標和另一組座標。相反,我們使用洛倫茲變換。稍後我們將推導洛倫茲變換。現在我們只給他們表示式。
我們從洛倫茲因子開始,用希臘字母γ表示,其中:
ν是另兩個座標系統的相對速度,c是光速。從這個方程的結構中看出,如果ν大於等於c,就會出現零或負數的平方根,γ的表示式變得沒有意義,這表明c是自然界中可能的最大速度。因此我們只考慮v小於c的情況。
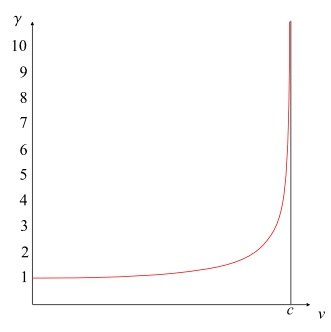
現在我們看到,當ν≠0時,洛倫茲因子總是大於1。對於正常的日常速度,它會非常非常接近1,下圖顯示了洛倫茲因子隨速度ν的變化情況:
- 洛倫茲因子作為速度的函式。
對於不同的ν/c值,洛倫茲因子的值如下:
|
ν/c |
γ |
|
0.000 |
1.000 |
|
0.100 |
1.005 |
|
0.300 |
1.048 |
|
0.500 |
1.155 |
|
0.700 |
1.400 |
|
0.900 |
2.294 |
|
0.990 |
7.089 |
|
0.999 |
22.366 |
洛倫茲因子代入洛倫茲變換,得到座標t',x' ,y',z'的值。
洛倫茲變換是:
洛倫茲反變換(給出座標t, x, y, z的值)是:
注意,當ν<<c時,洛倫茲變換近似於伽利略變換:
觀察洛倫茲變換的一個有用的方法是,它允許我們在時空圖上,校準第二座標系的軸。
推導洛倫茲變換
我們現在可以推導洛倫茲變換。記住,我們試圖找到事件在兩個慣性系S和S’中的座標之間的關係,S’以ν相對於S的速度運動。我們假設兩個座標系都是標準構型(所以我們可以忽略y和z座標,而專注於t和x座標)。
- 式1
牛頓第一定律適用於所有的慣性系,也就是說這些系統不能加速,因此我們省略平方項及更高次冪項,得到:
- 式2
現在我們需要找出未知常數:
因為座標系是標準構型,我們知道當原點與t' = t = 0和x' = x = 0重合時。因此它必須有:
我們現在可以說:
- 式3
- 式4
在時間t之後,座標系S'(由x' = 0給出)的原點在座標系S中移動了距離x = vt,因此我們可以將上式改寫為:
也就是:
用式4除以式3,並把上式帶入b_2得到:
- 式4
在時間t'之後,座標系S(由x = 0給出)的原點在座標系S'中的x' = -vt'處。因此可以將式4重寫為:
得到a_1=b_1,帶入式4得到:
- 式5
現在回想一下,狹義相對論的一個假設是,真空中的光速,在所有的慣性參照系中,都有相同的c值。這意味著,如果一束光從原點沿x軸正方向發射(ct = 0, x = 0),它的速度為c = x'/t'以及c = x/t,我們可以將其代入式7得到:
整理得:
因為a_1=b_1,所以有:
重寫式3為:
- 式6
因此由式4,得到:
- 式7
現在我們需要用t和x表示式6和式7。實際上,這意味著我們已經從一個在座標系S中的觀察者改變了觀察座標系S',成為座標系S'的觀察者,觀察座標系S,因此座標系S沿著- x'軸遠離我們,所以我們需要用-ν代替ν來得到:
- 式8
- 式9
我們快成功了。現在將式8和式9代入式7得到:
我們已經證明了這個常數a_1就是洛倫茲因子γ。
洛倫茲變換矩陣形式
洛倫茲變換的另一種表達方式是矩陣形式:
- 式10
右邊的4 × 4矩陣叫做洛倫茲變換矩陣。
除以c得到:
也就是t'的洛倫茲變換。類似地,我們透過將右邊兩個矩陣相乘得到x' ,y'和z'。當我們討論廣義相對論中的向量和張量時我們會更詳細地研究變換矩陣。用指數表示法,把洛倫茲變換矩陣寫成更緊湊的形式:
- 式11
其中:
表示式10左側的列向量,
是洛倫茲變換矩陣,
是式10右邊的列向量,指數μ和ν取0到3的值,所以分量
是:
分量
是:
變換矩陣的分量是:
其中μ指的是行,ν指的是列。
這個量:
是“四位置”(我們第一個關於四向量的例子),它用ct,x,y,z四個分量來描述時空中的事件或位置。
嚴格地說,式11中的方括號意味著我們引用的是矩陣。我們可以把這個方程寫成矩陣的分量的形式:
根據愛因斯坦求和約定,例如,μ=3時,那麼
從現在開始,我們將經常使用這種簡寫的指數表示法。
第二個觀察者
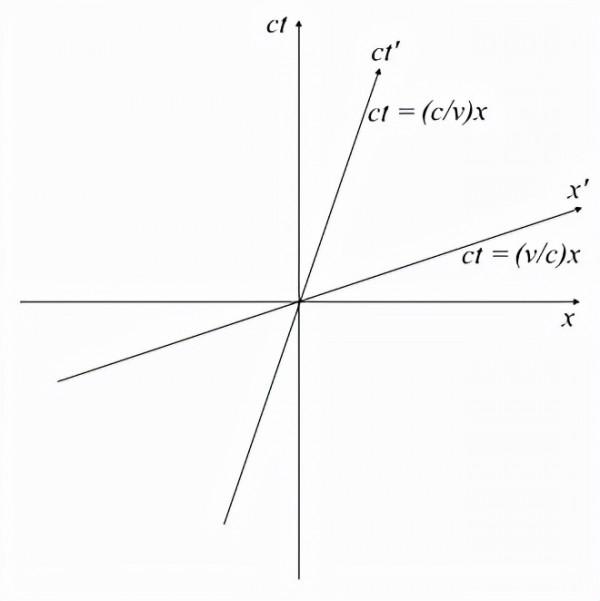
在上一篇文章中,我們利用光速c的恆常性在座標系S'的時空圖上構造第二個慣性座標系S的座標線ct'和x'。我們現在可以用洛倫茲變換用代數方法描述這些軸。
ct'的洛倫茲變換為:
- 式12
我們要求出x'軸的方程,也就是ct' = 0的直線。式12則為:
得到:
- 式13
也就是x'軸的方程。類似地,x'的洛倫茲變換是:
我們要求出ct'軸的方程,也就是x' = 0的直線。因此我們可以這樣寫:
得到:
乘以光速得:
- 式14
這是ct'軸的方程。
- 用洛倫茲變換求第二個觀測者的座標線。
間隔轉換規則
洛倫茲變換告訴我們事件(即時空中的單點)是如何從一個座標系轉換到另一個座標系的。如果在時空中有兩個事件,那麼相應的時間座標和空間座標之間就會有差異。正如我們已經注意到的,這些差異Δt, Δy,Δx,Δz稱為間隔。
瞭解時空間隔是如何變換的是非常有必要的。我們推匯出區間變換的規則如下。對於標記為1和2的兩個事件,洛倫茲變換為:
- 式15
- 式16
如果我們能知道:
和
我們就知道了這些間隔的變換規則
- 式17
- 式18
其中:
類似地,使用反洛侖茲變換,得到:
- 式19
- 式20
固有時和時間膨脹
在前面的文章,我們討論不變雙曲線的性質時,提到了時間膨脹的反直覺現象。現在我們用洛倫茲變換更仔細地觀察時間膨脹。
到目前為止,我們一直使用的是座標時間,座標時間指的是一個遙遠的觀察者用自己的時鐘測量的時間。正如我們所看到的,每個慣性系都有自己的時間座標(時空圖上不同的時間軸)。座標時間因觀測者的不同而不同。但是觀察者用他們自己的時鐘測量的時間呢?這是一個不變的時間度量,稱為固有時,我們可以用它來計算時間膨脹。
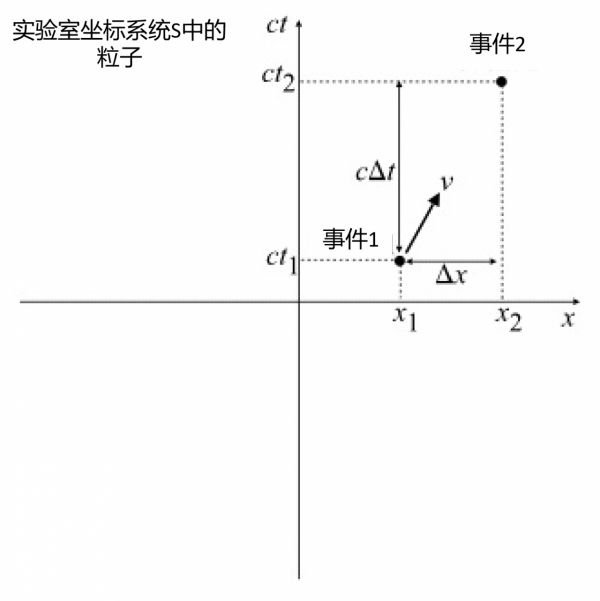
- 在實驗室系統S中運動的粒子
假設我們在一個實驗室裡研究亞原子粒子,它們在正x方向上以恆定速度ν運動。假設我們正在研究的粒子是短命的,它是在一個我們稱之為事件1的時空點上產生的,然後在另一個標記為事件2的點上衰變。
我們是觀察者O,如果,事件1和事件2發生,那麼我們測量粒子的壽命:
粒子移動的距離是:
但是還有一個很明顯的參考系需要考慮,那就是S'座標系中的觀察者O',和粒子一起運動。這叫做粒子的靜止座標系。
你可以想象一下這樣的場景,你正在駕駛一輛汽車,在你旁邊的副駕駛座位上有一個購物袋。購物袋等價於粒子,你是觀察者O',而汽車是袋子的靜止座標系S'。站在路邊的人們會看到購物袋以每小時70英里的速度從他們身邊呼嘯而過。但對你來說,這個袋子是固定的。
- 靜止座標系S'中的粒子
上圖顯示了靜止座標系S'下的粒子。就像購物袋相對於你是靜止的,所以根據觀察者O',粒子在產生和衰變之間不會在空間上移動。
在狹義相對論中,固有時是觀察者在其靜止座標系中測量的時間。固有時用希臘字母tau(τ)表示。在我們的例子中,我們可以想象一個精確的時鐘綁在粒子上。這是難以想象的,所以考慮粒子的自然“內部時鐘”可能會更容易,這種未知的機制最終會對粒子說,“恐怕時間到了。”內部時鐘記錄的時間是粒子的固有時間。
對於粒子,事件1和事件2之間的固有時為:
現在我們有兩種測量粒子壽命的方法:(1)座標時間:
我們用實驗室裡的儀器進行測量,以及(2)固有時:
這是透過粒子自身的內部時鐘來測量的。我們可以用間隔變換規則將兩者聯絡起來:
因為:
所以:
另一種觀察這個過程的方法是,一個過程需要一個特定的固有時,而另一個相對於靜止座標系運動的觀察者所測量到的持續時間更長,即運動的時鐘執行緩慢。這就是我們在上一篇文章中討論的時間膨脹現象。
黑色箭頭TD是由O'沿著ct'軸測量的B = 1事件的時間膨脹ΔT。我們如何計算黑箭頭TD的長度?我們發現事件B的固有時由O'測得:
長度收縮
我們已經用時空圖來探索長度收縮的現象。現在,我們更仔細地看看使用洛倫茲變換的長度收縮。
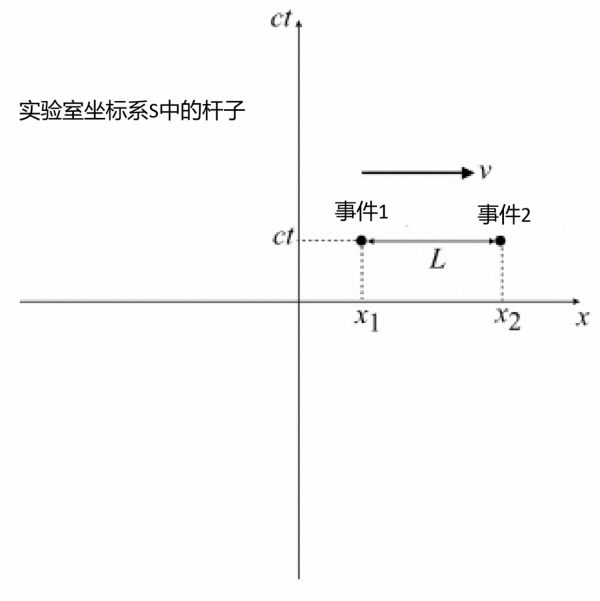
- 在實驗室座標系中的杆子(棒)
上圖顯示了在實驗室慣性座標系S下,杆以速度ν沿x軸縱向運動。杆的長度L可以透過假設杆的一端(對應於事件1)和另一端(對應於事件2)來測量。杆子的長度將為:
現在,就像我們對時間膨脹所做的那樣,考慮杆處於靜止座標系S’中,杆沿x’軸靜止,如上圖所示。我們知道事件1和2仍然會發生在杆的末端,但我們不知道這些事件發生的時間。如果,在靜止座標系中,事件1和事件2分別發生,觀察者O'將測量桿的長度(稱為杆的固有長度):
因為我們不知道
因此也不知道:
但這不是問題,因為我們可以使用間隔轉換:
把表示式帶入:
得到:
回憶一下,黑色箭頭LC是由O觀察到的長度收縮L,長度OD = 1由O'沿著x'軸測量。我們如何計算黑箭頭LC的長度?
利用上式,其中L_p=1,得到:
同時性的終結
我們在看時空圖時發現,事件的同時性可以依賴於觀察者的參照系。我們可以用間隔變換規則來進行代數表示
如果在座標系S中兩個事件同時發生,那麼:
只要它們不發生在同一點,我們就可以說:
其中L為距離Δx。這個方程是同時性相對性的代數公式。我們可以看到,對於非常低的速度(v<<c),有:
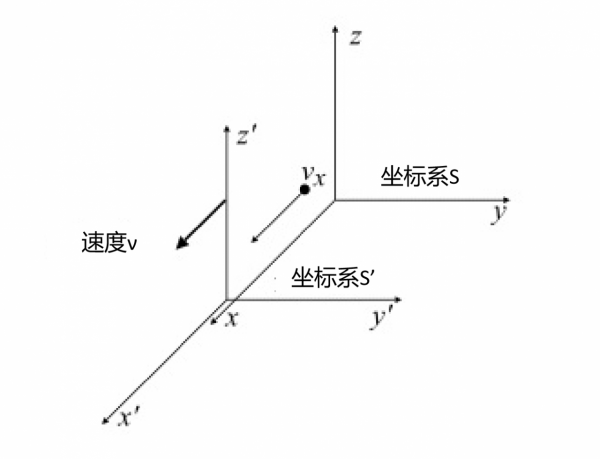
速度變換
上圖顯示了標準構型的兩個慣性系,一個物體沿座標系S的x軸以速度v_x運動。根據座標系S'中的觀察者,物體的運動速度v'是多少?對於這例子,伽利略的答案將是:
現在我們用洛倫茲變換來解決這個問題。我們可以使用兩個間隔轉換規則:
和
描述在座標系S的x軸上發生的兩個事件,如果我們用第二個方程除以第一個,得到:
接下來,我們將右邊的頂部和底部表示式除以Δt:
如果我們讓x軸上的兩個事件越來越近,最終,當Δx和Δt接近0時,得到這兩個事件的瞬時速度。上式則為:
這個方程告訴我們什麼?
首先,如果和v_x和v,與光速相比非常小,就會得到伽利略速度。其次,讓我們考慮一下,如果物體現在是一束向座標系S'相反方向移動的光線,會發生什麼?在S'座標系下,觀測者測量光線的速度有多快?
狹義相對論的第二個假定指出,在所有慣性參照系中,光速在真空中的值c = 3 × 10^8 米每秒。根據第二個假設答案應該是-c。但是速度變換給了我們什麼?
把v_x=-c帶入速度變換(上式)方程中,得到:
整理得到:
那麼:
因此:
這正是第二個假設所要求的。正如預期的那樣,我們也可以看到這與座標系S和S'的相對運動無關。