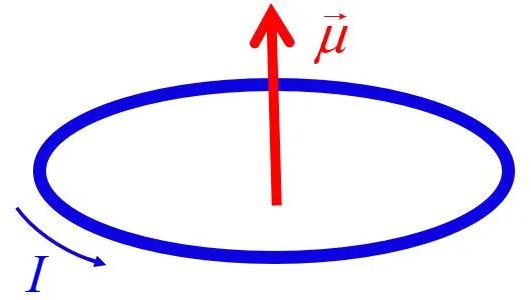
經典電動力學的基本規律是透過麥克斯韋方程組來描述的,若不考慮三個介質關係,共包含四個方程。
很多人覺得這四個方程看起來好複雜,但事實上,只要你抓住了其中的套路,你會發現,它們比你想象的簡單多了。
那麼,它們的套路是什麼?簡單的說,就是分別描述了電場和磁場的散度和旋度是什麼的問題。所以,只要你抓住了散度和旋度的概念,並理解了電場和磁場的源和旋,所有困難都將煙消雲散。
下面,我們先將方程逐個講一遍,然後再較詳細的闡述一下,對應電場和磁場,源和旋分別是什麼。
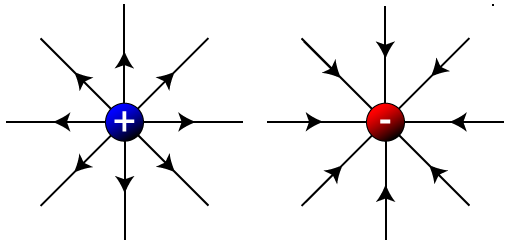
第一個方程是電場的高斯定理。
它給出電場與電荷之間的關係。電荷是電場中靜電場部分的源,對於感生電場來說,它是有旋的,它的場線是閉合的曲線,不對任何閉合曲面形成通量,是無源場。
按照高斯定理,場對閉合曲面的通量可以用它的散度對閉合曲面內的體積積分來代替,故有 這就是電場的高斯定理的微分形式。它表明,靜電場是透過點電荷激發的,電荷密度是靜電場的散度,而點電荷是靜電場的源,靜電場是有源場。
第二個方程是電場的環路定理。 它給出電場的環量與磁場的變化之間的關係。 靜電場是保守場,它是電勢的負梯度,因此一定是沒有旋度的,所以靜電場的環路積分必定為零。但感生電場是由閉合的場線描繪的,它的旋度等於磁感應強度的時間變化率的負值。
根據斯托克斯定理,場對閉合路徑的環量可以用它的旋度對閉合路徑包圍的曲面的通量來代替,故有 這就是電場的環路定理的微分形式。它表明感生電場是變化的磁場激發的,磁感應強度的時間變化率是感生電場的旋度,感生電場是有旋場。
第三個方程是磁場的高斯定理。 這是麥克斯韋方程組中最簡單的方程。它表明磁場是無源場,所以它對任意閉合曲面都不產生通量,因為磁場從來都不是從某個地方冒出來的,無論是傳導電流、磁化電流還是位移電流激發的磁場,他們的場線都是閉合的曲線。
根據高斯定理,磁場的對任意閉合曲面的通量都為零,那說明磁場的散度為零,即
這就是磁場的高斯定理的微分形式。它表明磁感應強度沒有散度,磁場沒有源,是無源場。
最後一個方程是磁場的安培環路定理。 它描述磁場強度與傳導電流和位移電流的關係。傳導電流和位移電流一起構成磁場強度的旋度。凡是有電流出現的地方,必有磁場的旋渦。
根據斯托克斯定理,磁場強度的旋度就是傳導電流與位移電流之和,即 這就是磁場的安培環路定理的微分形式。 它表明磁場強度是傳導電流和位移電流激發的,傳導電流和位移電流一起構成磁場的旋度,磁場是有旋場。
四個積分形式的方程寫在一起為 四個微分形式的方程寫在一起為
積分形式與微分形式的方程組是等價的,但微分形式更清晰的描述了空間點的電場與磁場的規律。
根據上面第一個微分式,靜電場是有源場,它在某點的散度等於該點的電荷密度,那麼自然的,對沒有電荷的地方,靜電場的散度為零。換句話說,靜電場是有源場,但靜電場並非處處都有散度。
根據第二個微分式,電場也可能有旋度,但導致這個旋度的電場是電場中的一種特殊成分——感生電場,它是由變化的磁場激發的一種電場,它的旋度等於磁場的時間變化率的負值。
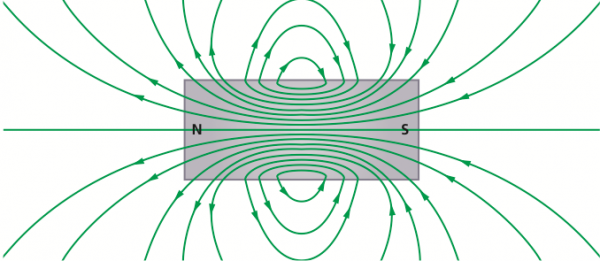
第三個微分式告訴我們,磁場一定是沒有散度的。意思是,磁場線永遠不會中斷,那麼它唯一的選擇是形成閉合曲線。例如一根條形磁鐵的磁感應線就是下面這個樣子,那些看起來沒有閉合的線只是因為太長而超出了圖片範圍罷了。
再看如下一個通電圓環的磁感應線分佈圖,那條水平線將閉合於無窮遠處。
由此可見,磁場線總是閉合的,它是無頭無尾、無始無終的,它不是從某個點被激發出來的!這一點也是磁與電的一個顯著的不同點,靜電場總是來自點電荷,電荷是靜電場的源,可是磁場沒有這樣一個類似的對應者。
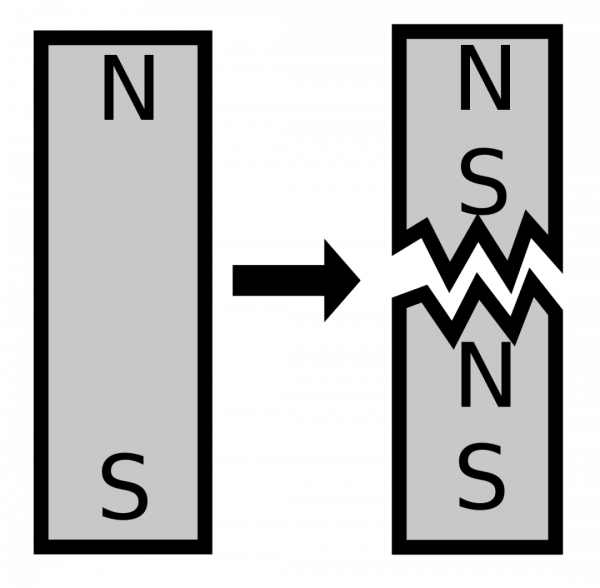
一根無論多短的磁鐵,總有兩個極:S極和N極。這種NS極永不分離的特性,決定了我們無法知道磁感應線到底從哪裡冒出來的。因為它從北到南,又從南到北,是一個閉環,沒有哪裡是起點,也沒有哪裡是終點,所以你找不到場的源!
實際上,這是由我們對於磁場的解釋決定的。電流導致磁矩,而磁矩導致磁場。磁矩對應的環形電流永遠有兩個面,所以它導致的磁場永遠有兩個極,就好比地球的軸的兩頭分別指向兩個相反方向一樣。
所以,你對“磁鐵的NS極永不分離”的疑問,與有人質疑“為什麼一張紙有兩面”、“一條線為什麼有兩端”是類似的。
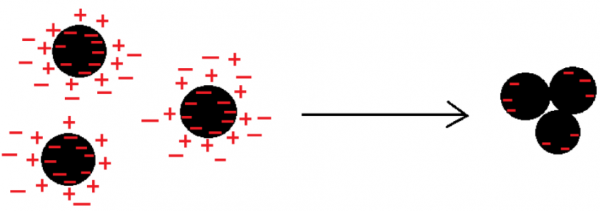
而電荷卻相反,異號電荷水火不容,等量的正負電荷相遇即中和!所以單獨存在的等量正負電荷是電場的源,但只要二者一合,源就消失了,也就不能激發電場了。
當然,你可能會說:不對!那電荷實際上還是分別位於電子和質子上,沒有中和啊!
你說得對!但既然這兩個等量正負電荷如此靠近,那麼在較大的觀察尺度上,我們可以認為,它們作為電場的正源和負源,彼此抵消了,包圍他們的曲面總體通量為零,整體對外不顯電性了!不能再對外激發電場了,這就是所謂的電荷已經被“中和”的證據。
當然,你可能聽說過磁單極子,如果哪天科學家真的找到單個存在的S極或N極,那麼磁場也將變為有源場,電磁理論將要被改寫。
第四個微分式告訴我們,磁場是有旋場,磁場強度在某點的旋度等於該點的電流密度和電位移向量的時間變化率之和。那麼,對沒有電流和電位移向量的時間變化率的點,磁場強度也沒有旋度。所以,磁場是有旋場,但不代表處處都有旋度。
由於經典電動力學是宏觀電磁學規律,因此上述描述中所謂的“點”是侷限在經典電磁學範圍內的點,不是真正意義上的無限小的點!實際上,這些點的尺寸遠遠比微觀粒子要大得多!
當涉及微觀粒子的電磁相互作用時,必須採用量子化的電動力學理論,它就是由費曼、施溫格和朝永振一郎等人於上世紀40年代前後創立的量子電動力學。
END
轉載內容僅代表作者觀點
不代表中科院物理所立場
來源:大學物理學
編輯:藏痴